| Aus Gründen der besseren Lesbarkeit wird im Folgenden die Sprachform des generischen Maskulinums
verwendet. Es wird an dieser Stelle darauf hingewiesen, dass die ausschließliche Verwendung der männlichen Form geschlechtsunabhängig
verstanden werden soll. |

(Quelle: https://pixabay.com/de/photos/albert-einstein-porträt-1144965/,
https://commons.wikimedia.org/wiki/File:
Albert_Einstein_signature_1934.svg, 29.08.2020) |
"Wenn man etwas
nicht einfach erklären kann,
hat man es nicht verstanden."

|
1. Die Newtonsche Mechanik
Ende des 19. Jahrhunderts waren viele Physiker davon überzeugt, dass alle wesentlichen Gesetze der
Physik bereits entdeckt sind und nur noch Details ausgearbeitet werden müssen. Mit Hilfe der Newtonschen Mechanik und der
Maxwellschen Feldtheorie konnte man die damals bekannten Erscheinungen in der Physik erklären.

Sir Isaac Newton (1642 – 1727)
(Quelle: "Sir Isaac Newton" by aldoaldoz is licensed under CC BY-NC-SA 2.0,
https://search.creativecommons.org/photos/dccf4c2a-b8b5-49f6-93d7-e084c7ade50d, 28.08.2020) |
|

(Quelle "Principia Philosophiae Naturalis Principia Mathematica, Title page" by CRC, University of Edinburgh is licensed under
CC BY-NC-SA 2.0, https://search.creativecommons.org/photos/7a0332da-0e10-403c-a7ea-4088456da2a3, 28.08.2020) |
In seinem Hauptwerk
"Philosophiae naturalis principia mathematica" geht der englische Naturforscher
Sir Isaac Newton von einem absoluten Raum und einer absoluten Zeit aus. Beide existieren objektiv. Raum und Zeit werden vom physikalischen
Geschehen nicht beeinflusst. Die Länge von Strecken und die Zeitdauer von Abläufen hängen damit nicht vom Bezugssystem des Beobachters
ab.
| |
"... der absolute Raum, seiner Natur nach ohne Beziehung zu etwas
Äußerem, bleibt immer gleich und unbeweglich ... die absolute, wahre und mathematische Zeit, in sich und ihrer Natur nach ohne Beziehung zu
irgendetwas Äußerem, fließt gleichmäßig dahin ..." |
|
Newton hat auf dieser Basis seine drei Grundgesetze der Mechanik aufgestellt.
1. Das Trägheitsgesetz
Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Bewegung auf gerader Bahn, solange
keine Kraft auf ihn einwirkt.
2. Das Dynamische Grundgesetz
Zur Beschleunigung a eines Körpers ist eine Kraft F
nötig. Diese ist proportional zur Masse m des Körpers und zur Beschleunigung a.

3. Das Wechselwirkungsgesetz
Kräfte treten immer paarweise auf. Sie sind gleich groß, aber entgegengesetzt gerichtet. Treten
zwei Körper in Wechselwirkung, so üben sie aufeinander gleich große, entgegengesetzt gerichtete Kräfte aus.
Für das obige Beispiel eines elastischen Stoßes bedeutet das

d.h. die beiden Körper erfahren gegengleiche Änderungen ihres Impulses.
2. Das Relativitätsprinzip der klassischen Mechanik -
Inertialsysteme
Wir betrachten zwei Bezugssysteme A und B.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020) |
 |
Im System A befindet sich ein Ball, der relativ zum Beobachter im System A in Ruhe ist. Für
diesen Beobachter gilt das Trägheitsgesetz: Der Ball bleibt in Ruhe, solange keine Kraft auf ihn einwirkt. Das System B bewegt sich mit
konstanter Geschwindigkeit am System A vorbei. Aus der Sicht des Beobachters im System B ist und bleibt der Ball in gleichförmiger
Bewegung, solange keine Kraft auf ihn einwirkt. Auch hier gilt das Trägheitsgesetz.
A und B bilden zwei gleichwertige Bezugssysteme, die sich relativ zueinander mit einer konstanten
Geschwindigkeit bewegen. In beiden gilt das Trägheitsgesetz (so wie alle anderen Gesetze der klassischen Mechanik).
Newton formulierte das Relativitätsprinzip der klassischen Mechanik so:
| |
"Die Bewegungen von Körpern in einem gegebenen Raum sind untereinander die
gleichen, ob sich der Raum in Ruhe befindet oder ob er sich konstant auf einer geraden Linie bewegt." |
|
Bezugssysteme, in denen das Trägheitsgesetz gilt, haben in der Physik eine besondere Bedeutung. Man
nennt sie Inertialsysteme (inertia (lat.) - Trägheit, Beharrungsvermögen, Ungeschicklichkeit). Alle Systeme, die relativ
zu einem Inertialsystem in Ruhe oder in gleichförmiger Bewegung sind, sind wieder Inertialsysteme.
Bewegt sich der Beobachter beschleunigt, so ist sein Bezugssystem im Allgemeinen kein Inertialsystem. So ist
z.B. ein rotierendes Bezugssystem kein Inertialsystem mehr. In der folgenden Animation (Ausschnitt aus einem Video) läuft eine Kugel entlang
einer Rinne auf eine rotierende Scheibe. Bewegt sich die Kugel nach Verlassen der Rinne aus der Sicht des "Labors" gleichförmig
geradlinig, so verläuft ihre Bewegung aus der Sicht einer mitrotierenden Kamera ohne erkennbare Kraft krummlinig d.h. beschleunigt. Das
Trägheitsgesetz gilt hier also nicht mehr.

(Quelle: Jodl, Hans-Jörg, IWF (Göttingen), Coriolis- und Zentrifugalkraft im rotierenden Bezugssystem, https://doi.org/10.3203/IWF/C-13095,
https://av.tib.eu/media/10796, 01.09.2020) |
 |

(Quelle: Icon von Icons8, https://icons8.de/icons/set/globus, 21.09.2020) |
 |
Streng genommen ist auch die Erde aufgrund ihrer Eigenrotation und ihrer gekrümmten
Bahnbewegung um die Sonne kein Inertialsystem. Und auch die Sonne bewegt sich mit ihren Planeten entlang einer gekrümmten Linie um das Zentrum
der Milchstraße. Für viele kurz andauernde Betrachtungen sind diese Abweichungen von einer geradlinigen Bahn allerdings
vernachlässigbar. Das beste Inertialsystem, von dem wir ausgehen können, ist der Fixsternhimmel. |
|
3. Die Lichtäther-Hypothese
Beugung, Interferenz und Polarisation von Licht zeigen, dass die Ausbreitung von Licht ein Wellenvorgang ist.
Die grundlegenden Vorstellungen dazu entwickelte der Holländer Christiaan Huygens.

(Quelle: "File:Diffraction Pattern White LED Light.jpg" by Laurie is licensed under CC BY 4.0,
https://search.creativecommons.org/photos/72a3ca9b-9ee4-4ba2-aa0f-4c271d25a85d, 02.09.2020) |

Christiaan Huygens (1629 – 1695)
(Quelle: "Christiaan Huygens by Caspar Netscher 1671, oil painting, Museum Boerhaave, Leiden" by koopmanrob is
licensed under CC BY-SA 2.0, https://search.creativecommons.org/photos/717d6b04-9294-4bcf-b388-9c2f121a80a9, 02.09.2020) |
Die Ausbreitung einer Welle ohne entsprechendes Medium war im mechanistischen Weltbild Ende des
19. Jahrhunderts nicht vorstellbar. Das Ausbreitungsmedium für Licht sollte nach den damaligen Vorstellungen der "Äther" sein. Der
Äther sollte alles durchdringen, das Innere der Atome ebenso wie den Raum zwischen den Galaxien. Die Vorstellung vom Äther ermöglichte
es, die Vorgänge der Optik mechanistisch zu deuten.
In der Ätherhypothese ist der gesamte Raum vom Äther erfüllt. Der Äther bildet das ruhende Bezugssystem des Universums, also ein
ausgezeichnetes Bezugssystem. Von jedem Objekt lässt sich eindeutig angeben, ob es bezüglich des Äthers in Ruhe oder in Bewegung ist.
Im Äther breitet sich Licht in alle Richtungen mit gleich großer Geschwindigkeit (der Lichtgeschwindigkeit) aus.
Dabei ergaben sich allerdings auch Probleme. Man musste dem Äther einander widersprechende Eigenschaften zugestehen. Nur Festkörper sind in
der Lage, Scherkräfte (Transversalkräfte) zu übertragen. Mechanische Transversalwellen können sich somit nur in
Festkörpern ausbreiten. Auch besteht ein Zusammenhang zwischen der Dichte des Ausbreitungsmediums und der Ausbreitungsgeschwindigkeit einer
Welle. Da die Lichtgeschwindigkeit sehr groß ist, müsste der Äther eine sehr große Dichte haben. Andererseits sollte der
Äther eine extrem kleine Dichte haben, da er sonst die Bewegung der Planeten merklich bremsen würde.
4. Das Michelson-Morley-Experiment
Das Ziel dieses Experiments war es, die Bewegung der Erde durch den Äther und damit gleichzeitig die
Existenz des Äthers nachzuweisen. Im Ruhsystem des Äthers breitet sich Licht in alle Richtungen mit gleich großer
Geschwindigkeit c aus. Die Erde bewegt sich mit der Geschwindigkeit v durch den Äther. Misst man auf ihr die
Ausbreitungsgeschwindigkeit des Lichts, so muss sich eine Richtungsabhängigkeit ergeben. In Bewegungsrichtung der Erde müsste sich der
kleinste, in entgegengesetzter Richtung der größte Wert ergeben.


(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 03.09.2020) |
 |
Die Geschwindigkeit der Erde ist im Vergleich zur Lichtgeschwindigkeit allerdings sehr klein. Um die daraus
resultierenden kleinen Laufzeitunterschiede eines Lichtstrahles messen zu können, ist höchste Präzision erforderlich. Der Amerikaner
Albert Abraham Michelson baute dazu ein Interferometer und führte 1881 in Potsdam und zusammen mit Edward Williams Morley
1887 mit einer verbesserten Anlage in Ohio entsprechende Messungen durch.

Albert Abraham Michelson (1852 – 1931, NP 1907)
(Quelle: https://commons.wikimedia.org/wiki/File:Albert_Abraham_Michelson.JPG, 03.09.2020) |

Edward Williams Morley (1838 – 1923)
(Quelle: https://commons.wikimedia.org/wiki/File:Edward_Williams_Morley2.jpg, 03.09.2020) |

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 04.09.2020)
Bewegt sich die Erde mit der Geschwindigkeit v durch den Äther, so sollten sich für die
Lichtwege 1236 und 1456 unterschiedliche Laufzeiten und damit
ein Interferenzmuster ergeben.

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 04.09.2020) |
 |

(Quelle: https://www.youtube.com/watch?v=87pPoGuLSuw, 01.09.2020) |
 |
 |
 |
| |
|
| Laufzeit 23 |
Laufzeit 45 |
| |
|
 |
 |
| |
|
| Wegen |
|
 |
| folgt für v < c |
|
 |
Die Messungen von Michelson und Morley konnten keine Relativbewegung zwischen Erde und Äther nachweisen.
Auch bei späteren Experimenten konnte kein Laufzeitunterschied zwischen den beiden, sich in unterschiedlicher Richtung ausbreitenden
Lichtstrahlen festgestellt werden.
Das wurde erwartet ...

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 04.09.2020) |
 |
Das wurde gemessen ...

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 04.09.2020) |
 |
5. Die Postulate Albert Einsteins

(Quelle: https://onlinelibrary.wiley.com/doi/pdf/10.1002/andp.19053221004, 07.09.2020) |

Albert Einstein (1879 – 1955, NP 1921)
(Quelle: https://commons.wikimedia.org/wiki/File:Einstein_patentoffice.jpg, 07.09.2020) |
Ausgehend von den erfolglosen Versuchen, die Existenz des Äthers nachzuweisen, stellte Einstein zwei
Postulate auf, die die Grundlage der Speziellen Relativitätstheorie darstellen.
| |
"Die misslungenen Versuche, eine Bewegung der Erde relativ zum "Lichtmedium" zu
konstatieren, führen zu der Vermutung, dass dem Begriff der absoluten Ruhe nicht nur in der Mechanik, sondern auch in der Elektrodynamik keine
Eigenschaften der Erscheinungen entsprechen ... Wir wollen diese Vermutung zur Voraussetzung erheben." |
|
1. Das Relativitätsprinzip
Es gibt kein ausgezeichnetes Inertialsystem, sondern alle Inertialsysteme sind gleichwertig. Physikalische
Vorgänge laufen in ihnen in der gleichen Weise ab, die physikalischen Gesetze haben in allen Inertialsystemen die gleiche Form.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-icon/flugzeug_2736761, https://www.flaticon.com/de/kostenloses-icon/apfel_123431, Icons erstellt von
Vectors Market, https://www.flaticon.com/de/kostenloses-icon/baum_740934, 25.09.2020) |
 |
2. Das Prinzip der Konstanz (Invarianz) der Vakuum-Lichtgeschwindigkeit
Die Vakuum-Lichtgeschwindigkeit ist konstant. Sie hat für alle Beobachter den gleichen Wert,
unabhängig davon, ob sich die Lichtquelle oder der Beobachter (oder beide) bewegen.
cvak = 299 792 458 m/s ≈ 300 000 km/s

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-icon/flugzeug_2736761, https://www.flaticon.com/de/kostenloses-icon/sonne_869767, 25.09.2020) |
 |
Aus diesen Postulaten ergeben sich Konsequenzen für die Messung von Raum und Zeit. Raum und Zeit sind in
der Speziellen Relativitätstheorie keine absoluten Größen, sondern hängen vom Bewegungszustand des Beobachters ab.
6. Die Zeitdilatation (Zeitdehnung)
Da nach den Postulaten der Speziellen Relativitätstheorie die Lichtgeschwindigkeit die einzige vom
Bewegungszustand des Systems unabhängige Größe ist, müssen wir alle Messungen auf die Ausbreitung des Lichts
zurückführen.
Die Idee der Lichtuhr
Die Zeiten in einem bewegten Bezugssystem und einem ruhenden Bezugssystem sollen mit Hilfe einer sogenannten
"Lichtuhr" genauer betrachtet werden.
 |
 |
Vom Boden einer Art Standzylinder geht ein Lichtsignal aus. Dieses läuft gleichförmig
zum oberen Ende des Zylinders, wo sich ein Spiegel befindet. Das Lichtsignal wird reflektiert und trifft wieder am Boden auf, wo es einen Zähler
weiterzählt. Ist der Standzylinder der Lichtuhr z.B. 15 cm hoch, so wird der Zähler jeweils nach 1 ns erhöht. |
|
Nun befindet sich die Lichtuhr in einem Zug, der mit großer, gleichbleibender Geschwindigkeit von links
nach rechts fährt.
Vom bewegten Beobachter aus gesehen ...

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 07.09.2020) |
 |
| |
|
(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 07.09.2020) |
 |
Für den bewegten Beobachter, der im selben Bezugssystem wie die Lichtuhr ist, ist die Sache einfach:
Für ihn läuft der Lichtstrahl immer senkrecht auf und ab. Ob der Zug steht oder mit konstanter Geschwindigkeit fährt, macht für
ihn in seinem Inertialsystem keinen Unterschied. Der Lichtstrahl bleibt immer "vor seiner Nase" und macht eine Bewegung zuerst aufwärts und dann
abwärts. (Man versuche mit den Augen des bewegten Beobachters zu sehen.)
Vom ruhenden Beobachter aus gesehen ...

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 07.09.2020) |
 |
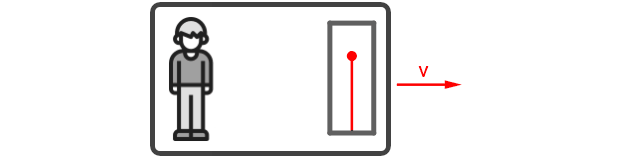
Der auf dem Bahnsteig stehende, ruhende Beobachter sieht etwas anderes, wenn der Zug mit der Lichtuhr mit
konstanter Geschwindigkeit an ihm vorbeifährt und er die Position des Lichtpunkts mit den Augen verfolgt. Für ihn durchläuft der
Lichtstrahl die rot eingezeichnete Bahn. Weil sich hier zwei gleichförmige Bewegungen überlagern, ist
die Bahn dreieckförmig.
Klassisches Modell (gleiche Zeitintervalle - unterschiedliche Lichtgeschwindigkeiten)
 |
Da der Zugwagen am ruhenden Beobachter mit konstanter Geschwindigkeit vorbeifährt, sieht
er den Lichtstrahl nicht senkrecht, sondern schräg nach oben laufen. Der Lichtstrahl muss also aus seiner Sicht eine längere Strecke
zurücklegen. Nach der Vorstellung der klassischen Physik mit einer absoluten Zeit wird zur Geschwindigkeit des Lichts die Geschwindigkeit des
Zugwagens vektoriell addiert. Der ruhende Beobachter würde für den Lichtstrahl im Zugwagen eine größere Geschwindigkeit
feststellen als der Beobachter im Zugwagen. Dies ist aber nach den Einsteinschen Postulaten nicht möglich. |
|
Relativistisches Modell (verschiedene Zeitintervalle - gleiche Lichtgeschwindigkeit)
 |
Da die zurückgelegten Strecken aus der Sicht der beiden Inertialsysteme verschieden lang
sind, die Ausbreitungsgeschwindigkeit des Lichts aber die gleiche ist, muss offensichtlich in beiden Systemen unterschiedlich viel Zeit vergangen
sein. |
|
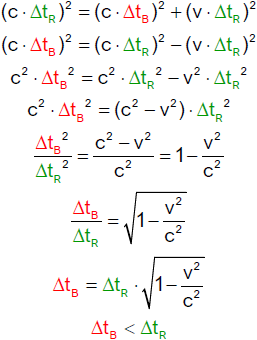
Vom ruhenden Beobachter aus gesehen vergeht auf der
bewegten Uhr weniger Zeit. Sie zeigt ein kleineres Zeitintervall an verglichen mit der Uhr des
ruhenden Beobachters.
Wir sagen: "Bewegte Uhren gehen langsamer, die Zeit wird
gedehnt."
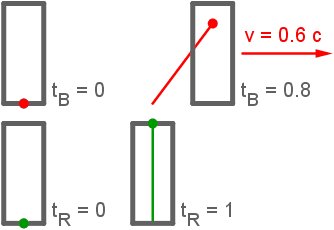 |
In der folgenden Animation gilt wegen v = 0.6 c

und damit

Wegen der Konstanz der Lichtgeschwindigkeit sind die rot bzw. grün gezeichneten Strecken in der linken
Abbildung gleich lang. |
|
"Zeitdehnung"
Nun kann jeder in einem Inertialsystem ablaufende Vorgang im weitesten Sinn als Uhr angesehen werden. Wir
können daher sagen:
| |
"Mit relativistischer Zeitdilatation bezeichnen wir jene Tatsache, dass ein
Beobachter für einen Vorgang, der an einem relativ zu ihm bewegten Ort stattfindet, ein größeres Zeitintervall misst als ein
Beobachter, der relativ zum Ort des Vorgangs ruht. Von allen relativ zueinander bewegten Beobachtern misst also derjenige für einen Vorgang das
kleinste Zeitintervall, der relativ zum Ort des Vorgangs ruht (Eigenzeit)." |
|

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von srip,
https://www.flaticon.com/de/kostenloses-icon/uhr_2344312, 11.09.2020)
Das Phänomen der Zeitdilatation ist wegen des Relativitätsprinzips ein "gegenseitiger" Effekt und
zeichnet keines der Bezugssysteme vor den anderen aus. Würde der Beobachter im Zug feststellen, dass die Uhr am Bahnsteig schneller geht, so
wäre das System "Bahnsteig" dadurch ausgezeichnet, dass in ihm die Uhr "absolut" (also für jeden Beobachter) schneller geht.
7. Nachweis der Zeitdilatation
Die Größenordnung der Zeitdilatation

Der Lorentz-Faktor k ist ein Maß für die Größenordnung der Zeitdilatation. Die
Gesetze der Relativitätstheorie gelten auch bei niedrigen Geschwindigkeiten. Allerdings zeigt der graphische Verlauf des Lorentz-Faktors, dass
die Zeitdilatation (wie auch die übrigen relativistischen Effekte) erst nahe der Lichtgeschwindigkeit groß wird.
 |
 |

(Quelle: "Marc Devis - 1965 Lola Chevrolet T70 Spyder 'Pussy Cat' at the 2016 Goodwood Revival (Photo 2)" by Dave Adams Automotive Images is
licensed under CC BY-NC-SA 2.0, https://search.creativecommons.org/photos/7008b570-c9ad-4a33-bd2b-63ecaf81c88d, 12.09.2020) |
Ein Auto mit einer Geschwindigkeit von 30 m/s (108 km/h) hat nur
ein Zehnmillionstel der Lichtgeschwindigkeit. Es muss ungefähr 6,3 Mio. Jahre ununterbrochen fahren, damit ein Zeitunterschied von
1 s entsteht. |
|

(Quelle: "Hamburg Airport: Austrian Airlines (OS / AUA) | Airbus A321-111 A321 | OE-LBC | MSN 0581" by kevin.hackert is
licensed under CC BY-NC 2.0, https://search.creativecommons.org/photos/74cb0d9d-a0ec-44e4-9552-b5b56d852fb7, 12.09.2020) |
Ein Flugzeug mit einer Geschwindigkeit von 300 m/s (1080 km/h) hat ein Millionstel der
Lichtgeschwindigkeit. Es muss ungefähr 63000 Jahre ununterbrochen fliegen, damit ein Zeitunterschied von 1 s
entsteht. |
|

(Quelle: NASA Ames Research Center, https://commons.wikimedia.org/wiki/File:Pioneer_10_Construction.jpg,
http://solarsystem.nasa.gov/multimedia/display.cfm?IM_ID=1586, 12.09.2020) |
Die schnellsten von Menschen gebauten Flugkörper sind interplanetare Sonden. Sie nützen zum
Teil die Gravitationswirkung der Planeten zur Beschleunigung aus und erreichen so bis zu 30 km/s. Das ist ein Zehntausendstel der
Lichtgeschwindigkeit. Sie müssen ungefähr 6,3 Jahre fliegen, damit ein Zeitunterschied von 1 s entsteht. |
|
Möchte man die Zeitdilatation also experimentell nachweisen, so benötigt man Uhren mit extrem hoher
Messgenauigkeit, oder man findet "Uhren", die sich mit fast Lichtgeschwindigkeit bewegen. Beides ist möglich.
Das Experiment von Hafele und Keating
Das erste und wohl berühmteste Experiment zur direkten Messung der Zeitdilatation wurde im
Herbst 1971 von Joseph Hafele von der Washington University (St. Louis, Missouri) und Richard Keating vom
U.S. Naval Observatory (Washington D.C.) durchgeführt. Die beiden Forscher transportierten vier Cäsium-Atomuhren in
Linienflügen einmal in westliche Richtung und einmal in östliche Richtung um die Erde und zeichneten dabei den Zeitverlauf auf. Nach einem
15 stündigen Flug wurden die Uhren mit jenen verglichen, die auf der Erde zurückgeblieben waren. Allerdings waren hier neben dem
Geschwindigkeitseinfluss auch die Einflüsse der Gravitation (Allgemeine Relativitätstheorie) zu berücksichtigen.

Joseph Hafele (links) und Richard Keating
(Quelle:
https://www.deutschlandfunk.de/einstein-auf-dem-pruefstand-9-wenn-atomuhren-in-die-luft.676.de.html?dram:article_id=326702, 11.09.2020) |

Eine der beim Experiment verwendeten Atomuhren, Typ HP 5061A
(Quelle: Binarysequence, Creative Commons Attribution-Share Alike 3.0 Unported,
https://commons.wikimedia.org/wiki/File:HP_5061A_Cesium_Beam_Frequency_Standard.JPG, 12.09.2020) |
Die folgende Tabelle zeigt die vorhergesagten (berechneten) und die tatsächlich gemessenen
Werte.


(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/flugzeug_2736761, 12.09.2020) |
 |
Die Animation simuliert das Haferle-Keating-Experiment. Zunächst gehen beide Uhren
gleich schnell. Nach dem Start geht die Uhr im Flugzeug (roter Zeiger) langsamer als die auf der Erde
verbliebene (grüner Zeiger). Nach der Landung gehen beide Uhren wieder gleich schnell, jedoch
bleibt der Gangunterschied erhalten. |
|
Heute müssen diese relativistischen Effekte beispielsweise in den Berechnungen des GPS
berücksichtigt werden.
Die Messung der Zeitdilatation mit Pionen (π+-Mesonen)
Pionen sind instabile Elementarteilchen. Man findet sie in der Höhenstrahlung, aber auch künstlich
erzeugt in Teilchenbeschleunigern. Die Halbwertszeit ruhender Pionen beträgt 18 ns. Nach dieser Zeit ist nur mehr die Hälfte der
ursprünglichen Pionen vorhanden. Die andere Hälfte ist in Myonen und Neutrinos zerfallen. Die Pionen erhalten dabei fast
Lichtgeschwindigkeit. Bei diesen Pionen ist eine Verlängerung ihrer Halbwertszeit festzustellen, da im System der (bewegten) Pionen die
Zeit langsamer vergeht.

Beispiel: v = 0.99 c

In einer Halbwertszeit zurückgelegte Strecke ...
... ohne Zeitdilatation:

... mit Zeitdilatation:

(Diese Strecke entspricht dem gemessenen Wert)
8. Die Längenkontraktion (Lorentz-Kontraktion)
Auch die Länge von Strecken hängt von der Relativbewegung der zu messenden Strecke bezüglich
des Beobachters ab.
Strecken in Bewegungsrichtung
Welche Strecke legt ein schneller "Zug" innerhalb einer Lichtsekunde zurück bzw. "wie lange ist der
Bahnsteig"?
Zur Messung der zurückgelegten Strecke benutzen wir die Lichtuhr im Zug, so wie wir sie von den
jeweiligen Bezugssystemen aus sehen.
Vom System "Bahnsteig" aus betrachtet ...

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 07.09.2020) |
 |
Vom System "Bahnsteig" aus betrachtet ist der Bahnsteig in Ruhe. Der Zug bewegt sich mit der
Geschwindigkeit v nach rechts, ebenso die Lichtuhr im Zug. Die Zeit, bis der Lichtpunkt wieder am unteren Rand ankommt, ist
ΔtR. Die vom Zug zurückgelegte Strecke (Länge des Bahnsteigs) ist
ΔsR = v · ΔtR.
Vom System "Zug" aus betrachtet ...

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 07.09.2020) |
 |
Vom System "Zug" aus betrachtet ist der Zug in Ruhe und in ihm auch die Lichtuhr. Der Bahnsteig bewegt sich
mit der Geschwindigkeit v nach links. Die Zeit, bis der Lichtpunkt wieder am unteren Rand ankommt, ist
ΔtB. Die vom Bahnsteig zurückgelegte Strecke (Länge des Bahnsteigs) ist
ΔsB = v · ΔtB.
Die Geschwindigkeit v, mit der sich die beiden Bezugssysteme relativ zueinander bewegen, ist für
beide Systeme vom Betrag her gleich. Da die Zeit ΔtR größer als
ΔtB ist, ist auch die Strecke ΔsR
größer als die Strecke ΔsB. Dabei gilt für den Zusammenhang zwischen
ΔtR und ΔtB:

Für die Längen gilt also

Bewegte Maßstäbe (Längen) werden in Bewegungsrichtung verkürzt gemessen. Man
spricht von Längenkontraktion.
Wir sagen: "Bewegte Maßstäbe schrumpfen."
oder korrekt formuliert
| |
"Mit relativistischer Längenkontraktion bezeichnen wir jene Tatsache, dass
für einen Beobachter die Länge eines relativ zu ihm bewegten Maßstabs in der Bewegungsrichtung kleiner ist als für einen
Beobachter, in dessen System der Maßstab ruht. Von allen relativ zueinander bewegten Beobachtern misst also derjenige für einen in der
Bewegungsrichtung liegenden Maßstab die größte Länge, der relativ zum Maßstab
ruht (Eigenlänge)." |
|
 |
Bewegt sich der Zug z.B. mit v = 0.6 c, so gilt
ΔsB = 0.8 · ΔsR.
Wenn wir vom Bahnsteig aus gesehen feststellen, der "Zug" ist
ΔsR = 100 m weit nach rechts gefahren, dann sagt der Beobachter im Zug, der
Bahnsteig hat sich um ΔsB = 80 m nach links bewegt. |
|
Ein "Planetensystem" ...
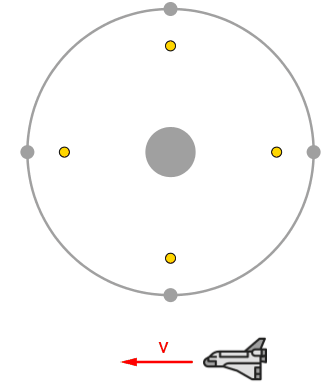
Ein "Planetensystem" bestehe aus einem Planeten und vier Raumstationen, die den Planeten im gleichen Abstand
umkreisen. Zu einem bestimmten Zeitpunkt wird vom Planeten zu jeder Station ein Lichtsignal gesendet und dort reflektiert. Ein Beobachter befindet
sich auf dem Planeten, ein zweiter in einem mit konstanter Geschwindigkeit vorbeifliegenden Raumschiff.
Für den Beobachter auf dem Planeten treffen die vier reflektierten Lichtsignale zum gleichen Zeitpunkt auf dem Planeten ein.
(Quelle: Icons erstellt von monkik, https://www.flaticon.com/de/kostenloses-icon/space-shuttle_1086134, 16.09.2020) |
 |
Für den Beobachter im Raumschiff ist das Raumschiff in Ruhe und das "Planetensystem" bewegt sich mit
konstanter Geschwindigkeit an ihm vorbei. Für ihn geraten die reflektierten Lichtsignale jedoch "außer Takt" und treffen nicht mehr zum
gleichen Zeitpunkt auf dem Planeten ein.

(Quelle: Icons erstellt von monkik, https://www.flaticon.com/de/kostenloses-icon/space-shuttle_1086134, 16.09.2020) |
 |
Nun kann jedoch die Art des Eintreffens der Signale nicht vom Bezugsystem des Beobachters abhängen.
Schließlich betrachten beide das gleiche Ereignis. Hier kann auch nicht mit der Relativität der Gleichzeitigkeit argumentiert werden, da
man sich in diesem Gedankenexperiment den Planeten auch als Punkt vorstellen kann und Raum-Zeit-Koinzidenzen nicht vom Inertialsystem
abhängen (vgl. Abschnitt 10). Betrachtet man die Wege, die die Lichtsignale zurücklegen, erkennt man, dass die horizontal laufenden
Signale eine größere Strecke zurücklegen müssen als die vertikal laufenden.
Für eine größere Strecke benötigt das Licht jedoch auch mehr Zeit. Gleiche Laufzeiten
ergeben sich nur dann, wenn der Raum in Bewegungsrichtung verkürzt wird.

(Quelle: Icons erstellt von monkik, https://www.flaticon.com/de/kostenloses-icon/space-shuttle_1086134, 16.09.2020) |
 |
Strecken quer zur Bewegungsrichtung
Strecken quer zur Bewegungsrichtung werden nicht verkürzt. Wäre dies so, dann würde für
einen Beobachter in einem "Zug", der auf einen Tunnel zurast, das Tunnelportal zu einem engen Nadelöhr schrumpfen, durch das der Zug niemals
passen würde. Ein ruhender Beobachter am Tunneleingang würde dagegen einen auf "Spielzeuggröße" geschrumpften Zug sehen und
hätte keinen Zweifel, dass der "locker durch die Tunnelröhre passt". Es darf natürlich nicht vom Beobachter abhängen, ob der Zug
durch den Tunnel kommt oder nicht.
Myonen in der kosmischen Höhenstrahlung
Myonen sind ein Hauptbestandteil der sekundären kosmischen Strahlung. Diese entsteht durch Reaktionen
der eigentlichen kosmischen Strahlung (vor allem aus dem Weltall kommenden Protonen) mit Atomkernen der oberen Atmosphäre in etwa
20 km Höhe. Myonen sind instabile Teilchen mit einer Halbwertszeit von ca. 2 µs und könnten nach den Gesetzen der
klassischen Physik kaum die Erdoberfläche erreichen. Dennoch registriert man hier einen beträchtlichen Myonenstrom.
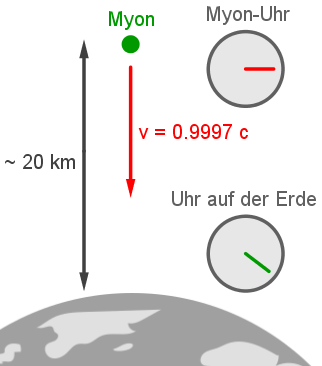
(Quelle: Icons erstellt von Vectors Market, https://www.flaticon.com/de/kostenloses-icon/globus_744480, 17.09.2020) |
Ein Beobachter auf der Erde erklärt dies damit, dass für die schnell bewegten
Myonen die Zeit langsamer vergeht als für ihn selbst (Zeitdilatation).

In einer Halbwertszeit zurückgelegte Strecke ...
... ohne Zeitdilatation
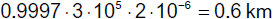
... mit Zeitdilatation

|
|

(Quelle: Icons erstellt von Vectors Market, https://www.flaticon.com/de/kostenloses-icon/globus_744480, 17.09.2020) |
Für die Myonen selbst vergeht in ihrem System die Zeit "normal". Die Erdoberfläche
kommt ihnen entgegen. Aufgrund der Lorentz-Kontraktion ist die Entfernung bis zur Erde jedoch "geschrumpft". Die Myonen können in ihrer
"normalen" Halbwertszeit die Erdoberfläche erreichen.

|
|
9. Wie wir relativistisch bewegte Objekte sehen
Früher nahm man an, dass sich schnell bewegte Objekte nur in Bewegungsrichtung
verkürzen (Lorentz-Kontraktion). So sollte ein Würfel als Quader und eine Kugel als Ellipsoid erscheinen.
(Quelle: Icons erstellt von monkik, https://www.flaticon.com/de/kostenloses-icon/radfahrer_1996882, 17.09.2020)
Das Bild, das in unserem Auge entsteht, wird jedoch durch jene Lichtstrahlen gebildet, die gleichzeitig im
Auge eintreffen. Diese Lichtstrahlen werden bei einem ausgedehnten Objekt jedoch von den einzelnen Punkten wegen der unterschiedlichen Laufzeit des
Lichts nicht gleichzeitig ausgesendet. Bei einem relativ zum Beobachter ruhenden Objekt ergibt sich kein Effekt. Bewegt sich jedoch ein Objekt mit
großer Geschwindigkeit relativ zum Beobachter, so erscheint es stark verzerrt, gekippt, gestreckt und verdreht. Die Tatsache der
Nicht-Beobachtbarkeit der Lorentz-Kontraktion ist als Penrose-Terrell-Effekt bekannt
Das "Sehen" ist somit streng von der Messung der Länge einer Strecke zu unterscheiden, wo Anfangs- und Endpunkt gleichzeitig bestimmt werden
müssen.
Die folgenden vier Animationen zeigen einen mit großer Geschwindigkeit bewegten Maßstab und das
Bild, das eine Kamera von diesem Maßstab festhält.

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |
Wie man die Rückseite eines schnell bewegten Würfels zu Gesicht bekommt ...

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |
Die Geschwindigkeit des Photons besitzt eine horizontale und eine vertikale Komponente. Wenn die
horizontale Komponente der Lichtgeschwindigkeit von der Geschwindigkeit v des Würfels übertroffen wird, kann das Photon "entkommen".
Der Würfel in der Animation bewegt sich mit 90 % der Lichtgeschwindigkeit und ist daher in Bewegungsrichtung auf 43,6 % seiner
Ruhlänge kontrahiert. |
|
Die folgende Animation zeigt die Bildentstehung bei einem vorbeifliegenden Würfel. Der Würfel wird
dabei als durchsichtig angenommen.

(Quelle: Icons erstellt von Smashicons, https://www.flaticon.com/de/kostenloses-icon/foto_2490093, 17.09.2020) |
 |
In der folgenden Abbildung sind einige Würfel in einer Reihe aufgestellt (unten). Eine zweite Reihe
Würfel bewegt sich mit 90 % der Lichtgeschwindigkeit über die ruhenden Würfel hinweg (oben, Bewegung von links nach rechts).
Alle Würfel, ruhende und bewegte, sind genau gleich ausgerichtet: Die Seite mit der "3" ist in Flugrichtung vorne, die Seite mit
der "4" hinten. Dass man von den bewegten Würfeln die Rückseiten mit der "4" sehen kann, ist eine Folge davon, dass sich Licht mit
einer endlichen Geschwindigkeit ausbreitet.

(Quelle: Ute Kraus, Institut für Physik, Universität Hildesheim, Tempolimit Lichtgeschwindigkeit,
https://www.tempolimit-lichtgeschwindigkeit.de/, cc-by-sa/2.0/de, 19.09.2020)
10. Die Relativität der Gleichzeitigkeit
Selbst so einfache alltägliche Aussagen wie "Diese beiden Ereignisse finden
gleichzeitig statt." müssen in der Relativitätstheorie hinterfragt werden.
Zwei Ereignisse, die in einem Inertialsystem am gleichen Ort stattfinden
Finden in einem Inertialsystem zwei Ereignisse am gleichen Ort gleichzeitig statt, so werden diese Ereignisse
auch von allen anderen Inertialsystemen als gleichzeitig beurteilt. Raum-Zeit-Koinzidenzen von Ereignissen hängen nicht vom Inertialsystem
ab.
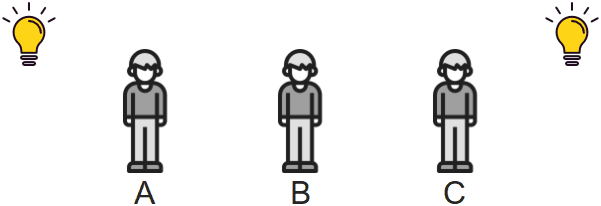
Zwei Ereignisse, die in einem Inertialsystem an verschiedenen Orten stattfinden
(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von
Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702814,
30.09.2020) |
 |
An zwei verschiedenen Orten leuchtet eine Lampe auf. Beobachter A sieht das linke Lichtsignal zuerst,
Beobachter C sieht das rechte Signal zuerst und Beobachter B - er befindet sich genau in der Mitte - sieht beide Lampen gleichzeitig
aufleuchten. Erklärbar ist dies mit der unterschiedlichen Laufzeit der Signale. Da Beobachter B beide Signale gleichzeitig sieht, geht er
davon aus, dass das Aufleuchten der Lampen gleichzeitig stattgefunden hat. Auch Beobachter A und Beobachter C werden, wenn sie die Laufzeit
der Signale berücksichtigen, zu diesem Ergebnis kommen. Die Gleichzeitigkeit von Ereignissen kann somit auch hier für alle gültig
beurteilt werden. Diese Erkenntnis nützt man zur Definition von Gleichzeitigkeit. Dabei wird wieder auf die konstante Lichtgeschwindigkeit
zurückgegriffen.
Definition der Gleichzeitigkeit
| |
Zwei Ereignisse, die an verschiedenen Orten im gleichen Inertialsystem stattfinden, sind
genau dann gleichzeitig, wenn von ihnen ausgehende Lichtsignale einen Beobachter in der Mitte gleichzeitig erreichen. |
|

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von
Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702814,
30.09.2020) |
 |
Zwei Ereignisse, die in relativ zueinander bewegten Inertialsystemen an verschiedenen Orten
stattfinden
In diesem Fall gibt es keine eindeutige Gleichzeitigkeit mehr. Wir betrachten dazu das Einsteinsche
Zugparadoxon.

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 30.09.2020)
Gegeben sind die beiden Inertialsysteme "Bahnsteig" (AB) und
"Wagen" (A'B'). Der Wagen bewegt sich relativ zum Bahnsteig mit konstanter Geschwindigkeit nach rechts. Zum
Zeitpunkt t = 0 (A = A' und
B = B') wird in der Mitte des Wagens ein Lichtblitz
gezündet.
Vom System "Bahnsteig" aus betrachtet ...

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797,
https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702814, 30.09.2020) |
 |
Der Wagen bewegt sich mit konstanter Geschwindigkeit nach rechts. Das Lichtsignal erreicht die
Punkte A und B gleichzeitig (diese sind gleich weit vom
Ursprung des Signals entfernt). Der Punkt B' hat sich während der Zeit, die das Signal zur Ausbreitung
benötigt, vom Lichtsignal wegbewegt. Der Punkt A' bewegt sich um die gleiche Strecke dem Signal
entgegen. Daher trifft das Signal - vom System "Bahnsteig" aus gesehen - zunächst im Punkt A' und dann
im Punkt B' ein.
Vom System "Wagen" aus betrachtet ...

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797,
https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702814, 30.09.2020) |
 |
Aus dieser Sichtweise ist der Wagen in Ruhe und der Bahnsteig bewegt sich mit konstanter Geschwindigkeit nach
links. Das Lichtsignal erreicht zuerst den Punkt B. Für einen Beobachter im Bezugsystem "Wagen"
bedeutet das, dass das Lichtsignal immer zuerst den Punkt B erreicht, egal wo er sich im Bezugssystem
befindet. Danach erreicht das Licht die Punkte A' und B'
gleichzeitig (unabhängig davon wo der Beobachter sich im Bezugsystem befindet). Schließlich erreicht das Licht den
Punkt A.
Wer hat Recht? Wie ist es möglich, dass von einem Bezugssystem aus gesehen
A und B gleichzeitig erreicht werden und im anderen
A' und B'? Es gibt keinen Grund, der einen oder der anderen Seite recht zu
geben. Die beiden Inertialsysteme sind gleichberechtigt. Es folgt vielmehr
Die Relativität der Gleichzeitigkeit
Es gibt keine absolute Gleichzeitigkeit zweier Ereignisse. Finden in einem Inertialsystem zwei Ereignisse an
verschiedenen Orten gleichzeitig statt, so finden diese Ereignisse in einem relativ dazu bewegten Inertialsystem zu verschiedenen Zeiten statt.
11. Scheinbare Überlichtgeschwindigkeit
Große Galaxien schleudern aus ihrem Zentrum Materieströme (Jets) mit hoher Geschwindigkeit in
den Raum. Bei in Richtung Erde orientierten Jets wurde mehrfache Lichtgeschwindigkeit gemessen. Dies ist aber nicht deren tatsächliche
Geschwindigkeit. Der Effekt kommt dadurch zustande, dass sich durch die Bewegung der Abstand zur Erde und damit auch die Laufzeit des Lichts
verkürzt.

Der 1918 entdeckte Jet von M87 entspringt dem aktiven Galaxienkern und erstreckt sich von dort mindestens 5000 Lichtjahre.
(Quelle: "M87 Jet" by gjdonatiello is marked with CC0 1.0,
https://search.creativecommons.org/photos/fd415d1b-cdb7-42c0-bd38-4fb408d5562e, 19.09.2020)
Ein Raumschiff ...

(Quelle: Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 19.09.2020)
Ein Raumschiff bewegt sich mit der Geschwindigkeit v = 0.75 c auf die Erde zu. In einer
Entfernung von 10 Lichtjahren sendet es ein grünes Lichtsignal aus.

(Quelle: Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 19.09.2020)
Nach 4 Jahren hat das Raumschiff eine Distanz von 3 Lichtjahren zurückgelegt und sendet ein
rotes Lichtsignal aus. Das grüne Signal ist noch
6 Lichtjahre von der Erde entfernt.

(Quelle: Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 19.09.2020)
Nach weiteren 6 Jahren erreicht das grüne Lichtsignal die
Erde. Wir sehen das Raumschiff in einer Entfernung von 10 Lichtjahren. Das rote Signal ist noch ein
Lichtjahr von der Erde entfernt.

(Quelle: Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 19.09.2020)
Ein Jahr später erreicht auch das rote Lichtsignal die Erde. Wir
sehen das Raumschiff in einer Entfernung von 7 Lichtjahren. Scheinbar hat das Raumschiff in einem Jahr die Distanz von 3 Lichtjahren
zurückgelegt.

(Quelle: Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490, 19.09.2020) |
 |
12. Die Galilei-Transformationen der klassischen Mechanik
In diesem Abschnitt wollen wir Transformationsgleichungen betrachten, mit denen
Raum- und Zeitkoordinaten eines Objekts oder eines Ereignisses von einem Inertialsystem in ein anderes Inertialsystem umgerechnet werden
können.
Die Galilei-Transformationen
Wir betrachten zwei Inertialsysteme S ( t , x , y , z ) und
S' ( t' , x' , y' , z' ). Das System S' bewegt sich relativ zu System S mit der konstanten
Geschwindigkeit v in Richtung +x. Für t = t' = 0 sollen die Achsen der beiden Systeme einander
überdecken (d.h. x-Achse ≡ x'-Achse, y-Achse ≡ y'-Achse und z-Achse ≡ z'-Achse).

(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/zylinder_1200865, 01.10.2020) |
 |
Wir erkennen unmittelbar
Bemerkung:
| • |
Da sich S' nur in x-Richtung bewegt, gilt y' = y und z' = z. |
| • |
Wegen der in der klassischen Physik existierenden absoluten Zeit gilt t' = t. |
| • |
Die Umkehrtransformation ergibt sich, wenn man gestrichene und ungestrichene Koordinaten vertauscht und v
durch −v ersetzt (S bewegt sich bezüglich S' in Richtung −x'). |
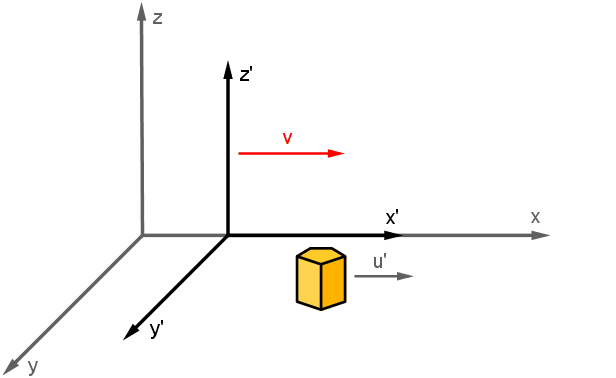
Die Geschwindigkeitsaddition der klassischen Mechanik
Wir betrachten wieder die beiden Inertialsysteme S und S' mit den obigen Voraussetzungen. Im
System S' bewegt sich ein Objekt mit der Geschwindigkeit u' in Richtung +x'. Welche Geschwindigkeit u besitzt dieses Objekt
bezüglich des Systems S?
(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/zylinder_1200865, 01.10.2020) |
 |
Wir müssen die Geschwindigkeit u' in das System S transformieren.

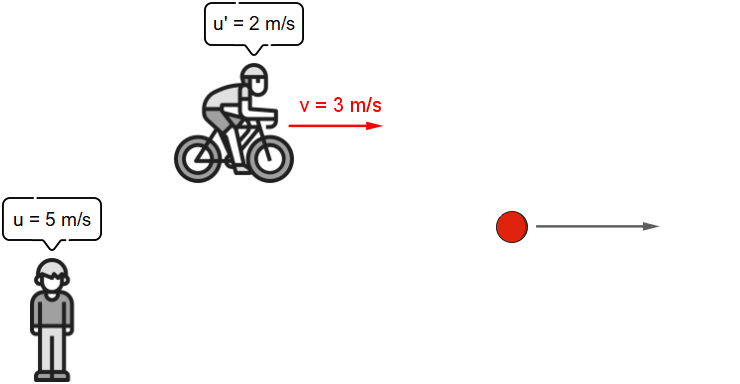
Das Ergebnis u = u' + v ist jenes, das wir aus unserer Erfahrung kennen und erwartet
haben.
(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, Icons erstellt von
monkik, https://www.flaticon.com/de/kostenloses-icon/radfahrer_1996882, Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-icon/sprechblase_2598839, https://www.flaticon.com/de/kostenloses-icon/kreis_594739, 03.10.2020) |
 |
Ein Problem tritt dann auf, wenn u' = c ist. Dann ist
u = c + v > c - ein Widerspruch zur Konstanz der Lichtgeschwindigkeit. Offensichtlich genügen die
Galilei-Transformationen nicht den Postulaten der Relativitätstheorie. Wir müssen die Transformationen daher modifizieren.
13. Die Lorentz-Transformationen

Hendrik Antoon Lorentz (1853 – 1928, NP 1902)
(Quelle: https://commons.wikimedia.org/wiki/File:H_A_Lorentz_(Nobel).jpg, 02.10.2020)
Bereits H. A. Lorentz war 1892 beim Versuch, das Michelson-Morley-Experiment zu erklären, auf diese
Transformationen gestoßen. Er war allerdings ein Anhänger der Ätherhypothese und erkannte die grundlegende Bedeutung dieser
Transformationen nicht.
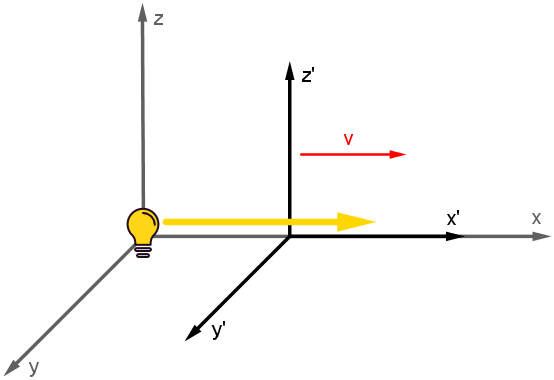
Wir betrachten zwei Inertialsysteme S ( t , x , y , z ) und
S' ( t' , x' , y' , z' ). Das System S' bewegt sich relativ zu System S mit der konstanten
Geschwindigkeit v in Richtung +x. Für t = t' = 0 sollen die Achsen der beiden Systeme einander
überdecken (d.h. x-Achse ≡ x'-Achse, y-Achse ≡ y'-Achse und z-Achse ≡ z'-Achse). Zum
Zeitpunkt t = t' = 0 wird
in ( 0 , 0 , 0 ) ≡ ( 0 , 0 , 0 )' ein Lichtsignal in Richtung +x
ausgesendet.
(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 30.09.2020)
Angenommen, es gibt einen Korrekturfaktor k, der den Fehler der Galilei-Transformationen ausgleicht,
dann gilt
 |
 |
(1) |
Wegen des Relativitätsprinzips muss der Faktor bei den Transformationen und den Umkehrtransformationen
der gleiche sein. Wegen der Konstanz der Lichtgeschwindigkeit muss gelten
 |
 |
(2) |
Die Herleitung des Korrekturfaktors
Einsetzen von (2) in (1) ergibt
Damit erhalten wir

Die Transformation der Zeit
Umformen der rechten Seite von (1) ergibt

Durch Einsetzen in die linke Seite von (1) und Auflösen nach t' erhalten wir

Damit erhalten wir die Lorentz-Transformationen
Für v ≥ c werden diese Transformationen physikalisch sinnlos (Division durch Null bzw.
Wurzel aus einer negativen Zahl). Die Relativgeschwindigkeit zweier Bezugssysteme und damit auch die Geschwindigkeit eines materiellen Objekts sind
somit stets kleiner als die Vakuumlichtgeschwindigkeit.
Eine besondere Darstellung der Lorentz-Transformationen
Multiplizieren wir die Gleichungen für die Transformation der Zeit mit c und setzen für das Produkt
c·t bzw. c·t' die Variable w bzw. w', so erhalten wir
Wir können w und w' auch in den Transformationen der x- bzw. x'-Koordinate verwenden.
Damit ergibt sich eine Darstellung der Lorentz-Transformationen, die die Symmetrie zwischen Zeit und Raum
besonders deutlich zeigt.
Das Zeitmaß w bzw. w' besitzt die Dimension einer Länge. Wenn wir sagen
w = 300 000 km, so ist dies gleichbedeutend mit t = 1 s.
Eine wichtige Identität

d.h.

Die Lorentz-Transformationen als Drehung in einem pseudoeuklidischen Raum
Betrachten wir zwei, um den Winkel α gegeneinander verdrehte kartesische Koordinatensysteme
K ( x , y ) und K' ( x' , y' ) mit identischem Koordinatenursprung O.

Für den Abstand d eines beliebigen Punktes P zum Koordinatenursprung O gilt nach dem Satz
von Pythagoras

Der Abstand eines Punktes P zum Ursprung O ändert sich bei Drehungen des Koordinatensystems um
den Ursprung also nicht – er ist invariant. Dabei gilt folgender Zusammenhang zwischen den Koordinaten des Punktes P, wobei
α jener Winkel mit Vorzeichen ist, um den das System K' gegenüber dem System K verdreht ist.
 |
(3) |
Ist ein Abstand zweier Punkte durch den Satz von Pythagoras bestimmt, so heißt die Metrik (der
Abstand) Euklidsche Metrik. Im vorhergehenden Abschnitt haben wir die Identität

kennen gelernt. Durch sie ist ebenfalls eine Invariante festgelegt. Wir können nun fragen:
"Welche Transformationen lassen den 'Abstand' w2 − x2
unverändert?" w2 − x2 unterscheidet sich von der Euklidschen Metrik durch ein Minuszeichen. Wir
nennen eine solche Metrik pseudoeuklidisch.
Setzen wir a = w und b = i·x, dann gilt
a2 + b2 = w2 − x2 und wir können die Drehung anwenden. Eingesetzt
in (3) erhalten wir
 |
(4) |
Um den Winkel α zu bestimmen, müssen wir spezielle Werte einsetzen.
Dazu betrachten wir wieder die beiden Inertialsysteme S und S'. Vom System S' aus betrachtet bewegt
sich der Koordinatenursprung des Systems S (x = 0) mit der Geschwindigkeit v in Richtung −x'. Für t' = 1
bzw. w' = c gilt für den Koordinatenursprung von S aus Sicht des Systems S' x' = −v. Setzen wir diese Werte in die
zweite Gleichung von (4) ein, so erhalten wir

woraus

folgt. Wir verwenden die folgenden trigonometrischen Formeln.
Es gilt daher
Einsetzen dieser beiden Beziehungen in (4) ergibt

und damit die Lorentz-Transformationen

Ergänzen wir die Identität

durch die y- und z-Koordinaten, so erhalten wir

und damit einen vierdimensionalen Raum mit einer pseudoeuklidischen Metrik, den sogenannten Minkowski-Raum,
benannt nach Hermann Minkowski, in dem sich die Relativitätstheorie besonders elegant formulieren lässt. Dieser vierdimensionale Raum
heißt auch Raumzeit oder das Raum-Zeit-Kontinuum.
Albert Einstein soll dazu gesagt haben: "Seit die Mathematiker über
die Relativitätstheorie hergefallen sind, verstehe ich sie selbst nicht mehr."
14. Folgerungen aus den Lorentz-Transformationen
Wir beschränken uns auf eine Raumdimension und betrachten zwei
Inertialsysteme S ( w , x ) und S' ( w' , x' ). Das System S' bewegt sich relativ zu
System S mit der konstanten Geschwindigkeit v in Richtung +x. Für w = w' = 0 sollen die Koordinatenursprünge
und die Raumachsen einander überdecken (d.h. x-Achse ≡ x'-Achse).
Die Zeitdilatation
Im System S' findet an einem festen Ort x' (d.h. x1' = x2')
ein Vorgang statt. Für diesen Vorgang misst der Beobachter im System S' die
Zeitdauer Δw' = w2' − w1'. Welche
Zeitdauer Δw = w2 − w1 misst der Beobachter in S für diesen in S' "ruhenden", d.h. an
einem relativ zu ihm bewegten Ort ablaufenden Vorgang?
Es gilt
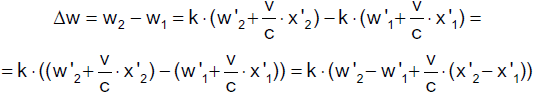
Nun ist x1' = x2', d.h.
x2' − x1' = 0. Daraus folgt

bzw.
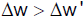
Der Beobachter im System S misst ein größeres Zeitintervall (Zeitdilatation).
Die Längenkontraktion
Im System S' ruht entlang der x'-Achse ein Maßstab. Für diesen Stab misst der Beobachter
in S' die Länge Δx' = x2' − x1'. Welche
Länge Δx = x2 − x1 misst der Beobachter im System S für diesen in S'
ruhenden, d.h. relativ zu ihm bewegten Stab? Der Beobachter in S muss dazu zu einem bestimmten Zeitpunkt w (d.h. gleichzeitig bzw.
w1 = w2) Anfangskoordinate x1 und Endkoordinate x2 des Stabes bestimmen.
Wir formen zunächst eine Gleichung aus den Lorentz-Transformationen geeignet um.

Dann gilt
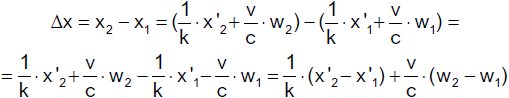
Nun ist w1 = w2, d.h.
w2 − w1 = 0. Damit erhalten wir

bzw.

Der Beobachter im System S misst eine kürzere Länge (Längenkontraktion).
Die Geschwindigkeitsaddition
Im System S' bewegt sich ein Objekt mit der Geschwindigkeit u' relativ zum Beobachter in S'. Welche
Geschwindigkeit u stellt der Beobachter im System S für dieses Objekt fest?
Es gilt:
 |
bzw. |
 |
Aus den Lorentz-Transformationen folgt

Damit erhalten wir das Ergebnis

Für u' und v sehr klein gegenüber der Lichtgeschwindigkeit ist der Nenner ≈ 1,
sodass wir das klassische Resultat erhalten. Für Geschwindigkeiten nahe der Lichtgeschwindigkeit ist diese Form der Geschwindigkeitsaddition zu
verwenden.
Einige Beispiele ...

(Quelle: Icons erstellt von ultimatearm, https://www.flaticon.com/de/kostenloses-icon/flugzeug_2855988, Icons erstellt von
Icongeek26, https://www.flaticon.com/de/kostenloses-icon/jet_3455083, 03.10.2020) |
 |

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/raumschiff_784923,
https://www.flaticon.com/de/kostenloses-icon/raumschiff_784925, 03.10.2020) |
 |

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/raumschiff_784925, Icons erstellt von
Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797, 03.10.2020) |

"Licht muss Licht bleiben" |
15. Die dynamische Masse
Durch Kräfte können Körper beschleunigt werden. Eine konstante Kraft F bewirkt bei
konstanter Masse m gemäß dem Dynamischen Grundgesetz F = m · a eine konstante Beschleunigung. Wegen
v = a · t hätte ein Körper nach genügend langer Zeit eine Geschwindigkeit größer als die
Lichtgeschwindigkeit. Dies ist jedoch aufgrund der Lorentz-Transformationen nicht möglich. Dann darf aber der Widerstand gegenüber
Beschleunigungen (Trägheit bzw. Masse eines Körpers) nicht konstant sein, sondern muss mit zunehmender Geschwindigkeit
größer werden.
Wir betrachten dazu das folgende Gedankenexperiment.
Zwei identische Massen mA und mB berühren jeweils ein Ende einer (ideal)
masselosen Spiralfeder, die mit einem an den Enden befestigten (ideal) masselosen Faden gespannt ist. mA und mB bilden
somit zusammen ein Massensystem, dessen Schwerpunkt S in der Mitte der Feder liegt. Beim Durchtrennen des Fadens werden die beiden Massen
zunächst kurzzeitig beschleunigt. Danach haben sie genau entgegengesetzt gerichtete, gleich große Geschwindigkeiten u bzw. −u
gegenüber dem Schwerpunkt S, der damit stets erhalten bleibt.
Ein mit der Masse mA mitbewegter Beobachter sieht dann, dass sich der Schwerpunkt S des
Systems mit der Geschwindigkeit u nach rechts bewegt. Die Masse mB bewegt sich relativ zum Schwerpunkt S mit der
Geschwindigkeit u nach rechts. mB bewegt sich daher relativ zu mA entsprechend der relativistischen
Geschwindigkeitsaddition mit der Geschwindigkeit
 |
(1) |
Daraus würde der mit der Masse mA mitbewegte Beobachter mit klassischer Mechanik
schließen, dass sich der Schwerpunkt S des Systems von der Mitte der Feder wegbewegt. Nach dem Relativitätsprinzip muss jedoch die
Beschreibung des Systems für alle Bezugssysteme konsistent sein. Der Schwerpunkt S kann nur dann für diesen Beobachter in der Mitte der
Feder bleiben, wenn die Masse von mB zunimmt. Betrachtet man das System zu einem bestimmten Zeitpunkt t, so ist der Abstand von
mA zum Schwerpunkt S gegeben durch LA = u · t. Der Abstand von mB zu mA
ist dann L = v · t. Somit ist der Abstand von mB zum Schwerpunkt gleich
LB = L − LA = (v − u) · t. Wenn auch für den mit der
Masse mA mitbewegten Beobachter der Schwerpunkt S des Systems in der Mitte der Feder bleiben soll, muss die folgende Beziehung
gelten.

Daraus folgt
 |
(2) |
Durch Quadrieren von (1) erhalten wir
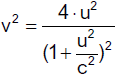 |
(3) |
Aus (2) und (3) ergibt sich

Daraus folgt

Ein in einem Inertialsystem mit der Geschwindigkeit v relativ zum Beobachter bewegter Körper
besitzt die dynamische Masse

Dabei ist m0 die Ruhemasse, also jene Masse, die der Körper in seinem Ruhsystem besitzt. Die
obige Gleichung zeigt, dass mit zunehmender Geschwindigkeit die dynamische Masse größer wird und bei Annäherung an die
Lichtgeschwindigkeit gegen unendlich geht. Kein Masseteilchen kann somit Lichtgeschwindigkeit erreichen, da dafür unendlich viel Energie
nötig wäre. Eine Ausnahme bilden nur Teilchen mit Ruhemasse 0 (Photonen). Die relativistische Massenzunahme zeigt sich bei
großen Teilchenbeschleunigern, wo die Magnetfelder, die die Teilchen auf ihrer Kreisbahn halten, wesentlich stärker sein müssen, als
nach der klassischen Physik zu erwarten ist.

(Quelle: "The Large Hadron Collider/ATLAS at CERN" by Image Editor is licensed under CC BY 2.0,
https://search.creativecommons.org/photos/23cd0a08-5d6b-4e4f-b97a-d1c31d26d9bd, 04.10.2020)

(Quelle: https://commons.wikimedia.org/wiki/File:FuerzaCentripetaLorentzN2.svg, 04.10.2020)
Die Ruhemasse eines Körpers ist eine sogenannte intrinsische Eigenschaft, d.h. sie haftet dem
Körper unmittelbar an, sie gehört (zu) ihm. Die dynamische Masse ist hingegen keine solche Eigenschaft, sondern eine Funktion der
Relativgeschwindigkeit gegenüber Körpern, die in anderen Bezugssystemen "ihre" eigene Ruhemasse haben. Sie ist keine Eigenschaft, die einem
Körper anhaftet, sondern Systemeigenschaft zweier Körper in einer Geschwindigkeitsbeziehung (Relativgeschwindigkeit). Genau genommen
kann also von einer dynamischen Masse eines betrachteten Körpers gar nicht gesprochen werden, denn für sich betrachtet hat er keine;
haben kann ein Körper nur eine Ruhemasse.
16. Masse - Energie - Impuls
Die Äquivalenz von Masse und Energie
Wird ein Körper beschleunigt, so wächst nicht nur seine Geschwindigkeit, sondern auch seine
dynamische Masse. Dabei kann dieser Massenzuwachs nur aus der für die Beschleunigung aufgewendeten Energie kommen. Wir betrachten die folgende
Ableitung.
Für |x| < 1 gilt die Formel

Daraus folgt

Multiplikation dieser Gleichung mit c2 ergibt

Der zweite Ausdruck auf der rechten Seite ist die klassische kinetische Energie. Da nur gleichartige
physikalische Größen addiert werden dürfen, muss somit auch m0 · c2 eine Energie sein. Sie
hängt nicht von der Geschwindigkeit ab. Es liegt nahe, sie als Ruhenergie zu bezeichnen, die ein Körper immer hat, auch wenn er sich nicht
bewegt. Daraus resultiert die berühmte Einstein-Formel, die die Äquivalenz von Energie und Masse ausdrückt.

Ändert sich die Energie eines Körpers um den Betrag ΔE, so ändert sich seine Masse um
den Betrag

Allerdings ist bei makroskopischen Objekten die Energie-Masse-Umwandlung sehr klein. In der Kern- und
Teilchenphysik spielt sie jedoch eine wichtige Rolle.

Friedrich Hasenöhrl (1874 – 1915)
(Quelle: https://commons.wikimedia.org/
wiki/File:Hasenoehrl.jpg, 05.10.2020) |
Schon vor der Veröffentlichung von Einsteins Relativitätstheorie im Jahre 1905 gab
es die Idee, dass Energie Masseeigenschaften besitzt. Anlass für diese frühe Einsicht waren unter anderem eine Erkenntnis des
österreichischen Physikers Friedrich Hasenöhrl, der bereits 1904 in den Annalen der Physik in seinem Aufsatz "Zur Theorie der Strahlung
bewegter Körper" ausführte, dass der Energie der Hohlraumstrahlung eine Masse m = E / c2 zuzuschreiben
ist. Dabei rechnete er ohne zusätzliche Annahmen nach der Maxwellschen Theorie. Bisweilen wird gegen Einstein der Vorwurf erhoben, den von
Hasenöhrl gefundenen Zusammenhang zwischen beiden Größen bei der Veröffentlichung seiner eigenen Energie-Masse-Beziehung nicht
erwähnt zu haben. Da beide Forscher in geringem zeitlichem Abstand im gleichen Wissenschaftsorgan publizierten, ist anzunehmen, dass Einstein
Hasenöhrls Arbeit kannte. |
|
Die Äquivalenz von Masse und Energie ist in Einsteins "Zur Elektrodynamik bewegter Körper" nicht
enthalten. Sie wurde von ihm einige Monate später in den
Annalen der Physik und Chemie, Jg. 18, S. 639 – 641, 1905 publiziert.

(Quelle: https://onlinelibrary.wiley.com/doi/pdf/10.1002/andp.19053231314, 04.10.2020)
Massendefekt und Paarbildung
Als Massendefekt (auch Massenverlust) bezeichnet man in der Kernphysik den Unterschied zwischen der
Summe der Massen aller Nukleonen (Protonen und Neutronen), aus denen ein Atomkern besteht, und der tatsächlich gemessenen (stets
kleineren) Masse des Atomkerns. Der Massenverlust kommt dadurch zustande, dass beim Zusammenschluss von Protonen und Neutronen zu einem Kern ein
kleiner Teil ihrer Massen in Energie umgewandelt und abgegeben wird. Diese Energie nennt man Bindungsenergie.
Die Masse eines Protons beträgt mp = 1,007276 Atomare Masseneinheiten (u), die eines Neutrons
mn = 1,008665 u. Der Kern von Helium 4He besteht aus zwei Protonen und zwei Neutronen; die Summe
aus deren Ruhemassen wäre 4,03188 u, die Ruhemasse des 4He-Kerns beträgt jedoch nur 4,00151 u. Der Massendefekt
beträgt hier also 0,03037 u beziehungsweise 0,76 % der Ausgangsmasse. Dies entspricht einer Energie von ca. 28 MeV.
Je größer bei einer Kernentstehung der Massendefekt ist, desto stärker sind die Kernteilchen aneinander gebunden. Messungen haben
ergeben, dass die Bindungsenergie pro Kernteilchen bei Kernen einzelner Elemente unterschiedlich ist und abgesehen von den sehr leichten Atomkernen je
Nukleon zwischen 7 MeV und fast 9 MeV liegt.

(Quelle: Ecodeluz, Creative Commons Attribution-Share Alike 4.0 International,
https://commons.wikimedia.org/wiki/File:Atomkernbindungsenergien_pro_Nukleon_Hippler_2016.png, 05.10.2020)
Die mittlere Bindungsenergie je Nukleon hat bei Kernen mit den Massenzahlen 40 bis 100 ihren
höchsten Wert und nimmt zu den leichteren und den schwereren Kernen hin ab. Dass die Bindung der Nukleonen bei den schweren Kernen lockerer wird,
ist darauf zurückzuführen, dass bei Vergrößerung der Nukleonenzahl die Kernkräfte insgesamt zwar zunehmen, aber eben nur
zwischen den benachbarten Teilchen wirken. Die abstoßenden Kräfte zwischen den Protonen nehmen ebenfalls zu, sie wirken aber zwischen allen
Protonen. Dadurch wird der Zusammenhalt zwischen den Kernteilchen wieder etwas gelockert.

(Quelle: "Amazing Hi-Def CME [full disk]" by NASA Goddard Photo and Video is licensed under CC BY 2.0,
https://search.creativecommons.org/photos/c2bdd467-4cc5-443e-af85-734db23c201d, 05.10.2020) |
Die Sonne "verbrennt" Wasserstoff zu Helium. Bei einer mittleren Leuchtkraft von
3.85 × 1026 W ergibt sich ein Massenverlust von 4.28 × 109 kg pro Sekunde,
was bei einer Gesamtmasse von 2 × 1030 kg nicht wirklich besorgniserregend ist. |
Unter Paarbildung versteht man in der Teilchenphysik die Bildung eines Teilchen-Antiteilchen-Paares. Dabei
muss die verfügbare Energie mindestens gleich der Summe der Ruhenergien der zu erzeugenden Teilchen sein, damit der Vorgang auftritt.
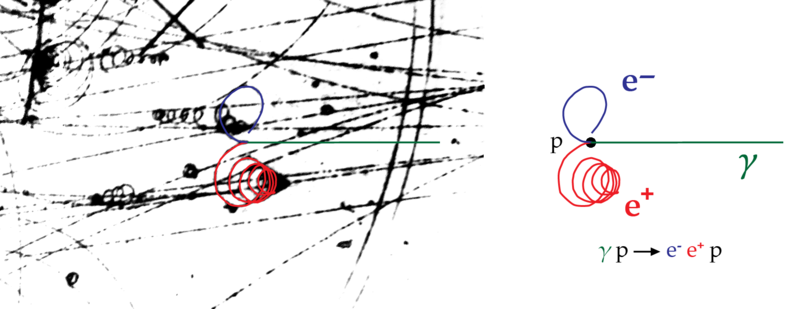
(Quelle: Ivan Baev, Creative Commons Attribution-Share Alike 3.0 Unported,
https://commons.wikimedia.org/wiki/File:Paarbildung_gamma_p_Desy_Blasenkammer_Rekonstruiert.png, 05.10.2020)
Die relativistische kinetische Energie
Betrachten wir nochmals die Gleichung

Sie kann gelesen werden als

Damit erhalten wir als Ausdruck für die kinetische Energie

Dieser Ausdruck stimmt für v << c mit dem Newtonschen Ausdruck für die kinetische
Energie überein.
Formt man die Gleichung

um zu

so ergibt sich daraus eine neue Interpretation für die dynamischen Masse eines Teilchens. Sie ist die
Ruhemasse - eine dem Teilchen anhaftende Eigenschaft (so wie z.B. die Ladung) - plus der Trägheit seiner kinetischen Energie.
Der relativistische Impuls
Analog zur klassischen Mechanik ist der Impuls gegeben durch

Für die Kraft erhält man

Die Gesamtenergie E kann wie folgt umgeformt werden.
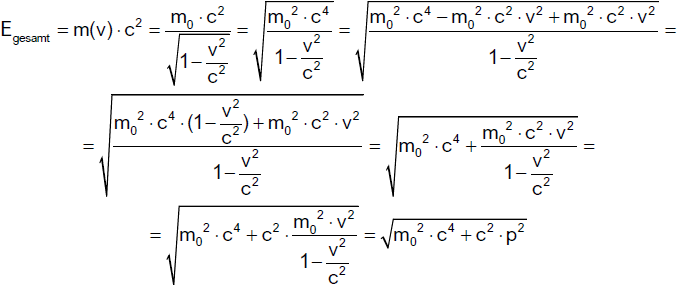
Dieses Resultat nennt man den relativistischen Energiesatz

17. Minkowski-Diagramme

Hermann Minkowski (1864 – 1909)
(Quelle: https://commons.wikimedia.org/wiki/
File:Hermann_Minkowski_Portrait.jpg, 05.10.2020) |
"Die Anschauungen über Raum und Zeit, die ich Ihnen
entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine radikale. Von
Stund' an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken und nur noch eine Art Union der beiden soll
Selbständigkeit bewahren."
Mit diesen Worten begann der deutsche Mathematiker Hermann Minkowski am 21. September 1908 vor der 80. Naturforscher-Versammlung
in Köln seinen Vortrag mit dem Titel "Raum und Zeit". Er entwickelte Diagramme, die es
ermöglichen, zwei relativ zueinander bewegte Inertialsysteme in einem Diagramm darzustellen und die Eigenschaften von Raum und Zeit in der
Speziellen Relativitätstheorie zu veranschaulichen. Dabei beschränkte er sich auf eine Raumdimension. |
|
Wir betrachten zwei Inertialsysteme S ( w , x ) und
S' ( w' , x' ). Das System S' bewegt sich relativ zu System S mit der konstanten Geschwindigkeit v in
Richtung +x. Für w = w' = 0 sollen die Koordinatenursprünge und die Raumachsen einander überdecken (d.h.
x-Achse ≡ x'-Achse). Wir nennen S das ruhende und S' das bewegte System. In jedem der beiden Systeme ruht im Koordinatenursprung
jeweils ein Beobachter.
Die Raum- und Zeitachse des ruhenden Systems S

Wir verwenden die waagrechte Achse für den Raum x und die senkrechte für die Zeit w.
Wegen der in der Relativitätstheorie auftretenden großen Geschwindigkeiten verwenden wir als Einheit
1 Lichtsekunde (Ls) = 299792458 m d.h. [ x ] = [ w ] = 1 Ls. Man beachte, dass
sowohl x als auch w die Dimension einer Länge besitzen und es dadurch gerechtfertigt ist, die Einheitspunkte auf den Achsen äquidistant vom
Ursprung aus aufzutragen.
Weltlinien

Unter einer Weltlinie verstehen wir den Weg eines punktförmigen Objekts durch Raum und Zeit. Die
Weltlinie a gehört zu einem Objekt, das sich bezüglich des Systems mit der Geschwindigkeit v = 0.33 c nach links
bewegt. Linie b entspricht einem Objekt, das mit v = 0.5 c nach rechts läuft. Ein nach rechts laufender Lichtstrahl besitzt
Linie c. Seine Weltlinie besitzt eine Steigung von 45°. Linie d gehört zu einem Objekt, das im System ruht. Da wir
ausschließlich gleichförmig bewegte Objekte betrachten, sind alle Weltlinien Geraden. Da kein materielles Objekt Lichtgeschwindigkeit
erreichen kann, muss jede Weltlinie mit der x-Achse einen Winkel größer als 45° einschließen.
Die Achsen des bewegten Systems S'

| Für die x'-Achse gilt w' = 0. Damit folgt aus den Lorentz-Transformationen |
|
Für die w'-Achse gilt x' = 0. Damit folgt aus den Lorentz-Transformationen |
 |
|
 |
Man beachte, dass die w'-Achse die Weltlinie des Beobachters im System S' bezüglich des
Systems S darstellt. Aufgrund des Relativitätsprinzips kann auch S' als das ruhende System angesehen werden. S bewegt sich dann mit der
Geschwindigkeit v in Richtung −x'. Das entsprechende Diagramm sieht wie folgt aus.

Die Einheitspunkte auf den Achsen des bewegten Systems S'

Zur Bestimmung der Einheitspunkte auf der w'- und der x'-Achse verwenden wir die Identität
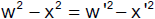
Für den Einheitspunkt auf der x'-Achse gilt x' = 1 und w' = 0, d.h.
 |
(1) |
Für den Einheitspunkt auf der w'-Achse gilt x' = 0 und w' = 1, d.h.
 |
(2) |
Die Kurven (1) und (2) sind Hyperbeln. Ihre Schnittpunkte mit der x'- bzw. w'-Achse ergeben
die Einheitspunkte auf den Achsen des Systems S'. Die Punkte ( 0 , 1 )' und ( 1 , 0 )' sind vom
Ursprung des Systems S' gleich weit entfernt, was für die Konstanz der Lichtgeschwindigkeit von Bedeutung ist.
Die Koordinaten eines Ereignisses bezüglich der Systeme S bzw. S'

Jedem Ereignis E können im jeweiligen Bezugssystem Orts- und Zeitkoordinaten zugewiesen werden.
Die Konstanz der Lichtgeschwindigkeit
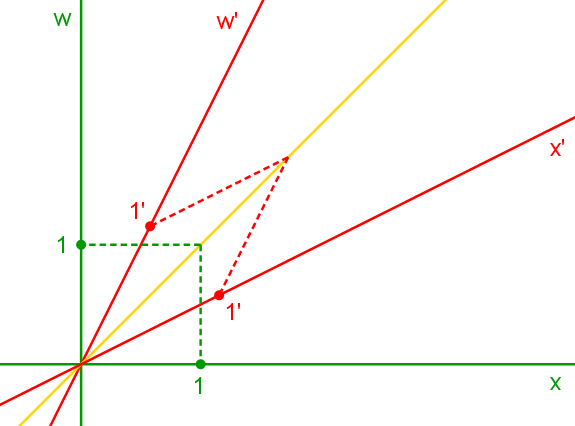
In den Systemen S bzw. S' gilt: Für Δw = 1 ist Δx = 1
bzw. für Δw' = 1 ist Δx' = 1.
Die Zeitdilatation
In jedem der beiden Systeme ruht im Ursprung eine Uhr. Für x = x' = 0 gilt
w = w' = 0.

Aus der Sicht des Beobachters im System S gilt: Zeigt die Uhr in S das
Zeitintervall Δw = 1, so zeigt die Uhr im System S' das Zeitintervall Δw' < 1.

Aus der Sicht des Beobachters im System S' gilt: Zeigt die Uhr in S' das
Zeitintervall Δw' = 1, so zeigt die Uhr im System S das Zeitintervall Δw < 1.
Die Längenkontraktion

Im System S' ruht entlang der x'-Achse ein Maßstab der Länge Δx' = 1.
Der Beobachter in S bestimmt zum Zeitpunkt w = 0 (also aus seiner Sicht gleichzeitig) Anfangs- und Endpunkt des Maßstabs und
stellt eine Länge Δx < 1 fest.

Im System S ruht entlang der x-Achse ein Maßstab der Länge Δx = 1. Der
Beobachter in S' bestimmt zum Zeitpunkt w' = 0 (also aus seiner Sicht gleichzeitig) Anfangs- und Endpunkt des Maßstabs und
stellt eine Länge Δx' < 1 fest.
Die Relativität der Gleichzeitigkeit

Die Ereignisse E1 und E2 finden im System S gleichzeitig statt. Für den
Beobachter in S' findet E1 nach E2 statt.

Die Ereignisse E1 und E2 finden im System S' gleichzeitig statt. Für den
Beobachter in S findet E1 vor E2 statt.
Die Synchronisation von Uhren

(Quelle: Icons erstellt von Good Ware, https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702797,
https://www.flaticon.com/de/kostenloses-icon/die-gluhbirne_702814, Icons erstellt von srip,
https://www.flaticon.com/de/kostenloses-icon/uhr_234431205.10.2020) |
 |
In den Systemen S und S' ruhen jeweils zwei Uhren - im System S bei x = 1 bzw.
x = −1 und im System S' bei x' = 1 bzw. x' = −1. Die beiden Beobachter wollen die Uhren gleichzeitig in
Gang setzen. Dazu werden zum Zeitpunkt w = w' = 0 in x = x' = 0 zwei Lichtsignale in Richtung
+x = +x' und −x = −x' ausgesendet.

Aus der Sicht des Beobachters im System S wird die Uhr −1' zuerst gestartet. Dann werden
gleichzeitig die Uhren in seinem System in Gang gesetzt. Als letzte Uhr wird 1' vom Lichtsignal erreicht. Er behauptet: Die Uhren im System S
gehen synchron, die Uhren im System S' nicht.

Aus der Sicht des Beobachters im System S', der sich ja als ruhend annehmen darf, wird die Uhr 1
zuerst gestartet. Dann werden gleichzeitig die Uhren in seinem System in Gang gesetzt. Als letzte Uhr wird −1 vom Lichtsignal erreicht. Er
behauptet: Die Uhren im System S' gehen synchron, die Uhren im System S nicht.
Raum- und zeitartige Ereignisse - Kausalität
Wir betrachten jetzt drei relativ zueinander bewegte Inertialsysteme S ( x , w ),
S' ( x' , w' ) und S'' ( x'' , w'' ). Für w = w' = w'' = 0 ist
x = x' = x'' = 0. Außerdem sind das Ereignis O - es findet in jedem der drei Systeme zum
Zeitpunkt w = w' = w'' = 0 im Ursprung statt - und ein weiteres Ereignis E gegeben.

Die Ereignisse O und E finden im System S gleichzeitig statt. Aus Sicht des Systems S' findet
das Ereignis E vor dem Ereignis O statt, im System S'' ereignet sich E jedoch nach O. Es gibt also für die Ereignisse O und E
keine eindeutige zeitliche Abfolge. Die Ereignisse können einander daher auch nicht beeinflussen. Jedoch haben in jedem der drei Systeme die
beiden Ereignisse verschiedene Ortskoordinaten. Wir sagen: "Die Ereignisse O und E sind nicht durch die Zeit
jedoch durch den Raum getrennt." Wir nennen sie daher raumartige Ereignisse.

In der obigen Abbildung finden die Ereignisse O und E bezüglich des Systems S am gleichen Ort
statt. Vom System S' bzw. S'' aus betrachtet besitzen O und E verschiedene Ortskoordinaten. Jedoch ereignet sich in jedem der drei Systeme E
vor O, d.h. es gibt in jedem System die gleiche eindeutige zeitliche Abfolge der beiden Ereignisse. Das Ereignis E kann das Ereignis O
beeinflussen. Wir sagen: "Die Ereignisse O und E sind nicht durch den Raum jedoch durch die Zeit
getrennt." Wir nennen sie daher zeitartige Ereignisse.
Auch in der folgenden Abbildung sind O und E zeitartige Ereignisse, jedoch findet E in allen drei Systemen nach O statt.

Die folgende Abbildung zeigt den sogenannten "Lichtkegel" des Ereignisses O.

Alle Ereignisse im Bereich 1 sind raumartige Ereignisse bezüglich O. Sie können das
Ereignis O nicht beeinflussen bzw. vom Ereignis O beeinflusst werden. Wir nennen diesen Bereich die
"Gegenwart" von O.
Ereignisse im Bereich 2 finden für alle Beobachter vor dem Ereignis O statt. Diese Ereignisse können das Ereignis O
beeinflussen. Wir nennen diesen Bereich die "Vergangenheit" von O.
Ereignisse im Bereich 3 finden für alle Beobachter nach dem Ereignis O statt. Diese Ereignisse können von O beeinflusst werden.
Wir nennen diesen Bereich die "Zukunft" von O.
18. Paradoxa
Schon früh wurden Gedankenexperimente ersonnen, um die eine oder andere Lücke in der Speziellen
Relativitätstheorie durch scheinbare Widersprüche aufzudecken (altgriechisch
παράδοξος "wider Erwarten, wider die gewöhnliche Meinung, unerwartet, unglaublich").
Das Leiter-Garagen-Paradoxon
Gegeben sei eine Garage mit zwei offenen Türen und eine Leiter, die sich mit konstanter
Geschwindigkeit v auf die Garage zubewegt. Sobald die Leiter vollständig in der Garage ist, werden beide Türen gleichzeitig geschlossen
und augenblicklich wieder geöffnet, um der Leiter ein Passieren der Garage zu ermöglichen. Klassisch betrachtet ist dies natürlich nur
möglich, wenn die Länge der Leiter kleiner oder höchstens gleich der Länge der Garage ist.
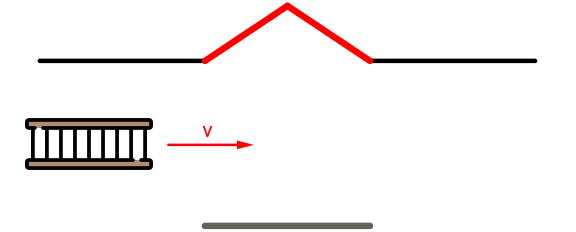
(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/leiter_517599, 07.10.2020) |
 |
Im Folgenden sei die Ruhlänge der Leiter größer als die Ruhlänge der Garage. Ist es
möglich, dass die Leiter unter diesen Bedingungen in die Garage passt?

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/leiter_517599, 07.10.2020)
Vom "Garagen"-System aus gesehen ...
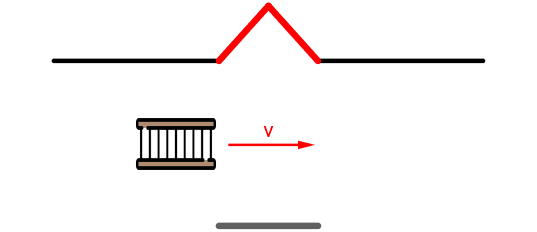
Aus Sicht eines Inertialsystems, in dem die Garage ruht, ist die Leiter in Bewegung, und aufgrund der
Längenkontraktion kann die Leiter durch Wahl einer passenden Geschwindigkeit so kurz gemacht werden, dass sie in die Garage passt.
(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/leiter_517599, 07.10.2020) |
 |
Vom "Leiter"-System aus gesehen ...
Hier ist die Garage aus Sicht des Systems der Leiter bewegt und folglich kontrahiert. Aus dieser Perspektive
ist die Garage kleiner und die Leiter kann unmöglich in die Garage passen. Dass diese Situation nicht zu einem Widerspruch führt, liegt an
der Relativität der Gleichzeitigkeit, d.h. was ein Beobachter im "Garagensystem" als gleichzeitig wahrnimmt, ist nicht gleichzeitig für
einen Beobachter im "Leitersystem". Das zugehörige Minkowski-Diagramm zeigt dies.
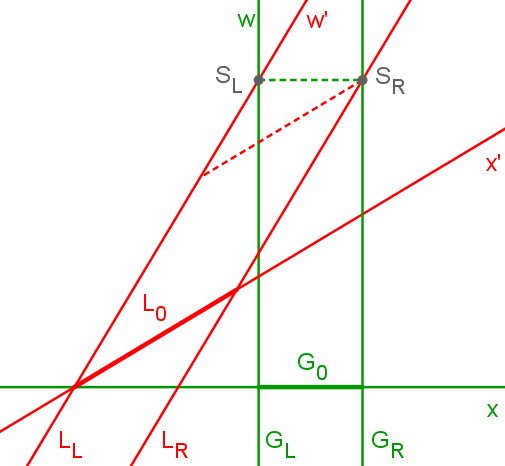
Das Diagramm zeigt das Ruhsystem der
Garage S ( w , x ) und das dazu relativ bewegte Ruhsystem der
Leiter S' ( w' , x' ). G0 ist die
Ruhlänge der Garage, L0 die Ruhlänge der Leiter.
GL und GR bezeichnen die Weltlinien des linken und
rechten Endes der Garage, LL und LR die Weltlinien des
linken und rechten Endes der Leiter. Aus Sicht der Garage finden die Ereignisse SL (Schließen der linken Tür) und
SR (Schließen der rechten Tür) gleichzeitig statt. Im "Leitersystem" wird jedoch die rechte Tür vor der linken
Tür geschlossen, sodass auch hier die Leiter in die Garage passt.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/leiter_517599, 07.10.2020) |
 |
Das Zwillings- bzw. Uhren-Paradoxon
In diesem Gedankenexperiment fliegt ein Zwilling in einem Raumschiff mit nahezu Lichtgeschwindigkeit zu einem
weit entfernten Stern, während der andere Zwilling auf der Erde zurückbleibt. Anschließend kehrt der reisende Zwilling mit der
gleichen Geschwindigkeit wieder zurück. Nach der Rückkehr zur Erde stellt sich heraus, dass der dort zurückgebliebene Zwilling
älter ist als der gereiste. Dies ist eine Folge der Zeitdilatation.

(Quelle: Icons erstellt von monkik, https://www.flaticon.com/de/kostenloses-icon/junge_701995,
https://www.flaticon.com/de/kostenloses-icon/frau_701989, https://www.flaticon.com/de/kostenloses-icon/mann_702004, 10.10.2020)

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490,
Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881, 12.10.2020) |
 |
Die Zeitdilatation selbst ist gemäß dem Relativitätsprinzip ein symmetrischer Effekt. Das
heißt, jeder der beiden Zwillinge muss die Uhr des anderen als bewegt und somit deren Gang als verlangsamt betrachten können. Der gereiste
Zwilling könnte also behaupten, nicht er, sondern die Erde hat sich bewegt und daher ist der auf Erde verbliebene Zwilling jünger
geblieben.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/planet-erde_921490,
Icons erstellt von Nikita Golubev, https://www.flaticon.com/de/kostenloses-icon/raumschiff_290881, 12.10.2020) |
 |
Es ergibt sich somit die Frage, warum die auf der Erde verbliebene Uhr nicht aus Sicht der
zurückkehrenden Uhr beim Zusammentreffen nachgeht. Das würde einen Widerspruch ergeben, denn beim Zusammentreffen können die beiden
Uhren nicht jeweils gegenüber der anderen nachgehen.
Das Paradoxon beruht auf der unzulässigen Annahme über die Symmetrie der beiden Standpunkte. Insbesondere wird dabei der Richtungswechsel am
Umkehrpunkt der Reise des Zwillings ignoriert. Dieser Richtungswechsel ist für den reisenden Zwilling als Beschleunigung spürbar. Damit der
reisende Zwilling sich während der Hin- und Rückreise in einem Inertialsystem befindet, muss er im Moment der Richtungsumkehr sein
Bezugssystem wechseln. Für den anderen, auf der Erde verweilenden Zwilling ändert sich durch die Richtungsumkehr des reisenden Zwillings
hingegen nichts - er verbleibt in seinem Inertialsystem.
Korrekterweise müssen wir also drei Bezugsysteme betrachten, wie das folgende Minkowski-Diagramm zeigt. Für das Raumschiff wurde dabei die
Geschwindigkeit v = 0.6 c angenommen, sodass der Faktor für die Zeitdilatation und die Längenkontraktion 0.8
beträgt. Das Ziel des reisenden Zwillings liegt 3 Lichtjahre von der Erde entfernt.

Im obigen Diagramm sind die Weltlinien der Uhr auf der
Erde (grün) und jener im Raumschiff (rot) eingezeichnet.
Die strichlierten roten Linien sind Linien der Gleichzeitigkeit aus der Sicht des Raumschiffs (Parallele zur
Raumachse des jeweiligen Bezugssystems) und beantworten für den reisenden Zwilling die Frage: "Wie spät
ist es jetzt auf der Erde?"
Aus der Sicht des Zwillings auf der Erde sind für den Hin- und Rückflug jeweils 5 Jahre nötig. Aus seiner Sicht ist der reisende
Zwilling nur um jeweils 5 · 0.8 = 4 Jahre gealtert. Der reisende Zwilling erklärt seinen geringeren Zeitbedarf
damit, dass sich die Entfernung zum Reiseziel wegen der Längenkontraktion auf 3 · 0.8 = 2.4 Lichtjahre
verkürzt hat.
Da aus seiner Sicht die Zeit auf der Erde langsamer vergeht als im Raumschiff, scheinen auf der Erde unmittelbar vor seiner Ankunft auf dem Stern erst
4 · 0.8 = 3.2 Jahre vergangen zu sein. Aus der Sicht des Zwillings auf der Erde tritt das Ereignis der Ankunft auf dem
Stern jedoch erst 1.8 Jahre später ein.
Durch den Wechsel des Inertialsystems während der Umkehrphase verschiebt sich aber jetzt die Wahrnehmung des reisenden Zwillings bezüglich
des auf der Erde "gleichzeitigen" Ereignisses um 3.6 Jahre und löst dadurch den Widerspruch auf. Die durch die schwarze Strecke
gekennzeichneten Ereignisse auf der Erde treten also niemals im "Jetzt" des reisenden Zwillings auf.
Zusammen mit weiteren 3.2 Jahren auf dem Rückweg sind also auch aus der Sicht des reisenden Zwillings auf der Erde insgesamt 10 Jahre
vergangen, während er selbst nur 8 Jahre älter geworden ist.
Literatur:
Höfling, Oskar: Physik - Lehrbuch für Unterricht und Selbststudium, 15. Aufl., Ferd. Dümmlers Verlag, Bonn 1987
Westphal, Wilhelm H.: Physik, 25./26. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1970
Gerthsen, Christian / Kneser, Hans Otto / Vogel, Helmut: Physik, 14. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1982
Tipler, Paul A. / Mosca, Gene: Physik für Wissenschaftler und Ingenieure, 6. Aufl., Spektrum Akademischer Verlag, Heidelberg 2009
Dobson, Ken / Grace, David / Lovett, David: Physics, Published by HarperCollinsPublishers Limited, London 2002
Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969
Schreiner, Josef: Lehrbuch der Physik 2. Teil, 1. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1964