| Aus Gründen der besseren Lesbarkeit wird im Folgenden die Sprachform des generischen Maskulinums
verwendet. Es wird an dieser Stelle darauf hingewiesen, dass die ausschließliche Verwendung der männlichen Form geschlechtsunabhängig
verstanden werden soll. |
Wir betrachten im Folgenden explizite Differentialgleichungen erster Ordnung, d.h. Differentialgleichungen
der Gestalt

mit gegebener Anfangsbedingung

Für viele dieser Gleichungen gibt es - oft sehr aufwendige - analytische Methoden zur Lösung,
für eine ganze Reihe von Differentialgleichungen gibt es jedoch überhaupt keine geschlossen darstellbaren analytischen Lösungen. In
solchen Fällen ist nur eine numerische Lösung möglich.
Das Ziel numerischer Verfahren ist es, ausgehend vom Punkt ( x0 , y0 ) mit Hilfe des durch
f ( x , y ) gegebenen Richtungsfeldes - f ( x , y ) ordnet jedem Punkt der xy-Ebene eine Steigung zu
- durch Iteration mit Schrittweite h > 0 eine Folge von Punkten ( xk , yk ) mit
k ≥ 0 zu berechnen, die der gesuchten Funktion y ( x ) möglichst nahe kommen.


Richtungsfeld der Differentialgleichung y' = x2 + y
(Quelle: https://homepages.bluffton.edu/~nesterd/apps/slopefields.html, 05.04.2020)
Das Euler-Verfahren
Die älteste Näherungsmethode zur numerischen Behandlung von Differentialgleichungen stammt vom
schweizer Mathematiker Leonhard Euler.

Leonhard Euler (1701 – 1783)
(Quelle: https://gonitsora.com/genesis-topology/, 02.04.2020)
Die Idee dieses Verfahrens ist in der folgenden Abbildung dargestellt.

Die exakte Lösung y ( x ) wird durch ihre Tangente im
Anfangspunkt ( x0 , y0 ) angenähert. Es gilt dann
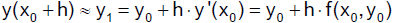
Im so erhaltenen Punkt

wenden wir dieses Verfahren erneut an. Dadurch erhalten wir eine Folge von Punkten. Es gilt für
k ≥ 0

Das Euler-Verfahren liefert nur für sehr kleine Schrittweiten h brauchbare Resultate. Betrachten
wir dazu ein Beispiel. Gegeben ist das Anfangswertproblem

mit der exakten Lösung
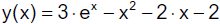
Für das Euler-Verfahren wählen wir als Schrittweite h = 0.1 und erhalten für
k ≥ 0

In der folgenden Tabelle sind die errechneten und zum Vergleich die exakten Werte angegeben.

Wir sehen, dass das Euler-Verfahren nach wenigen Iterationsschritten schon sehr stark von den exakten Werten
abweicht. Auch in der graphischen Darstellung ist diese Abweichung ersichtlich.

Die Runge-Kutta-Verfahren
Runge-Kutta-Verfahren, benannt nach den beiden deutschen Mathematikern
Carl David Tolmé Runge und Martin Wilhelm Kutta, sind die populärsten Methoden zur numerischen Lösung von
Anfangswertproblemen, da sie bei akzeptablem Rechenaufwand Resultate von hoher Genauigkeit liefern.
 |
 |
Carl David Tolmé Runge (1856 – 1927)
(Quelle: http://www.fanphobia.net/profiles/carl-david-tolme-runge/
carl-david-tolme-runge-hd-wallpaper-pic/, 20.03.2020) |
Martin Wilhelm Kutta (1867 – 1944)
(Quelle: https://www.bookofproofs.org/history/martin-wilhelm-kutta/, 20.03.2020) |
Runge-Kutta-Verfahren sind durch drei Prinzipien charakterisiert.
| • |
Sie leiten sich aus einer Taylorreihe der gesuchten
Lösungsfunktion y ( x ) ab, die nach einem Term abgebrochen wird. |
 |
 |
| • |
Sie sind sogenannte Einschritt-Verfahren, d.h. zur Berechnung von Näherungswerten an der
Stelle xk + h genügt die Information über die vorhergehende Stelle xk. |
 |
 |
| • |
Zur Berechnung der Näherungswerte wird nur die gegebene
Funktion f ( x , y ) benötigt. |
Wir betrachten die Potenzreihenentwicklung (Taylorreihe) der unbekannten
Funktion y ( x ) im Punkt ( x0 , y0 )
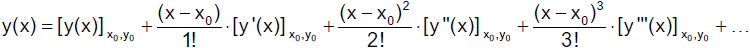
bzw.

wobei R das Lagrange'sche Restglied ist. Wir setzen x = x0 + h und
erhalten

Runge-Kutta-Verfahren bestehen nun darin, einen Näherungswert y1 für den
unbekannten Wert y ( x0 + h ) aus dieser Reihe zu berechnen, indem die Reihe nach dem m-ten Glied
abgebrochen wird. Wir bezeichnen dann m als die Ordnung des Verfahrens.

Für m = 1 erhalten wir

Das Euler-Verfahren ist daher ein Runge-Kutta-Verfahren erster Ordnung.
Im Folgenden wollen wir den Ansatz für ein Runge-Kutta-Verfahren m-ter Ordnung herleiten.
Ausgangspunkt ist die Quadraturformel

Wir substituieren
und erhalten

Wir approximieren das Integral auf der rechten Seite durch die Quadraturformel
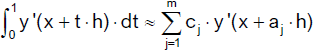
Dabei sind aj bestimmte Knoten und cj entsprechende Gewichte. Damit zumindest
y' ≡ 1 exakt integriert wird, fordern wir

Daraus folgt

Die Werte

sind unbekannt. Daher nähern wir wieder mit einer Quadraturformel, jedoch mit den alten
Knoten aj (j = 1, ..., m), da sich sonst neue Unbekannte ergeben würden.

Wieder soll y' ≡ 1 exakt integriert werden, und wir erhalten

Damit ergibt sich

Zur Abkürzung setzen wir

und erhalten

Damit ergibt sich für ein Runge-Kutta-Verfahren m-ter Ordnung der folgende Ansatz

mit den beiden Konsistenzbedingungen
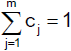
und

Die Koeffizienten aj, bj,i und cj werden in einem
sogenannten Butcher-Tableau angeordnet, benannt nach dem neuseeländischen Mathematiker John Charles Butcher.

John Charles Butcher (*1933)
(Quelle: https://inspem.upm.edu.my/laboratori/laboratory_of_computational_
sciences_and_mathematical_physics/visiting_scientists-1218, 03.05.2020) |
 |
Im Allgemeinen ist zur Bestimmung der
Funktionen fj (j = 1, ... , m) bei jedem Iterationsschritt ein Gleichungssystem zu lösen. Wir
nennen ein solches Verfahren ein implizites Runge-Kutta-Verfahren m-ter Ordnung. Bilden die Koeffizienten bj,i jedoch eine
echte untere Dreiecksmatrix, so erhalten wir ein explizites Verfahren.

Die Funktionen fj (j = 1, ..., m) können dann stufenweise
berechnet werden. Wir erhalten das folgende Verfahren

mit den Konsistenzbedingungen

und

Wir wollen nun als Beispiel explizite Runge-Kutta-Formeln zweiter Ordnung herleiten. Das
Butcher-Tableau ist gegeben durch

Damit ergibt sich der folgenden Stufen-Ansatz

mit den Konsistenzbedingungen
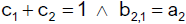
Durch Einsetzen erhalten wir

Die Konstanten a2, b2,1, c1 und c2 sind
so zu bestimmen, dass dieser Term (näherungsweise) mit der Taylorreihe

übereinstimmt. Wir entwickeln

an der Stelle h = 0 nach Potenzen von h und brechen diese Entwicklung nach dem linearen Term
ab. Wir erhalten

Durch Einsetzen ergibt sich

Wir führen jetzt für die beiden Darstellungen von y1

einen Koeffizientenvergleich durch und erhalten so das Gleichungssystem

Dieses Gleichungssystem ist unterbestimmt, es gibt daher unendlich viele Runge-Kutta-Formeln zweiter Ordnung.
Wir betrachten zwei Fälle.
Das Heun-Verfahren

Karl Heun (1859 – 1929)
(Quelle: https://en.wikipedia.org/wiki/Karl_Heun, 03.04.2020)
Wir wählen c1 = ½. Dann ist
c2 = ½, a2 = 1 und b2,1 = 1. Das Butcher-Tableau ist dann gegeben
durch

und wir erhalten für k ≥ 0

bzw.

Als geometrische Interpretation wird hier die Steigung im Euler-Verfahren durch den Mittelwert der Steigungen
an den Stellen xk und xk + h ersetzt.
Das Mittelpunkt-Verfahren
Hier wählen wir c2 = 1, woraus c1 = 0 und
a2 = b2,1 = ½ folgt. Damit erhalten wir das folgende Tableau

und für k ≥ 0
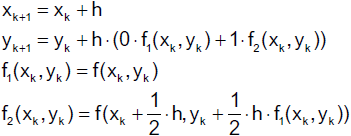
bzw.
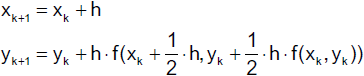
Hier entspricht die Steigung im Euler-Verfahren dem Anstieg im Mittelpunkt des
Intervalls ( xk , xk + h ).
Wir wenden das Heun-Verfahren und das Mittelpunkt-Verfahren auf das obige Beispiel an. Wir erhalten für
das Heun-Verfahren

bzw. für das Mittelpunkt-Verfahren

Die folgende Tabelle zeigt die so berechneten Werte. Zum Vergleich sind wieder die exakten Werte der
Lösungsfunktion angegeben.

War der Fehler mit dem Euler-Verfahren in diesem Beispiel noch ca. 10%, so ist er jetzt nur mehr ca. 0,4%.
Dass die Werte mittels Heun-Verfahren etwas genauer sind, liegt am gewählten Beispiel und nicht am Verfahren selbst. Bei einer anderen
Problemstellung kann es andersherum sein.
Das klassische Runge-Kutta-Verfahren vierter Ordnung
Dieses Verfahren besitzt das folgende Tableau.

Damit erhalten wir die folgenden Formeln für k ≥ 0

Die folgende Tabelle zeigt die für das obige Beispiel errechneten Werte, wobei zum Vergleich wieder die
exakten Werte angegeben sind.

Der Fehler beträgt hier nur ca. 0.00017%. Selbst nach 500 Iterationsschritten liegt er erst bei
0.0037%.
Das klassische Runge-Kutta-Verfahren vierter Ordnung lässt sich auch leicht auf Systeme von
Differentialgleichungen übertragen.
Gegeben sei das System

mit der Anfangsbedingung

dann gilt für k ≥ 0

Literatur:
Szidarovszky, Ferenc / Yankwitz, Sidney: Principles and Procedures of Numerical Analysis, 1. Aufl., Plenum Press, New York 1978
Butcher, John Charles: Numerical Methods for Ordinary Differential Equations, 2. Aufl., John Wiley & Sons Ltd, Chichester, West Sussex 2008
Hoheisel, Guido: Gewöhnliche Differentialgleichungen, 7. Aufl., Walter de Gruyter & Co, Berlin 1965