Aus Gründen der besseren Lesbarkeit wird im Folgenden die Sprachform des generischen Maskulinums verwendet. Es wird an dieser Stelle darauf hingewiesen, dass die ausschließliche Verwendung der männlichen Form geschlechtsunabhängig verstanden werden soll.

Begriffliches

Eine Epidemie (altgriechisch ἐπί "auf, bei, dazu", δῆμος "Volk") ist das vermehrte Auftreten von Krankheitsfällen mit der gleichen Ursache innerhalb einer Bevölkerung, solange diese zeitlich und örtlich begrenzt bleiben.
Ist die Ausbreitung länder- und (oder) kontinentübergreifend, so wird dies als Pandemie (altgriechisch πανδημία "das ganze Volk") bezeichnet. Im Unterschied zur Epidemie ist eine Pandemie also örtlich nicht beschränkt.

Influenza-A-Virus H1N1 - der Erreger der Spanischen Grippe 1918 – 1919
(Quelle: https://www.lemonde.fr/sante/article/2012/06/26/la-grippe-h1n1-aurait-fait-15-fois-plus-de-morts-qu-annonce_1724460_1651302.html, 28.3.2020)

Ausbreitung der Spanischen Grippe 1918 – 1919
(Quelle: https://www.researchgate.net/figure/The-path-of-the-Spanish-Flu-of-that-circled-the-world-1918-19-From-Nicholson-K-G_fig2_267376224, 27.3.2020)

Die Ausbreitung von Infektionskrankheiten

In der mathematischen Biologie wird die Ausbreitung von Infektionskrankheiten mit Hilfe von Modellen untersucht. Wie genau ein Modell die Krankheitsausbreitung in einer Population beschreibt, hängt davon ab, welche Annahmen gemacht werden. Bei der Anpassung der Modelle an einzelne Krankheiten (im Allgemeinen durch die Anpassung von Parametern) ergibt sich oft das Problem, dass es nur wenige verlässliche Daten gibt. Es ist schwierig, festzustellen, wie viele Individuen pro Zeiteinheit infiziert werden, beispielsweise weil Symptome erst nach einigen Tagen oder gar nicht auftreten. Ebenso ist es nicht leicht, die Anzahl der zu einem bestimmten Zeitpunkt infizierten Individuen zu ermitteln. Oft fehlen Anfangsbedingungen, also zum Beispiel wie viele Individuen die Krankheit in eine Population eingebracht haben und ob es bereits Individuen gibt, die gegen diese Krankheit immun sind.
Auf dem Gebiet der Modellierung von Epidemien haben sich insbesondere die beiden Schotten Anderson Gray McKendrick und William Ogilvy Kermack hervorgetan, die 1927 einige Modelle vorstellten.

Anderson Gray McKendrick (1876 – 1943) (Quelle: http://mathshistory.st-andrews.ac.uk/PictDisplay/McKendrick.html, 31.3.2020)	William Ogilvy Kermack (1898 – 1970) (Quelle: https://www.abdn.ac.uk/alumni/blog/fellows-of-the-royal-society-from-the-university/, 31.3.2020)

Die ursprüngliche Idee von Kermack und McKendrick war die Unterteilung der Population in Klassen.

	Susceptible	gesunde Individuen, die die Krankheit bekommen können
	Infected	infizierte Individuen, welche die Krankheit weitergeben können
	Removed	Individuen, die aus dem Krankheitsgeschehen ausgeschieden sind (immun, in Quarantäne, ...)

Es gibt noch weitere Verfeinerungen, die jedoch hier nicht betrachtet werden. Im Folgenden werden diese drei Klassen in graphischen Darstellungen farblich gekennzeichnet.

Wichtig ist zu erwähnen, dass die Klasseneinteilung disjunkt ist, d.h. ein Individuum der Population kann zu einem bestimmten Zeitpunkt t nur einer Klasse angehören.

Das SI - Modell

Es ist dies das einfachste Modell. Es werden nur die beiden Klassen S und I unterschieden. S(t) bezeichnet den Anteil (relative Häufigkeit) der gesunden, I(t) den Anteil der infizierten Individuen der Population zum Zeitpunkt t ≥ 0.

Wir treffen die folgenden Annahmen.

•	Jedes Individuum der Klasse S kann infiziert werden.
•	Die Zahl der Individuen in der Population ist konstant.
•	Infizierte sind sofort ansteckend.
•	Jede Gruppe interagiert miteinander mit derselben Wahrscheinlichkeit.
•	Es gibt kein Heilmittel, d.h. Infizierte werden nicht wieder gesund.
•	Gesunde werden mit der konstanten Infektionsrate a > 0 infiziert.
•	Alle Parameter bleiben im biologisch sinnvollen Bereich.

Die Krankheit verläuft so

Zur Beschreibung des zeitlichen Verlaufs der relativen Häufigkeiten S(t) und I(t) betrachten wir die beiden Funktionen

Entsprechend unseren Annahmen gelten die folgenden Bedingungen.

Außerdem sei

Die Wahrscheinlichkeit, dass ein gesundes und ein infiziertes Individuum zum Zeitpunkt t aufeinandertreffen ist wegen

durch

gegeben. Wir nehmen nun an, dass die Häufigkeit von Infektionen zum Zeitpunkt t proportional dieser Wahrscheinlichkeit ist und somit gegeben ist durch

mit

Diese Häufigkeit von Infektionen entspricht einer (momentanen) Änderungsrate von S(t) und I(t). S(t) nimmt in diesem Maße ab, I(t) im gleichen Maß zu, sodass wir das folgende System von gekoppelten Differentialgleichungen erhalten.

Zur Lösung dieses Systems betrachten wir zunächst die Gleichung

Wegen

können wir substituieren und erhalten

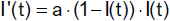
Dies ist eine logistische Differentialgleichung oder Differentialgleichung des beschränkten exponentiellen Wachstums. Sie kann durch Trennung der Veränderlichen gelöst werden.

Wir integrieren zunächst die linke Seite.

Wir substituieren

und erhalten

Insgesamt erhalten wir als Lösung

Wir stellen I(t) explizit dar.

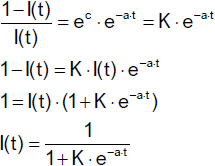
Dabei ist K eine Konstante. Zu ihrer Bestimmung setzen wir t = 0 und erhalten

Somit ergibt sich als Lösung der Differentialgleichung mit der gegebenen Anfangsbedingung

Wegen

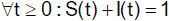
erhalten wir für S(t)

Aus

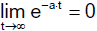
folgt

d.h. in diesem Modell erkrankt früher oder später jedes Individuum der Population unabhängig von der Infektionsrate a oder dem Anteil der zu Beginn infizierten Individuen.

Wir wollen noch eine Eigenschaft der logistischen Funktion I(t) zeigen. Für die Wendestelle t_w gilt

Wir bilden dazu die zweite Ableitung.

Wegen

ist

sodass

woraus die Aussage folgt.

Die folgende Abbildung zeigt einen für die beiden logistischen Funktionen S(t) und I(t) typischen Verlauf.

Die beiden folgenden Animationen zeigen den Einfluss der beiden Parameter I(0) und a auf den Verlauf der Funktionen S(t) und I(t).

Das SIS - Modell

Dieses Modell ist eine Modifikation des SI - Modells. Es werden wieder nur die beiden Klassen S und I betrachtet, es gelten jetzt jedoch die folgenden Annahmen.

•	Jedes Individuum der Klasse S kann infiziert werden.
•	Die Zahl der Individuen ist konstant.
•	Infizierte sind sofort ansteckend.
•	Jede Gruppe interagiert miteinander mit derselben Wahrscheinlichkeit.
•	Gesunde werden mit der konstanten Rate a > 0 infiziert.
•	Infizierte werden mit der konstanten Rate r > 0 gesund und können sich sofort wieder anstecken.
•	Alle Parameter bleiben im biologisch sinnvollen Bereich.

Die Krankheit verläuft also so.

Wir betrachten wieder die beiden Funktionen

für die die gleichen Bedingungen wie im SI - Modell gelten, also

Außerdem sei

Die Änderungsraten von S(t) und I(t) sind jetzt durch das folgende System von gekoppelten Differentialgleichungen gegeben.

mit

und

Hier ist wie im SI-Modell durch

die Häufigkeit von Infektionen zur Zeit t gegeben, während

die Häufigkeit von Gesundungen darstellt. Die Änderungsrate von S(t) setzt sich demnach aus einer Abnahme durch Neuinfektionen und einer Zunahme durch Gesundung, die von I(t) aus einer Zunahme durch Neuinfektionen und einer Abnahme durch Gesundung zusammen.

Betrachten wir die Differentialgleichung

und beachten, dass

Wir erhalten durch Substitution

Diese Gleichung ist wieder eine logistische Differentialgleichung und kann durch Trennung der Veränderlichen gelöst werden.

Wir unterscheiden hier zwei Fälle.

1. Fall: a ≠ r

Wir zerlegen den Integranden auf der linken Seite in Teilbrüche (Partialbruchzerlegung) durch den folgenden Ansatz, wobei wir aus Gründen vereinfachter Schreibweise I(t) durch x ersetzen.

Nach Multiplikation mit dem Hauptnenner erhalten wir

Um die beiden Konstanten A und B zu bestimmen setzen wir x = 0 bzw. x = 1 und erhalten das folgende Gleichungssystem

mit der Lösung

Wir erhalten

Damit ergibt sich für die Lösung der Differentialgleichung

Als explizite Darstellung für I(t) erhalten wir

wobei K eine Konstante ist. Zur Bestimmung von K setzen wir t = 0.

Durch Einsetzen erhalten wir eine Darstellung von I(t) mit gegebener Anfangsbedingung

Wegen

erhalten wir für S(t)

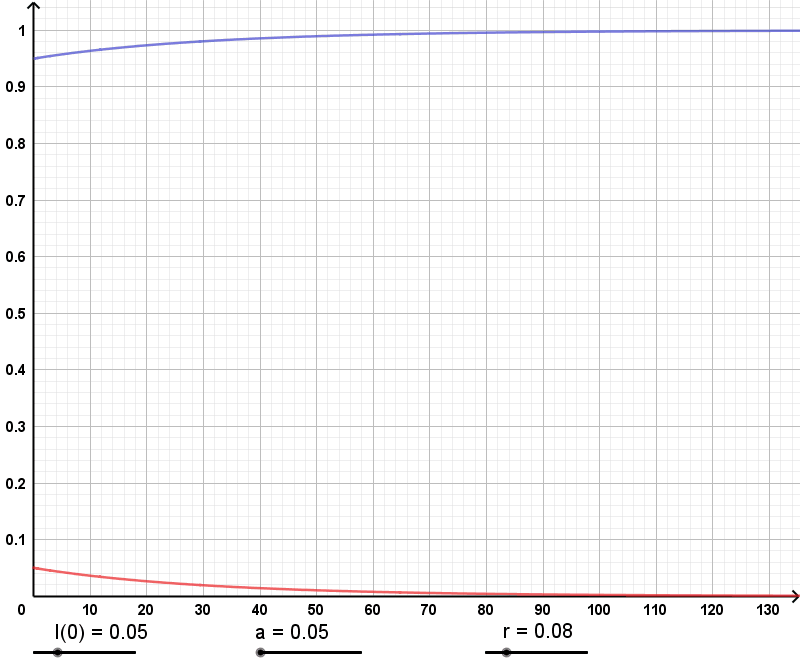
Ist a < r, also a − r < 0, so gilt

bzw.

Die Krankheit verschwindet dann vollständig aus der Population.

Für a > r erhalten wir wegen

einen unbestimmten Ausdruck, sodass wir die Regel von Regel von de l'Hospital anwenden können.

Daraus folgt

Wegen

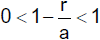
bleibt die Krankheit in der Population existent, sie erfasst aber auch nie alle Individuen gleichzeitig.

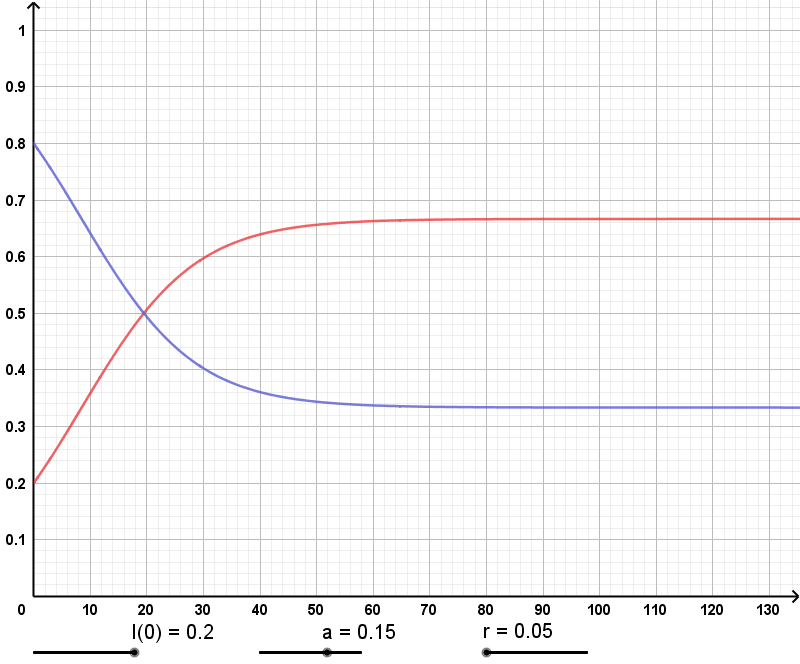
2. Fall: a = r

Hier reduziert sich die Differentialgleichung auf

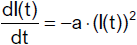
mit der folgenden Lösung

Zur Bestimmung der Konstanten K setzen wir wieder t = 0 und erhalten

Damit ist die explizite Darstellung von I(t) gegeben durch

Wegen

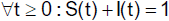
erhalten wir für S(t)

Hier gilt

d.h. die Krankheit stirbt aus.

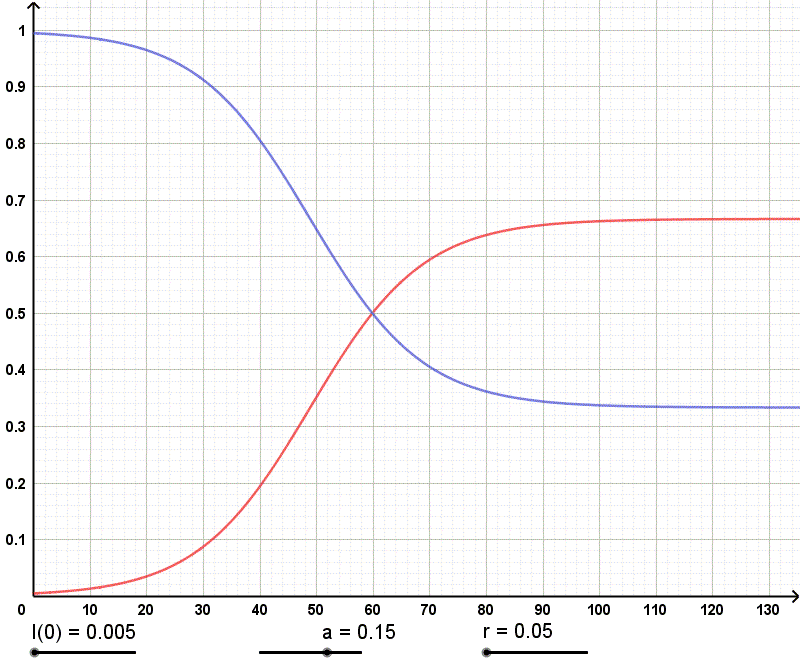
Die folgenden Animationen zeigen die Abhängigkeit von S(t) bzw. I(t) von den Parametern I(0), a und r in diesem Modell.

Das SIR - Modell

Beim SIR - Modell werden drei Klassen von Individuen betrachtet: S, I und R. Zum Zeitpunkt t ≥ 0 bezeichnet S(t) den Anteil der gesunden und infizierbaren Individuen, I(t) den Anteil der infizierten Individuen und R(t) den Anteil der aus dem Krankheitsgeschehen ausgeschiedenen Individuen (durch erworbene Immunität nach überstandener Krankheit oder Tod) der Population. Das ist das klassische Kermack-McKendrick-Modell aus dem Jahr 1927.

Das Modell kann für Krankheiten mit den folgenden Eigenschaften verwendet werden:

•	Jedes Individuum der Klasse S kann infiziert werden.
•	Jedes Individuum kann an der Krankheit nur einmal erkranken und wird danach entweder immun oder stirbt.
•	Die Zahl der Individuen ist konstant (Todesfälle werden zur Klasse R gezählt, Geburten nicht berücksichtigt).
•	Infizierte sind sofort ansteckend.
•	Jede Gruppe interagiert miteinander mit derselben Wahrscheinlichkeit.
•	Gesunde werden mit der konstanten Rate a > 0 infiziert.
•	Infizierte gehen mit der konstanten Rate r > 0 in die Klasse R über.
•	Alle Parameter bleiben im biologisch sinnvollen Bereich.

Die Krankheit verläuft also jetzt so:

Wir betrachten jetzt drei Funktionen

mit den Bedingungen

Außerdem sei

und

Die Änderungsraten von S(t), I(t) und R(t) sind jetzt durch das folgende System von gekoppelten Differentialgleichungen gegeben.

mit

und

Wie im SIS-Modell ist durch

die Häufigkeit von Infektionen zur Zeit t gegeben, während

die Häufigkeit von Gesundungen darstellt. Im Unterschied zum SIS-Modell gehen die gesund gewordenen Infizierten jedoch nicht in die Klasse S, sondern in die Klasse R über.
Das Differentialgleichungssystem ist analytisch nicht mehr einfach zu lösen, sodass wir hier eine numerische Lösung zeigen.

Die einfachste Möglichkeit ist das Euler-Verfahren. Mit Anfangsbedingung t = 0, S(0), I(0) und R(0) und geeigneter Schrittweite h > 0 ist das iterative System gegeben durch

Wir wenden jedoch das klassische Runge-Kutta-Verfahren vierter Ordnung an. Dazu bilden wir die folgenden Werte.

und erhalten

Die folgende Abbildung zeigt einen typischen Verlauf der Funktionen S(t), I(t) und R(t) nach einer Auswertung in einer Tabellenkalkulation.

Die folgende Animation zeigt die zeitliche Entwicklung dieser Epidemie.

Ist die Infektionsrate a groß, so erkranken in kurzer Zeit sehr viele Individuen.

Bei kleiner Infektionsrate erkranken weniger, die Krankheit verweilt allerdings auch länger in der Population.

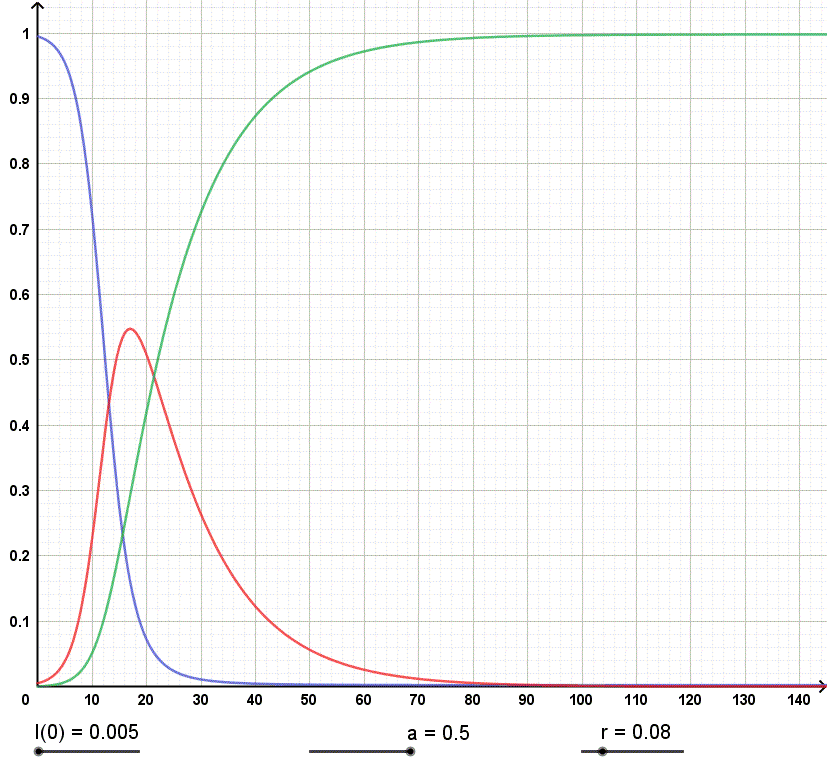
Wie sich eine Senkung der Infektionsrate um 80% auf den Verlauf der Epidemie und den Anteil der insgesamt Erkrankten in der Population auswirkt, sehen wir anhand der folgenden Animation.

Wir wollen uns nun einigen Fragen zuwenden und sie mit Hilfe des Modells analytisch beantworten.

1. Unter welchen Bedingungen kommt es zu einer Epidemie, d.h. zu einem Ansteigen von Krankheitsfällen?

Wegen

und

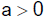
folgt aus der Gleichung

für die Funktion S(t)

d.h. die Funktion S(t) ist monoton fallend.

Es kommt zu keinem Zeitpunkt zu einem Ansteigen von Krankheitsfällen, wenn

gilt. Nun folgt aus der Gleichung

die Beziehung

Das ist aber wegen der Monotonie von S(t) genau dann erfüllt, wenn gilt

Eine Epidemie tritt genau dann auf, wenn

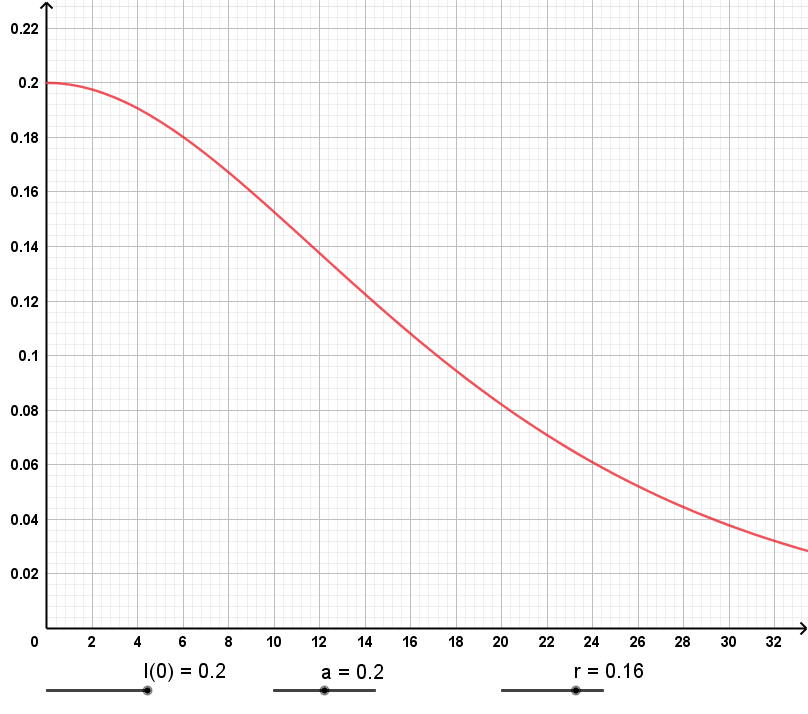
In der folgenden Animation gilt S(0)  = 0.8 und r = 0.16. Die Grenze für das Auftreten einer Epidemie liegt also bei a = 0.2.

2. Wann erreicht der Anteil der infizierten Individuen ein Maximum und wie groß ist dieses?

Aus der Gleichung

folgt

d.h.

die Funktion I(t) besitzt ein Maximum für jenes t, wo

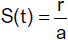
gilt. Aus den Gleichungen

bzw.

folgt

Integration ergibt

bzw.

Die Konstante c bestimmen wir für t = 0 und erhalten

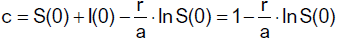
Insgesamt erhalten wir

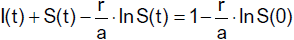
bzw.

Das Maximum von I(t) ergibt sich für

mit

In der folgenden Abbildung ergibt sich für die gegebenen Werte bei t ≈ 44.64 der Wert I_max = 0.0965.

3. Gibt es Individuen in der Population, die nicht erkranken?

Aus den Gleichungen

bzw.

folgt

Wir lösen diese Gleichung durch Trennen der Veränderlichen.

Die Konstante K ergibt sich für t = 0.

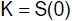
Damit erhalten wir

Wegen

gilt

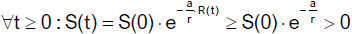
d.h. S(t) besitzt eine positive untere Schranke. Da S(t) monoton fallend und nach unten beschränkt ist, existiert der Grenzwert für t → ∞ und es gilt

bzw.

Aus der Gleichung

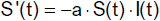
folgt

und damit

Die Krankheit verschwindet also aus der Population nicht aus Mangel an infizierbaren, sondern aus Mangel an infizierten Individuen.

Wegen

gilt

Aus Gründen der besseren Lesbarkeit setzen wir

und erhalten

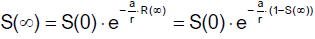
S(∞) ist also eine Lösung der transzendenten Gleichung

Für die Werte in der folgenden Abbildung S(0) = 0.995, a = 0.25 und r = 0.15 ergeben sich als Lösungen S(∞) = 0.32075 bzw. S(∞) = 1.00748, wobei letztere als biologisch nicht sinnvoll ausscheidet.

4. Wie gut passt das Modell in der Realität?

Am 4. März 1978 berichtete das britische medizinische Journal The Lancet über eine Influenzaepidemie in einer englischen Schule (boys' boarding school), die von 763 Schülern besucht wurde. Ausgelöst wurde die Epidemie durch einen Schüler, worauf insgesamt 512 Schüler erkrankten. Die Epidemie dauerte vom 22. Jänner bis zum 4. Februar 1978. Die folgende Abbildung zeigt die tatsächlichen Epidemiedaten als Punkte und die durch Anpassung der entsprechenden Parameter erzeugten theoretische Kurven.

(Quelle: Murray, James D.: Mathematical Biology I. An Introduction, 3. Aufl., Springer-Verlag, New York 2002, S. 326)

Literatur:
Hadeler, Karl Peter: Mathematik für Biologen, 1. Aufl., Springer-Verlag, Berlin Heidelberg 1974
Nöbauer, Wilfried / Timischl, Werner: Mathematische Modelle in der Biologie, 1. Aufl., Friedr. Vieweg & Sohn, Braunschweig/Wiesbaden 1979
Murray, James D.: Mathematical Biology I. An Introduction, 3. Aufl., Springer-Verlag, New York 2002