| Aus Gründen der besseren Lesbarkeit wird im Folgenden die Sprachform des generischen Maskulinums
verwendet. Es wird an dieser Stelle darauf hingewiesen, dass die ausschließliche Verwendung der männlichen Form geschlechtsunabhängig
verstanden werden soll. |

Kugelstoßpendel (Newtonpendel)
(Quelle: "Kugelstoßpendel" by gedankenstuecke is licensed under CC BY-SA 2.0,
https://search.creativecommons.org/photos/187db8c8-7eb9-4185-819b-a1164d40104b, 19.05.2021)
Im Folgenden werden Vektoren mit kursiven Fettbuchstaben dargestellt. Der Betrag eines Vektors
wird (sofern nicht anders angegeben) mit demselben Buchstaben in nicht kursiver Normalschrift
bezeichnet, z.B. |a| = a.
1. Aufgabe und Methode der Physik

Galileo Galilei (1564 – 1642)
(Quelle: https://commons.wikimedia.org/wiki/File:Galileo_Galilei_(1564-1642).
_Oil_painting_after_Justus_Wellcome_L0021979.jpg,07.05.2021) |
"Alles messen, was messbar ist, und versuchen, messbar zu machen, was es noch
nicht ist." |
|
Dieses Galileo Galilei zugeschriebene Zitat, für das es in seinen Schriften jedoch keinen Hinweis gibt,
begründet gewissermaßen die Methode physikalischen Forschens mit dem Ziel der Gewinnung von Erkenntnissen in bestimmten Bereichen der
Natur (griech. φύσις, physis). Physik ist eine Erfahrungswissenschaft, sie beruht auf Beobachtungen und
Versuchen.

Die aufgrund der Beobachtung eines
Naturphänomens (altgriech. φαινόμενον fainómenon - ein Erscheinendes) gebildete
Hypothese (altgriech. ὑπόθεσις hypóthesis - Unterstellung) für die möglichen
Ursachen dieser Naturerscheinung oder die ihr zugrunde liegenden Gesetzmäßigkeiten muss anhand ihrer Folgerungen (Voraussagen) im
Experiment überprüfbar sein und auch an dieser Überprüfung scheitern können.
Galilei schreibt dazu in treffender Weise in seinem 1623 veröffentlichten Buch "Il Saggiatore", das als ein Pionierwerk der
wissenschaftlichen Methode gilt, gegen seinen Widersacher, den Jesuitenpater Orazio Grassi:

Titelseite von Il Saggiatore,
Kupferstich von Francesco Villamena, 1623
(Quelle: https://commons.wikimedia.org/wiki/
File:Assayertitle.png, 09.05.2021) |
"Wenn Herr Grassi will, dass ich dem Suidas glaube, die Babylonier hätten
ihre Eier gekocht, indem sie sie schnell in einer Schleuder schwenkten, so will ich es glauben. Aber ich muss hinzufügen, dass die Ursache
für dieses Hartkochen eine ganz andere ist. Dazu habe ich folgende Überlegung angestellt:
Wenn es uns nicht gelingt, die gleiche Wirkung zu erzielen, die andere vor uns erreicht haben, so muss das daran liegen, dass dem Experiment ein
Element fehlt, das unseren Vorgängern zum Erfolg verhalf. Und wenn nur ein einziges Element fehlt, dann müssen wir daraus schließen,
dass dies allein die wirkliche Ursache ist.
Da uns nun weder Eier noch Schleudern noch kräftige Männer fehlen, die diese schwenken, da andererseits die Eier nicht auf diese Weise zum
Kochen gebracht werden können, sondern vielmehr, wenn sie heiß wären, schnellstens abkühlen würden - da uns also nichts
fehlt, als die Eigenschaft Babylonier zu sein, so muss diese letztere und nicht die Reibung mit der Luft die wahre Ursache für das Hartwerden der
Eier sein." |
|
Es gibt für physikalische Gesetze, Modelle und Theorien keinen endgültigen Beweis ihrer Richtigkeit
im mathematischen Sinn. Sie haben nur solange Gültigkeit, als kein Experiment oder Naturereignis ihnen widerspricht. Dies gilt für viele
Aussagen.
Betrachten wir dazu die Aussage: "Alle Raben sind schwarz." Diese Aussage ist ein Schluss von bisherigen Beobachtungen, d.h. vom Besonderen
auf das Allgemeine. Streng genommen ist es jedoch unmöglich, von empirischen Sätzen zu allgemeingültigen Aussagen zu gelangen. Aus
besonderen Urteilen lassen sich allgemeine nur ableiten, wenn alle Einzelfälle gegeben sind (vollständige Induktion). Sind sie nicht
gegeben (unvollständige Induktion), so ist der Schluss nur wahrscheinlich. Aber auch dazu bedarf es bestimmter hypothetischer
Voraussetzungen, z.B. Gleichförmigkeit der Natur. Wir nehmen daher an, dass das Naturgeschehen nach bestimmten Gesetzen abläuft und es kein
ungesetzmäßiges Verhalten in der Natur gibt.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/free-icon/raven_92031, 20.05.2021) |
 |
Oft wird von der Physik eine Erklärung des Naturgeschehens verlangt. Eine letzte Erklärung kann die
Physik nicht geben. So gibt es z.B. auf die Frage: "Warum fällt ein Stein lotrecht zur Erde?" die Antwort: "Weil zwischen dem Stein
und der Erde eine Gravitationskraft wirkt." Wir können diese Kraft und ihre Abhängigkeiten im Gravitationsgesetz beschreiben und somit
'verstehen'. Warum es so etwas wie Gravitation überhaupt gibt, dafür können wir keinen Grund angeben.
2. Größen und Einheiten
Physik beschäftigt sich nur mit jenen Merkmalen in der Natur, die im Prinzip gemessen werden können.
Solche Merkmale (Eigenschaften) physikalischer Objekte nennen wir physikalische Größen. Das Messen (d.h. Vergleichen) einer
physikalischen Größe G ist nur dann möglich, wenn eine geeignete Messvorschrift definiert wurde. Dazu gehören die Definition
einer Maßeinheit [G] und Vorschriften für die Feststellung von Maßgleichheit bzw. Maßvielfachheit.
Das Ergebnis einer Messung ist eine Maßzahl G*, die angibt, wie oft die Maßeinheit [G] in der zu messenden
Größe G enthalten ist. Jede physikalische Größe G ist daher das Produkt aus einer Maßzahl G* und einer
Maßeinheit [G].

Als Beispiel betrachten wir die Messung der Länge einer Strecke s.

Grundgrößen (Basisgrößen)
Grundgrößen sind durch die Angabe ihrer Messvorschrift definiert. Die zugehörigen Einheiten
heißen Grund- oder Basiseinheiten. Es gibt sieben Grundgrößen, die mit ihren Einheiten im Internationalen
Einheitensystem (SI - Système international d’unités) definiert sind. Die Auswahl der Grundgrößen erfolgte nach
praktischen Gesichtspunkten. Das SI ist ein metrisches System (d.h., eine Grundeinheit ist der Meter), es ist dezimal (d.h., die
verschiedenen Einheiten, mit denen man eine Größe angeben kann, unterscheiden sich nur um ganze Zehnerpotenzen) und es ist
kohärent (d.h., jede abgeleitete Einheit ist ein Produkt von Potenzen der Grundeinheiten ohne zusätzliche numerische Faktoren). Seit
2019 sind alle Grundeinheiten über Naturkonstanten definiert, indem für diese ein exakter Wert festgelegt wurde. Die sieben
Grundgrößen und ihre Einheiten sind:

Abgeleitete Größen
Abgeleitete Größen werden durch Definitionsgleichungen mit Hilfe der Grundgrößen
definiert. Ihre Messvorschriften sind in den Definitionsgleichungen enthalten. Als Beispiel betrachten wir den Flächeninhalt eines Rechtecks mit
den Seiten a und b.

Damit ist die Messung des Flächeninhalts eines Rechtecks auf die Längenmessung der beiden Seiten
zurückgeführt.
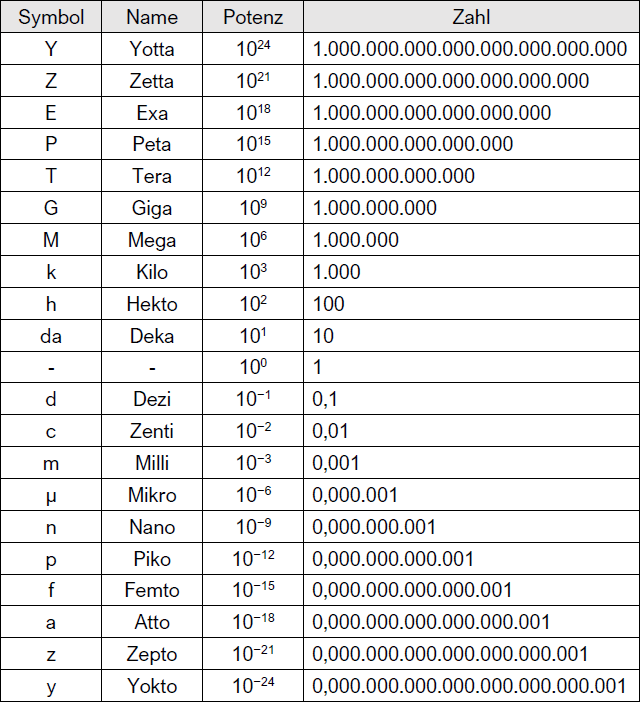
Teile und Vielfache
Jeder physikalischen Größe ist nur eine Maßeinheit zugeordnet. Da diese jedoch nicht immer
eine passende Größe hat, werden oft Teile oder Vielfache dieser Maßeinheit verwendet, zu deren Bildung die folgenden Vorsilben
verwendet werden müssen.
3. Die Grundgröße Zeit

Augustinus von Hippo (354 – 430), Lateranbasilika, 6. Jahrhundert
(Quelle: https://commons.wikimedia.org/wiki/File:AugustineLateran.jpg, 13.05.2021) |
"Was ist also die Zeit? Wenn mich niemand darüber fragt, so weiß ich es;
wenn ich es aber jemandem auf seine Frage erklären möchte, so weiß ich es nicht."
(Augustinus, Bekenntnisse (Confessiones), 397 - 401. XI, 14) |
|

Sir Isaac Newton (1642 – 1727)
(Quelle: "Sir Isaac Newton" by aldoaldoz is licensed under CC BY-NC-SA 2.0,
https://search.creativecommons.org/photos/dccf4c2a-b8b5-49f6-93d7-e084c7ade50d, 28.08.2020) |
"... die absolute, wahre und mathematische Zeit, in sich und ihrer Natur nach ohne
Beziehung zu irgendetwas Äußerem, fließt gleichmäßig dahin ..."
(Isaac Newton, Philosophiae naturalis principia mathematica, 1687) |
|
Der Begriff der Zeit hat seine Grundlage in Veränderungen. Dadurch werden Ereignisse in einer
Reihenfolge (vorher - nachher) angeordnet bzw. der "zeitliche Abstand" zweier Ereignisse bestimmt. Durch diese Abfolge von
Ereignissen hat die Zeit eine eindeutige unumkehrbare Richtung. In einer völlig unveränderlichen Welt wäre der Begriff der Zeit ohne
Sinn. Auch der Newtonsche Begriff einer sogenannten "absoluten Zeit", an dem bis zum Ende des 19. Jahrhunderts festgehalten wurde, ist
physikalisch nicht sinnvoll, da er keine experimentelle Überprüfung zulässt.
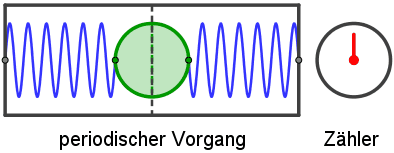
Die Zeit erscheint uns kontinuierlich und weist an sich keine Unterteilung auf. Ein Zeitmaß muss daher erst definiert werden. Alle
gebräuchlichen Zeitmesser (Uhren) bestehen im Wesentlichen aus zwei Komponenten: Die erste ist ein Vorgang, an dem sich möglichst
gleichartige Abschnitte des Geschehens feststellen lassen, der also etwa periodisch ist. Die zweite Komponente ist eine Vorrichtung, die diesen
periodischen Vorgang zählt.
 |
 |
Der periodische Vorgang kann zum Beispiel die Erdrotation sein wie bei der Sonnenuhr. Der Vorgang kann ein
schwingendes Pendel sein, dann hat man eine Pendeluhr. Wenn es gelingt, Atome irgendwie zum "Schwingen" zu bringen, dann spricht man von einer
Atomuhr.
Die "Sonnensekunde"
Das natürliche Zeitmaß für uns Menschen ist der durch die Erdrotation bedingte Tag. Der wahre
Sonnentag ist als der Zeitraum von einem Sonnenhöchststand (obere Kulmination) bis zum nächstfolgenden am gleichen Ort definiert.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/sonne_869767, 13.05.2021) |
 |
Die wahren Sonnentage dauern allerdings im Laufe eines Jahres unterschiedlich lange. Bedingt ist dies
einerseits durch die Neigung der Erdachse gegenüber ihrer Bahnebene (Schiefe der Ekliptik) und andererseits durch die Ellipsenform der
Erdbahn um die Sonne. Die längsten wahren Sonnentage fallen ungefähr auf die Sonnenwenden, die kürzesten auf die Tagundnachtgleichen,
wobei sich ein Zeitunterschied von ca. einer halben Minute ergibt.
Man führte daher den mittleren Sonnentag als Jahresmittel der wahren Sonnentage ein aufgeteilt in 24 Stunden zu je 60 Minuten zu je
60 Sekunden und gelangte zu folgender Festlegung:
Die Einheit der Zeit ist 1 Sekunde (1 s). 1 s ist 1/86400 des mittleren
Sonnentages.
Dabei ist die Zahl 86400 im Grunde willkürlich gewählt und hat eher traditionellen Hintergrund.
Eine formale Definition dieser "Sonnensekunde" als verbindliches Maß für die Zeit im Sinne des Internationalen Einheitensystems SI hat
es jedoch nie gegeben.
Vom Sonnentag ist der siderische Tag zu unterscheiden. Dieser bezieht sich auf den Fixsternhimmel als Hintergrund und beschreibt die Zeitspanne
zwischen zwei aufeinanderfolgenden oberen Kulminationen eines weit entfernten Sterns. Ein siderischer Tag dauert
ca. 23 Stunden 56 Minuten, ist also kürzer als ein Sonnentag. Bei einem Sonnentag vollführt die Erde wegen ihrer
Bewegung um die Sonne nämlich etwas mehr als eine Umdrehung um ihre Achse.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020,
Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/sonne_869767, 13.05.2021) |
 |
Da die Erdrotation durch die Gezeitenreibung allmählich abgebremst wird (vor 400 Millionen
Jahren hatte ein Jahr 400 Tage), ändert sich die Dauer eines mittleren Sonnentages fortlaufend, sodass das Internationale Komitee für
Maß und Gewicht im Jahr 1956 die SI-Sekunde als einen bestimmten Bruchteil des tropischen Jahres festgelegt hat, da die Bahnbewegung der
Erde um die Sonne stabiler als die Erdrotation ist. Das tropische Jahr ist die Zeitdauer zwischen zwei aufeinander folgenden Durchgängen der
"mittleren Sonne" durch den "mittleren Frühlingspunkt". Wegen der Veränderlichkeit des tropischen Jahres wurde der Definition dieser
sogenannten Ephemeridensekunde ein bestimmtes tropisches Jahr zugrunde gelegt, und zwar das differenzielle tropische Jahr für den
0. Januar 1900 um 12 Uhr Ephemeridenzeit.
Die "Cäsium-Sekunde"
Seit 1967 ist die SI-Sekunde wie folgt definiert:
| |
Die Einheit für die Zeit ist die Sekunde (s). Die Sekunde ist definiert, indem
für die Cäsiumfrequenz ΔνCs, der Frequenz des ungestörten Hyperfeinübergangs des Grundzustands des
Cäsiumatoms 133, der Zahlenwert 9 192 631 770 festgelegt wird, ausgedrückt in der Einheit Hz, die
gleich s−1 ist. |
|
Cäsium ist eine Reinelement, in der Natur kommt nur das Nuklid Cäsium 133 vor. Dieses Nuklid
ist das einzige nicht radioaktive des Cäsiums. Für die obige Definition der SI-Sekunde sind zwei Energiezustände des Cäsiumatoms
von Bedeutung, ein Grundzustand (Energiezustand 1) und ein angeregter
Zustand (Energiezustand 2). Durch den Einfluss elektromagnetischer Wellenstrahlung kann ein
Cäsiumatom vom Grundzustand in den angeregten Zustand übergehen. Dabei muss die Frequenz dieser elektromagnetischen Welle, die im
Mikrowellenbereich des elektromagnetischen Spektrums liegt, 9 192 631 770 Hz betragen.
Cäsiumatome in diesen beiden Zuständen besitzen magnetische Eigenschaften und können durch ein
Magnetfeld sortiert (getrennt) werden.
Die folgende Abbildung zeigt den grundsätzlichen Aufbau einer Cäsium-Atomuhr.

In einem Atomofen befinden sich zunächst zu gleichen Anteilen angeregte Cäsiumatome sowie
Cäsiumatome im Grundzustand. Auf ihrem Weg durch eine Vakuumkammer passieren die Cäsiumatome einen Sortiermagneten, der die angeregten Atome
aussortiert und nur Atome im Grundzustand durchlässt. Im Mikrowellenresonator werden die Cäsiumatome mit elektromagnetischer Strahlung
bestrahlt. Ist die Frequenz dieser Strahlung passend, werden die Atome angeregt. Anschließend sortiert ein Magnet die Atome erneut und ein
Detektor registriert, bei wie vielen Atomen sich der Energiezustand durch die Bestrahlung im Mikrowellenresonator geändert hat. Die Frequenz der
Mikrowellenstrahlung wird so lange angepasst, bis sich ein Maximum an angeregten Cäsiumatomen ergibt: In diesem Resonanzfall schwingt die
Mikrowelle 9 192 631 770 mal pro Sekunde. Nach dieser Anzahl von Schwingungen wird der Sekundenzeiger der Uhr um eine Sekunde
weitergestellt.

Atomuhr CS-2 der Physikalisch Technischen Bundesanstalt Braunschweig
(Quelle: https://commons.wikimedia.org/wiki/File:Atomuhr-CS2.jpg, 17.05.2021)
Die relative Standardabweichung typischer Cäsium-Atomuhren beträgt 10−13, d.h. der
Gangfehler beträgt 1 Sekunde in ca. 300 000 Jahren. Zum Vergleich gelten Quarzuhren mit Abweichungswerten um die
25 Sekunden pro Jahr als hochpräzise.
Da in einer Atomuhr die Frequenz einer atomaren Resonanz gemessen wird, gelingt dies umso präziser, je höher die Frequenz der Resonanz ist.
Sichtbares Licht hat eine viel höhere Frequenz als die bei Cäsium genutzte Mikrowellenstrahlung. Eine Atomuhr, die mit einer optischen
Resonanz arbeitet, kann aus diesem Grund deutlich genauer sein. So erreichen Atomuhren, die mit Strontium 87 - Atomen und einer
Frequenz von 429 228 004 229 874 Hz arbeiten, eine relative Ganggenauigkeit von 10−17, d.h. 1 Sekunde
in 3 000 000 000 Jahren. Es kann daher durchaus sein, dass die Cäsium-Sekunde eines Tages durch eine neue Definition ersetzt
wird.
Größenordnungen der Zeit

* beschreibt das kleinstmögliche Zeitintervall, für das die bekannten Gesetze der Physik gültig sind
4. Die Grundgröße Länge
Aus dem Gebrauch im Alltag verbinden wir mit dem Begriff "Länge" gewisse Vorstellungen. In der Physik
müssen wir dazu Messvorschriften angeben.
Definition der Maßgleichheit
Zwei Strecken (Maßstäbe) haben die gleiche Länge, wenn ihre Endpunkte paarweise
gleichzeitig zur Deckung gebracht werden können.
In dieser Definition ist das Wort "gleichzeitig" von besonderer Bedeutung. Es impliziert die korrekte Messung
von Längen: Die Länge einer Strecke messen heißt, Anfangspunkt A und Endpunkt E dieser Strecke gleichzeitig bestimmen.
Bestimmen wir die Koordinaten der Punkte A und E nicht gleichzeitig, so erhalten wir ein
inkorrektes Messergebnis.
Mit Albert Einsteins Spezieller Relativitätstheorie 1905 wurde klar, dass den Begriffen "gleichzeitig"
bzw. "Gleichzeitigkeit" kein absoluter, sondern ein relativer Charakter zukommt. Ereignisse, die für einen Beobachter gleichzeitig stattfinden,
sind für einen anderen Beobachter möglicherweise nicht gleichzeitig. So ist es möglich, dass zwei Beobachter bei ein und derselben
Längenmessung zu verschiedenen Messergebnissen gelangen, obwohl sie jeweils aus ihrer Sicht die Messvorschrift eingehalten haben.
Definition der Maßvielfachheit
Eine Strecke b hat die 2, 3, ..., n-fache Länge einer Strecke a, wenn sie
sich in 2, 3, ..., n gleiche Teilstrecken der Länge a unterteilen lässt.
Mit dieser Definition bleibt bei Vereinigung oder Teilung von Strecken die Summe aller
Längenmaßzahlen unverändert. Zur Vervollständigung der Messvorschrift fehlt noch die Definition einer Maßeinheit.
Der Urmeterstab
Der Urmeter war die bis 1960 gültige Maßverkörperung der Längeneinheit
Meter (griech. μέτρον métron - Maß). Bei der Einführung des metrischen Einheitensystems 1791
wurde der Meter zunächst als zehn-millionster Teil des Viertels des durch Paris verlaufenden Erdmeridians (Erdmeridianquadrant)
festgelegt, der dazu geodätisch vermessen wurde.

1889 wurde ein Metallstab aus einer Platin-Iridium-Legierung mit x-förmigem Querschnitt hergestellt, der
an beiden Enden eine Markierung mit drei Strichen (Kerben) aufweist und damit die Längeneinheit definierte.
| |
Die Einheit der Länge ist der Meter (m). Ein Meter ist der Abstand der
Mittelstriche der auf dem in Sèvres bei Paris aufbewahrten Urmeterstab angebrachten Strichgruppen bei 0° C. |
|

Kopie Nr. 18 des Urmeterstabes der Physikalisch Technischen Bundesanstalt Braunschweig;
der rechte Teil der Abbildung zeigt eine mikroskopische Aufnahme des Mittelstrichs.
(Quelle: http://www.chemie-master.de/Periodensystem/index.php?Ir#gsc.tab=0, 19.05.2021)
Diese Längendefinition besaß eine Genauigkeit von 10−7. Kopien dieses
Meterprototyps wurden an die Eichinstitute in vielen Ländern vergeben. So erhielt das damalige Kaiserreich Österreich–Ungarn unter
anderem die Kopie Nr. 19, die heute im Internationalen Büro für Maß und Gewicht (BIPM - Bureau International des Poids
et Mesures) in Sèvres aufbewahrt wird.
Obwohl bei der Herstellung der Meterprototypen größter Wert auf Genauigkeit gelegt wurde, war klar, dass es bei ihrer Anfertigung zu
Abweichungen kommen musste. Ebenso gab es das Risiko von Beschädigungen bei regelmäßigen Vergleichen der Kopien untereinander bzw. mit
dem Original.
Daher wurde der Meter 1960 neu definiert: Ein Meter war das 1 650 763,73fache der Wellenlänge der von Atomen des Nuklids
Krypton 86 beim Übergang vom Zustand 5d5 in den Zustand 2p10 ausgesandten, sich im Vakuum ausbreitenden
Strahlung. Der Zahlenwert wurde dabei so gewählt, dass das Ergebnis dem bis 1960 gültigen Meter innerhalb der damaligen Messgenauigkeit
entsprach. Die Definition des Meters beruhte damit nicht mehr auf einem Kunstmaß (Urmeterstab), sondern auf einem
Naturmaß (Naturkonstante) und ließ sich in jedem Labor mit entsprechender Ausrüstung mit einer Genauigkeit von
10−8 realisieren.
Mit der Entdeckung des Lasers wurden in den folgenden Jahren immer bessere Lichtquellen und Messmethoden entwickelt. Insbesondere ließ sich die
Lichtgeschwindigkeit auf 1 m/s genau bestimmen, sodass es 1983 zu der noch heute gültigen Definition für die Einheit der Länge
kam.
Der "Lichtmeter"
| |
Die Einheit für die Länge ist der Meter (m). Der Meter ist definiert,
indem für die Lichtgeschwindigkeit im Vakuum c der Zahlenwert 299 792 458 festgelegt wird, ausgedrückt in der
Einheit m/s, wobei die Sekunde mittels ΔνCs definiert ist. |
|
Damit ist die Längenmessung im Prinzip auf die Zeitmessung zurückgeführt. Je genauer die
Laufzeit eines Lichtsignals gemessen werden kann, desto genauer lässt sich die zugehörige Laufstrecke ermitteln. So ermittelt auch das
Global-Positioning-System die Position durch eine Zeitmessung.
Größenordnungen der Länge

* ist die kleinste Länge, in die sich der Raum aufgrund der Unschärferelation einteilen lässt.
Die Fläche
So wie die Länge die "Größe" von Linien misst, bestimmt die Fläche die
"Größe" von Figuren, d.h. von zweidimensionalen Objekten. Wir beschränken unsere Betrachtungen im Folgenden auf ein Rechteck. Wir
könnten die Größe eines Rechtecks nach verschiedenen Gesichtspunkten beurteilen: Größe des Umfangs, Länge der
Diagonalen, ... Bei der Teilung oder Vereinigung von Rechtecken würde sich dann aber die Summe der Maßzahlen ändern.

In der obigen Abbildung ist z.B. die Umfangsumme der beiden Teilrechtecke um 2b größer als der
Umfang des ungeteilten Rechtecks. Beurteilt man die Größe eines Rechtecks jedoch nach dem Produkt zweier aufeinander normaler Seiten, so
ist dies nicht der Fall.

Wir definieren daher:
Die Größe einer Figur wird durch ihre Fläche A gemessen. Unter der Fläche A
eines Rechtecks verstehen wir das Produkt der Längen a, b der aufeinander normalen Seiten:
 |
Definitionsgleichung der Fläche eines Rechtecks |
 |
 |
 |
Definition der Einheit der Fläche |
Die Einheit der Fläche ist der Quadratmeter (m2). 1 m2 ist gleich der
Fläche eines Quadrats mit 1 m Seitenlänge.
Das Volumen
Zur Festlegung von Punkten im Raum sind drei Maßzahlen (Koordinaten) notwendig. Wir sagen
daher: "Der Raum ist dreidimensional." Dreidimensionale Objekte bezeichnen wir als Körper.

Analog zur Fläche definieren wir:
Die Größe eines Körpers wird durch sein Volumen V gemessen. Unter dem Volumen eines
Quaders verstehen wir das Produkt der Längen a, b, c dreier paarweise aufeinander normaler Kanten.
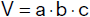 |
Definitionsgleichung des Volumens eines Quaders |
 |
 |
 |
Definition der Einheit des Volumens |
Die Einheit des Volumens ist der Kubikmeter (m3). 1 m3 ist gleich dem Volumen
eines Würfels mit 1 m Kantenlänge.
5. Grundsätzliches über Körper
Körper haben ein Volumen
Taucht man einen festen Körper in ein mit Wasser gefülltes Gefäß, so steigt der
Wasserspiegel, da der Körper eine gewisse Wassermenge verdrängt. Auf diese Weise kann auch das Volumen von sehr unregelmäßig
geformten (festen) Körpern z.B. mit Hilfe eines Messzylinders bestimmt werden.

(Quelle: Icons erstellt von Pixel perfect,
https://www.flaticon.com/de/kostenloses-icon/zylinder_1200865,
22.05.2021) |
 |

(Quelle: https://commons.wikimedia.org/wiki/File:
Graduated_Cylinder_low_form_250ml.svg, 22.05.2021) |
 |
Auch gasförmige Körper besitzen ein Volumen. Taucht man eine oben geschlossene
Glasröhre ins Wasser, so dringt das Wasser kaum ein. Der Wasserspiegel zeigt das Volumen der eingeschlossenen Luft. Mit zunehmender Eintauchtiefe
steigt der Wasserspiegel etwas an, das Volumen der Luft ist also leicht veränderlich. |
|
Körper ermöglichen die Angabe räumlicher Beziehungen
Wir stellen uns die Frage, ob der Begriff "Raum" in der Physik einen Sinn hat, wenn es keine Körper
gibt. In der Philosophie wird ein solcher Raum manchmal als "Raum an sich" oder "absoluter Raum"
bezeichnet (lat. absolvere - loslösen). Isaac Newton, der zur Begründung der Mechanik wesentliche Beiträge geleistet hat,
schreibt dazu Folgendes in seiner "Philosophiae naturalis principia mathematica".
| |
"Der absolute Raum bleibt vermöge seiner Natur und ohne Beziehung auf einen
äußeren Gegenstand stets gleich und unbeweglich. Der relative Raum ist ein Maß oder beweglicher Teil des ersteren, welcher von
unseren Sinnen durch seine Lage gegen andere Körper bezeichnet und gewöhnlich für den unbeweglichen Raum genommen wird; z.B. ein Teil
des Raumes innerhalb der Erdoberfläche, ... ein Teil des Himmels, bestimmt durch seine Lage gegenüber der Erde ..." |
|
Wir haben am Anfang den Grundsatz aufgestellt, dass wir uns in der Physik nur mit Begriffen beschäftigen
wollen, die im Prinzip einer Messung zugänglich sind. Wie soll ein "absoluter Raum", in dem es keine Gegenstände und daher auch keine
Maßstäbe gibt, gemessen werden? Der Begriff "absoluter Raum" ist daher in der Physik nicht sinnvoll. Erst die Existenz von Körpern
ermöglicht die Angabe von räumlichen Beziehungen zwischen diesen Körpern mit Hilfe eines Koordinatensystems d.h. Bezugssystems. Auch
Newton erkannte bereits, dass sich der absolute Raum nicht nachweisen lässt.
| |
"Die wahren Bewegungen der Körper zu erkennen und von den scheinbaren scharf
zu unterscheiden, ist übrigens sehr schwer, weil die Teile jenes unbeweglichen Raumes, in denen die Körper sich wahrhaft bewegen, nicht
sinnlich erkannt werden können." |
|
Trotzdem wurde der Begriff des "absoluten Raumes" in der Physik bis zum Ende des 19. Jahrhunderts
aufrechterhalten, da mit ihm ein ausgezeichnetes Bezugssystem verbunden gewesen wäre.
Die räumlichen Beziehungen zwischen Körpern können sich ändern
Körper können in Ruhe oder in Bewegung sein. Ruhe und Bewegung sind in diesem Zusammenhang jedoch
relative Begriffe und machen nur Sinn gegenüber einem gegebenen Koordinatensystem (Bezugssystem). Ein Körper ruht in einem
Bezugssystem, wenn sich seine Koordinaten bezüglich dieses Systems nicht ändern. Er ist in Bewegung, wenn sich seine Koordinaten
bezüglich dieses Systems ändern.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020,
Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021) |
 |
Im obigen Bild ist die Person bezüglich eines mit dem "Zug" verbundenen Koordinatensystems in Ruhe,
bezüglich des Systems "Bahnsteigs" jedoch in Bewegung.
Zwischen Körpern gibt es Wechselwirkungen
Betrachten wir zunächst einige Beispiele (Experimente).
Ein kleiner Magnet und ein Stück Eisen schwimmen auf Korken vorerst ruhend auf Wasser. Bei nicht zu
großer Entfernung geraten beide Körper alsbald in Bewegung und schwimmen entlang ihrer Verbindungslinie aufeinander zu (magnetische
Wechselwirkung). Bei sehr großer anfänglicher Entfernung setzt keine Bewegung ein.
Zwischen zwei mit einem Faden verbundenen Spielzeugwagen ist eine Blattfeder gespannt. Nach Durchtrennen des
Fadens kommen sie in entgegengesetzte Richtungen in Bewegung (elastische Wechselwirkung).

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021) |
 |
Lässt man eine Kugel los, so fällt sie lotrecht zu Boden (Gravitationswechselwirkung). Diese
Wechselwirkung scheint sehr einseitig zu sein, da wir von einer Bewegung der Erde nichts merken, da diese infolge der Größe der Erde
unmessbar klein ist.

(Quelle: Icon von Icons8, https://icons8.de/icons/set/kugel, 10.04.2021) |
 |
Körper können ihren Bewegungszustand gegenseitig ändern. Wir bezeichnen dies als
Wechselwirkung zwischen diesen Körpern. Die Wirkung ist nie einseitig; wenn ein Körper A auf einen Körper B einwirkt, dann
wirkt auch umgekehrt der Körper B auf den Körper A ein. Ist die Entfernung zwischen zwei Körpern sehr groß, dann wird
die Wechselwirkung zwischen ihnen unmessbar klein.
Ein von allen anderen Körpern weit genug entfernter Körper unterliegt keiner messbaren Wechselwirkung. Wir nennen einen solchen Körper
einen freien Körper. Ein freier ruhender Körper verharrt in Ruhe.
Alle Körper sind träge
Wir betrachten eine Kugel, die auf der linken Seite entlang einer schiefen Ebene herabrollt. Wenn die Kugel
keiner Wechselwirkung mit der Unterlage (Reibung) unterliegt, steigt sie rechts entlang einer zweiten schiefen Ebene wieder bis zur
Anfangshöhe empor.
Je geringer die Neigung der rechten schiefen Ebene gewählt wird, desto kleiner fällt die
Verlangsamung (Verzögerung) der aufsteigenden Kugel aus.
Geht man bei der rechten schiefen Ebene zur Waagrechten über, so muss sich die Kugel nach dem
Herabrollen gleichförmig fortbewegen.
Wir können somit das sogenannte Beharrungsgesetz (Trägheitsgesetz) formulieren.
| |
Jeder freie ruhende Körper verharrt in Ruhe. Jeder freie Körper, wenn er in
Bewegung gesetzt und sich dann selbst überlassen wird, verharrt im Zustand gleichförmiger Bewegung auf gerader Bahn. Änderung von Ruhe
und Bewegung ist nur durch Wechselwirkung mit anderen Körpern möglich. |
|
Bis ins Mittelalter war man nach der Lehre des Aristoteles der Meinung, dass ein Körper nicht von selbst
dauernd in Bewegung verharren kann, sondern dass zur Aufrechterhaltung der Bewegung eine ständige "Kraft" nötig ist. Erst Galileo Galilei
hat das Beharrungsgesetz verwendet, wenn auch noch in einer fehlerhaften Form. Isaac Newton gab dem Beharrungsgesetz erstmals eine korrekte
Formulierung und erkannte darin eines der Grundgesetze der Physik.

Newtons erstes und zweites Gesetz in der Originalausgabe
der Philosophiae naturalis principia mathematica von 1687
(Quelle: https://commons.wikimedia.org/wiki/File:
Newtons_laws_in_latin.jpg, 26.05.2021) |
"Corpus omne perseverare in statu suo quiescendi vel movendi
uniformiter in directum, nisi quatenus illud a viribus impressis cogitur statum suum mutare." |
|
Angesichts der Tatsache, dass alle auf der Erde in Bewegung gesetzten Körper "ganz von alleine" wieder
zum Stillstand kommen, bedurfte die Aufstellung des Beharrungsgesetzes eines hohen Maßes an Abstraktion.
Inertialsysteme
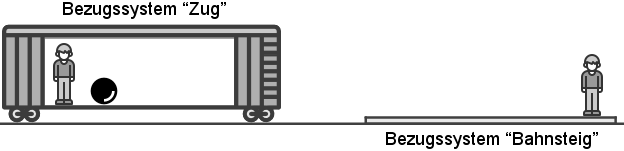
Das Trägheitsgesetz gilt nicht in beliebigen Bezugssystemen. Betrachten wir dazu das folgende
Beispiel.
(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020,
Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021,
Icon von Icons8, https://icons8.de/icons/set/kugel, 10.04.2021) |
 |
In einem Zug befindet sich eine Kugel. Solange sich der Zug gleichförmig bewegt, ist die Kugel für
einen Beobachter im Zug im Zustand der Ruhe und für einen Beobachter auf dem Bahnsteig im Zustand der gleichförmigen Bewegung. Für
beide Beobachter gilt das Trägheitsgesetz. Hält der Zug jedoch plötzlich an, so ändert die Kugel für den Beobachter im Zug
ohne erkennbare Wechselwirkung ihren Bewegungszustand. In seinem System gilt das Trägheitsgesetz nun nicht mehr. Für den Beobachter am
Bahnsteig ändert sich nichts.
Das Trägheitsgesetz gilt nur in speziellen Bezugssystemen. Solche Bezugssysteme heißen Inertialsysteme (lat. inertia -
Trägheit). Zu einem gegebenen Inertialsystem ist ein dazu verschobenes, ein dazu verdrehtes und ein dazu gleichförmig geradlinig bewegtes
Bezugssystem ebenfalls wieder ein Inertialsystem. So ist in der folgenden Animation jedes der vier durch einen Beobachter dargestellten Bezugssysteme
ein Inertialsystem. Die Kugel verharrt in allen vier Systemen im Zustand der Ruhe oder der gleichförmigen Bewegung auf gerader Bahn.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020,
Icon von Icons8, https://icons8.de/icons/set/kugel, 10.04.2021) |
 |
Ein rotierendes Bezugssystem wie das Bezugssystem "Erde" ist kein Inertialsystem. In der folgenden
Animation (Ausschnitt aus einem Video) läuft eine Kugel entlang einer Rinne auf eine rotierende Scheibe. Bewegt sich die Kugel nach
Verlassen der Rinne aus der Sicht des "Labors" gleichförmig geradlinig, so verläuft ihre Bewegung aus der Sicht einer mitrotierenden Kamera
ohne erkennbare Wechselwirkung krummlinig. Das Trägheitsgesetz gilt also für einen mitrotierenden Beobachter nicht mehr.

(Quelle: Jodl, Hans-Jörg, IWF (Göttingen), Coriolis- und Zentrifugalkraft im rotierenden Bezugssystem, https://doi.org/10.3203/IWF/C-13095,
https://av.tib.eu/media/10796, 01.09.2020) |
 |
6. Skalare und vektorielle Größen
Zur Angabe mancher Größen in der Physik genügt eine einzige Zahl. Wir nennen solche
Größen skalare Größen (Skalare) oder auch ungerichtete Größen. Dazu gehört beispielsweise die Länge,
die Zeit oder das Volumen. Andere physikalische Größen sind durch einen bestimmten Betrag (Zahl) und eine Richtung gekennzeichnet,
z.B. die geradlinige Bewegung (Verschiebung) eines Körpers.

Alle diese Größen können durch einen Pfeil dargestellt werden. Wir nennen diese
Größen vektorielle Größen (Vektoren). Wir betrachten im Folgenden die geradlinige Verschiebung von Punkten im Raum, da sich
an diesem Beispiel die allen Vektoren gemeinsamen Gesetzmäßigkeiten besonders leicht einsehen lassen. Dabei beschränken wir uns in den
Abbildungen aus Gründen der Übersichtlichkeit auf eine ebene Darstellung, berücksichtigen jedoch in den Formeln und Gleichungen alle
drei Raumdimensionen.
Darstellung von Vektoren (Verschiebungen)

Wir stellen eine Verschiebung eines Punktes durch einen Pfeil Δr dar.
Die Länge des Pfeiles entspricht dem Betrag der Verschiebung, die Richtung des Pfeiles gibt die Richtung der Verschiebung an. Wir geben diese
Verschiebung zahlenmäßig durch die Koordinaten des Schiebungsvektors Δr an:

Zwei Schiebungen (Vektoren) sind gleich, wenn sie in Betrag und Richtung übereinstimmen. Gleiche
Vektoren stimmen in den entsprechenden Koordinaten überein. Ein Vektor ändert sich nicht, wenn man ihn verschiebt ohne ihn dabei zu drehen.
Der Anfangspunkt eines Vektors ist nicht von Bedeutung.
Betrag eines Vektors
Unter dem Betrag eines Vektors verstehen wir die Länge des Pfeils; sie ergibt sich mit Hilfe des
pythagoräischen Lehrsatzes.

Multiplikation eines Vektors mit einer Zahl (einem Skalar)
Es ist naheliegend, unter der Verschiebung 2·Δr eine Verschiebung
in der Richtung von Δr, jedoch um den doppelten Betrag zu verstehen. Analog wird die Verschiebung
−2·Δr eine Verschiebung in der entgegengesetzten Richtung von Δr um den
doppelten Betrag von Δr bedeuten.

Wir definieren daher: Das Produkt eines Vektors Δr mit einem
positiven (negativen) Skalar k ist ein Vektor mit gleicher (entgegengesetzter) Richtung und k-fachem Betrag von
Δr.

Insbesondere bedeutet der Vektor −Δr den zu
Δr entgegengesetzt gerichteten Vektor gleichen Betrages.
Summe und Differenz von Vektoren (Verschiebungen)
Wir schieben einen Punkt P um Δ1r nach P1 und von
dort um Δ2r nach P2. Die direkt von P nach P2 führende Schiebung ersetzt diese
beiden Schiebungen und wird als ihre Summe bezeichnet.

Aus der obigen Abbildung folgt

Die Koordinaten des Summenvektors erhält man durch Addition der entsprechenden Koordinaten der
Summanden. Für die Vektoraddition gilt das Kommutativgesetz

Vektoren werden graphisch addiert, indem man die Pfeile aneinanderfügt; der Summenvektor weist vom
Ausgangspunkt des ersten Summanden zur Spitze des letzten und schließt den von den Summanden gebildeten Vektorzug zum Vektorpolygon. Zwei von
einem Punkt aus aufgetragene Vektoren können auch nach der "Parallelogrammregel" addiert werden.

Für die Differenz d zweier Vektoren
Δ2r und Δ1r erhalten wir durch Anwendung der Regel


Komponentenzerlegung von Vektoren
Jeder Vektor kann auf beliebig viele Arten in zwei Summanden zerlegt werden.

Skalares (inneres) Produkt zweier Vektoren
Das skalare Produkt ordnet zwei gegebenen Vektoren a und
b eine Zahl (einen Skalar) zu.

Unter dem skalaren Produkt a·b zweier
Vektoren a und b verstehen wir das Produkt aus dem Betrag der
Normalprojektion ab des Vektors a auf den
Vektor b und dem Betrag des Vektors b, versehen mit den Vorzeichen +1, wenn der
Vektor ab in die gleiche Richtung wie der Vektor b zeigt, bzw. versehen mit
dem Vorzeichen −1, wenn der Vektor ab in entgegengesetzte Richtung wie der
Vektor b zeigt. Bezeichnet α den von den Vektoren a und
b eingeschlossenen Winkel, so gilt

Für das skalare Produkt gilt das Vertauschungsgesetz (Kommutativgesetz). Stehen die
Vektoren a und b aufeinander normal, so ist
a·b = 0. Sind in einem kartesischen Koordinatensystem zwei
Vektoren a und b durch ihre Koordinaten gegeben
so wird ihr skalares Produkt wie folgt berechnet:
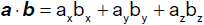
Vektorielles Produkt (Kreuzprodukt, Vektorprodukt, äußeres Produkt) zweier
Vektoren
Das vektorielle Produkt ist eine Verknüpfung im dreidimensionalen Raum, die zwei gegebenen
Vektoren a und b einen
Vektor c = a x b
zuordnet.
 |

Rechte-Hand-Regel
(Quelle: https://commons.wikimedia.org/wiki/File:RHR.svg, 22.06.2021) |
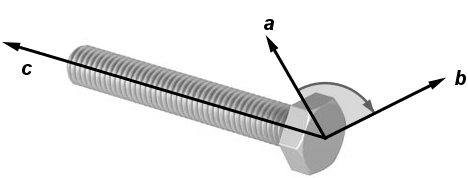
Rechtsschrauben-Regel
(Quelle: https://www.gebhardt-stahl.de/lufttechnik/luftkanalaussteifung/schrauben/, 23.05.2021) |
 |
Der Vektor c steht normal auf die von den
Vektoren a und b aufgespannte Ebene und bildet mit ihnen ein Rechtssystem. Der Betrag des
Vektors c entspricht dem Flächeninhalt des Parallelogramms, das von den Vektoren a
und b aufgespannt wird. Das vektorielle Produkt ist antikommutativ, d.h.

Bezeichnet α den von den Vektoren a und b
eingeschlossenen Winkel, so gilt

Sind die Vektoren a und b zueinander parallel, so
ist a x b = 0. Sind in einem kartesischen
Koordinatensystem zwei Vektoren a und b durch ihre Koordinaten gegeben
so wird ihr vektorielles Produkt wie folgt berechnet:
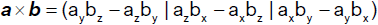
7. Kinematik (Bewegungslehre) - erster Teil
In der Kinematik werden Bewegungen von Körpern beschrieben, wobei die
Bewegungsursachen (Wechselwirkungen) außer Acht gelassen werden. Die Bewegung eines Körpers kann durchaus sehr kompliziert sein. So
beschreibt etwa ein Punkt auf der Peripherie eines waagrecht rollenden Rades (Kreis) eine sogenannte Zykloide, während sich die Radachse
geradlinig bewegt.
 |
 |
Noch komplizierter sind die Verhältnisse in strömenden Flüssigkeiten oder Gasen, da hier die
einzelnen Teile des Körpers nicht miteinander verbunden sind.
Grundsätzlich lässt sich jede Bewegung eines beliebigen Körpers beschreiben, indem wir uns diesen Körper in punktförmig
kleine Teile (Massenpunkte) zerlegt denken und die Bewegung des Gesamtkörpers durch die Bewegung jedes seiner Massenpunkte beschreiben.
Dabei ist ein Massenpunkt ein Teil des Körpers, dessen Ausdehnung bei der zu beschreibenden Bewegung vernachlässigt werden kann. Wie
"groß" ein Massenpunkt sein kann, hängt davon ab, welche Bewegung wir betrachten. So kann beispielsweise die Erde bei ihrer Bewegung um die
Sonne als ein Massenpunkt angesehen werden.
Die Freiheitsgrade der Bewegung
Wir schränken unsere Betrachtungen auf (ideal) starre Körper ein. Unter einem starren
Körper verstehen wir einen Körper, dessen Massenpunkte ihre gegenseitige Lage nicht ändern können; ein starrer Körper ist
also nicht verformbar. Die Lage eines starren Körpers kann auf zwei verschiedene Arten verändert werden.
Translation (Verschiebung) eines starren Körpers
Alle Massenpunkte bewegen sich dabei auf kongruenten (deckungsgleichen) Bahnen; jede im Körper
festgelegte Richtung bleibt dabei unverändert.
Rotation (Drehung) eines starren Körpers
Alle Massenpunkte bewegen sich auf zur Drehachse konzentrischen Kreisbahnen; die auf der Drehachse liegenden
Punkte bleiben in Ruhe. Im Körper festgelegte Richtungen, die zur Drehachse nicht parallel sind, werden bei der Rotation verändert.
In der folgenden Animation ist zum Vergleich links die Translation eines Körpers in einer Kreisbahn und
rechts die Rotation eines Körpers abgebildet.
Die Freiheitsgrade der Translation
Unser Raum ist dreidimensional. Das bedeutet, dass zur Angabe eines Punktes P in einem Koordinatensystem
stets drei Koordinaten nötig sind. Wir geben die Lage jedes Punktes P durch einen
Ortsvektor r = ( x | y | z ) an. Das ist ein Pfeil, der vom Ursprung O des
Koordinatensystems zum betreffenden Punkt weist. Die Koordinaten des Punktes P sind auch die Koordinaten des
Ortsvektors r.

Jede geradlinige Verschiebung eines Massenpunktes stellen wir durch einen
Schiebungsvektor Δr dar. Jede solche Verschiebung können wir uns in drei zu den Koordinatenachsen parallele
Schiebungen Δx, Δy und Δz zerlegt denken, die die Koordinaten des Schiebungsvektors angeben. Es gilt also
Δr = ( Δx | Δy | Δz ).
Da bei einer Translation eines starren Körpers alle Massenpunkte die gleiche Verschiebung erfahren, gibt ein Schiebungsvektor die Verschiebung
aller Massenpunkte und damit die Verschiebung des gesamten Körpers an. Da sich jede solche Schiebung aus drei zu den Koordinatenachsen parallelen
Schiebungen zusammensetzen lässt, sagen wir: "Ein starrer Körper hat (wie ein Massenpunkt)
drei Freiheitsgrade der Translation."
Die Freiheitsgrade der Rotation
Zur vollständigen Angabe der Lage eines starren Körpers genügen drei Koordinaten jedoch nicht.
Legen wir nämlich einen Punkt P des Körpers durch seine drei Lagekoordinaten fest, so kann der starre Körper noch um diesen Punkt
gedreht werden und damit seine Orientierung ohne Änderung von P verändern.
So wie wir jede Verschiebung im Raum aus drei Schiebungen parallel zu den drei Koordinatenachsen zusammensetzen können, so können wir jede
Drehung aus drei Drehungen um drei Achsen zusammensetzen. Wir sagen daher: "Ein starrer Körper hat drei
Freiheitsgrade der Rotation." Davon wird z.B. bei einem kardanisch aufgehängten Körper Gebrauch gemacht. Dieser Körper kann
um einen festen Punkt in jede beliebige Orientierung gedreht werden.

Gyroskop
(Quelle: https://www.dorotheum.com/de/l/476446/, 31.05.2021)
Insgesamt besitzt ein starrer Körper also sechs Freiheitsgrade der Bewegung. Da bei einem Massenpunkt
keine Richtungen angegeben werden können, ist es sinnlos, von der Drehung eines Massenpunktes zu sprechen. Ein Massenpunkt besitzt daher nur drei
Freiheitsgrade der Bewegung, nämlich die drei Freiheitsgrade der Translation.
Die gleichförmige Translation
Wir bezeichnen eine Translation als gleichförmig, wenn sie entlang einer geraden Bahn erfolgt und der
Körper in gleichen Zeiten gleich gerichtete Wegstrecken zurücklegt. Bei der Bewegung eines freien Körpers in einem Inertialsystem ist
das der Fall.
In der obigen Abbildung (Animation) ist die Verschiebung je Sekunde durch den
Vektor v dargestellt. In 2, 3, 4, ... Sekunden ist die
Verschiebung Δr 2, 3, 4, ... mal so groß. Ein Massenpunkt (Körper)
bewegt sich daher gleichförmig, wenn die Verschiebung Δr zur benötigten Zeit Δt direkt
proportional ist. Es gilt

Der Quotient
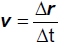
heißt Geschwindigkeit der gleichförmigen Translation. Die Vektorgleichung

bringt die konstante Bewegungsrichtung zum Ausdruck, denn das Produkt des
Geschwindigkeitsvektors v mit dem Skalar Δt hat stets die konstante Richtung von
v. Da gleiche Vektoren auch gleiche Beträge (Längen) haben, ergibt sich aus dieser Vektorgleichung auch eine
Betragsgleichung für die zurückgelegte Wegstrecke, die wir mit Δs bezeichnen.

Zur Beschreibung der gleichförmigen Translation können wir so wie bei allen geradlinigen Bewegungen
auf die Verwendung von Vektoren verzichten, da wir die Bahn der Bewegung durch eine entsprechende Wahl des Koordinatensystems stets in die
Zahlengerade (x-Achse) legen und alle vorkommenden Größen durch reelle Zahlen ausdrücken können, die auf der Zahlengeraden
durch gerichtete Strecken dargestellt werden. Aus der Gleichung
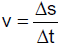
ergibt sich für die kohärente Maßeinheit der Geschwindigkeit

Eine gebräuchliche inkohärente Einheit ist

Diagramme

Das linke Diagramm in der obigen Abbildung zeigt ein Zeit-Weg-Diagramm. Es gibt für jedes
Zeitintervall Δt den Betrag der zurückgelegten Wegstrecke Δs an. Der rechte Teil der Abbildung stellt das zugehörige
Zeit-Geschwindigkeit-Diagramm dar. In diesem Diagramm ist der Betrag der Geschwindigkeit zu jedem Zeitpunkt t aufgetragen. Der Betrag der
Geschwindigkeit ist durch die Steigung im Zeit-Weg-Diagramm gegeben. Die im Zeitintervall Δt zurückgelegte Wegstrecke Δs
ist zahlenmäßig gleich der Fläche zwischen der Geschwindigkeitsgeraden und der Zeitachse.
Aus diesen beiden Diagrammen kann jedoch nicht abgelesen werden, ob sich der betreffende Körper auf der Zahlengeraden nach links oder rechts
bewegt und in welchem Punkt die Bewegung beginnt. Das ist aus den folgenden Diagrammen ersichtlich.

Das linke Diagramm in der Abbildung zeigt ein Zeit-Weg-Diagramm der gleichförmigen Translation zweier
Körper A und B entlang der Zahlengeraden. Hier ist jedoch im Gegensatz zu vorher nicht die betragsmäßige
Verschiebung Δs der beiden Körper in einem Zeitintervall Δt, sondern die Wegkoordinate, die wir mit s bezeichnen, zu jedem
Zeitpunkt t angegeben. Körper A bewegt sich nach rechts, Körper B nach links. Beide Körper beginnen ihre Bewegung nicht
im Nullpunkt. Das rechte Diagramm zeigt das zugehörige Zeit-Geschwindigkeit-Diagramm. Dabei ist die Bewegungsrichtung der beiden Körper
durch das Vorzeichen der Geschwindigkeit gegeben. Für die Wegkoordinate s(t) gilt

Dass Wegstrecken durch Flächen im Zeit-Geschwindigkeit-Diagramm dargestellt sind, gilt nicht nur
für die gleichförmige Translation, sondern für alle geradlinigen Bewegungen. Wir wollen dies an einem einfachen Beispiel verdeutlichen.
Dazu betrachten wir einen Körper, der sich zunächst 2 Sekunden mit der Geschwindigkeit 5 m/s auf der Zahlengeraden
gleichförmig nach rechts und anschließend 4 Sekunden mit der Geschwindigkeit 2 m/s gleichförmig nach links bewegt. Die
Bewegung dieses Körpers ist aus zwei gleichförmigen Translationen zusammengesetzt und soll im Nullpunkt beginnen. Die folgende Animation
zeigt diese Bewegung und das zugehörige Zeit-Geschwindigkeit-Diagramm.
 |
 |
Die beiden Rechteckflächen im Zeit-Geschwindigkeit-Diagramm ergeben addiert
10 + 8 = 18 m und damit die insgesamt zurückgelegte Wegstrecke im
Zeitintervall [ 0 s ; 6 s ]. Wird die Fläche des unterhalb der Zeitachse gelegenen Rechtecks jedoch negativ
gerechnet, so erhalten wir 10 - 8 = 2 m, was der Änderung der Wegkoordinate im betrachteten Zeitintervall
entspricht.
 |
Allgemein gilt für die geradlinige Bewegung eines Körpers mit
Geschwindigkeitsfunktion v (t):
Die Änderung der Wegkoordinate s im
Zeitintervall [ t1 ; t2 ] ist gegeben durch
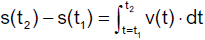
Für die gleichförmige Translation erhalten wir

Die im Zeitintervall [ t1 ; t2 ] zurückgelegte
Wegstrecke Δs ist gegeben durch

|
|
Die ungleichförmige Translation auf gerader Bahn
Jede nicht gleichförmige Translation heißt ungleichförmig. Ungleichförmig ist eine
Translation einerseits immer dann, wenn sie auf krummer Bahn erfolgt, da sich hier die Bewegungsrichtung ändert. Andererseits ist eine
geradlinige Bewegung ungleichförmig, wenn die zurückgelegte Wegstrecke nicht zur dafür benötigten Zeit proportional ist, d.h. sich
der Betrag der Geschwindigkeit des Körpers ändert. In beiden Fällen nennen wir die Bewegung beschleunigt.
Wir betrachten in diesem Abschnitt ausschließlich ungleichförmige Translationen auf gerader Bahn. Mit krummlinigen
Bewegungen (z.B. Wurfbewegungen) werden wir uns in einem späteren Abschnitt befassen.
Die gleichmäßig beschleunigte Translation
Eine Translation heißt gleichmäßig beschleunigt, wenn die
Geschwindigkeitsänderung Δv zur dafür benötigten Zeit Δt proportional ist.

Der Quotient

heißt die Beschleunigung der gleichmäßig beschleunigten Translation. Die Beschleunigung ist
ein Vektor, der in die Richtung der Geschwindigkeitsänderung Δv weist und die Änderung der
Geschwindigkeit pro Zeiteinheit angibt. Da wir nur geradlinige Bewegungen betrachten, können wir wie bei der gleichförmigen Translation auf
die Verwendung von Vektoren verzichten und zu Betragsgleichungen übergehen.

Aus dieser Gleichung erhalten wir für die kohärente Einheit der Beschleunigung

Für eine aus dem Ruhezustand im Nullpunkt beginnende gleichmäßig beschleunigte Translation
auf gerader Bahn gilt für t ≥ 0
| Beschleunigung a |
Geschwindigkeit v zum Zeitpunkt t |
Wegkoordinate s zum Zeitpunkt t |
 |
 |
 |
 |
 |
 |
Für t = 0 ist v(t) = 0 und s(t) = 0. Somit beginnt die Bewegung im
Nullpunkt aus dem Ruhezustand. Da die Beschleunigung a konstant ist, gilt für ein beliebiges
Zeitintervall [ t1 ; t2 ]

Daraus folgt, dass die Geschwindigkeitsänderung zu der dafür benötigten Zeit proportional ist.
Um den Zusammenhang zwischen der Weg- und der Geschwindigkeitsfunktion zu zeigen, betrachten wir die folgende Abbildung.

Der Quotient

ist die mittlere Änderungsrate der Wegkoordinate im
Zeitintervall [ t ; t+Δt ] und wird als mittlere Geschwindigkeit bezeichnet. Sie kommt als Anstieg der Sekante im
Zeit-Weg-Diagramm zum Ausdruck. Die mittlere Geschwindigkeit wird von der Momentangeschwindigkeit (momentane Änderungsrate der
Wegkoordinate) im Zeitpunkt t umso weniger abweichen, je kleiner wir das Zeitintervall wählen. Für Δt → 0 geht die
Sekante in die Tangente über und wir erhalten für die Momentangeschwindigkeit im Zeitpunkt t

Allgemein gilt: Die Momentangeschwindigkeit ist ein Vektor, der stets in die jeweilige
Bewegungsrichtung (also in die Richtung der Bahntangente) weist. Das bringt die folgende Vektorgleichung zum Ausdruck.

Die zurückgelegte Wegstrecke entspricht der Fläche zwischen der Zeit-Geschwindigkeit-Kurve und der
Zeitachse im Zeit-Geschwindigkeit-Diagramm; die Geschwindigkeit entspricht der Fläche zwischen der Zeit-Beschleunigung-Kurve und der Zeitachse im
Zeit-Beschleunigung-Diagramm. Die Beschleunigung steht mit der Geschwindigkeit in genau demselben Zusammenhang wie die Geschwindigkeit mit dem
Weg.

Die folgende Animation zeigt eine gleichmäßig beschleunigte Translation auf gerader Bahn und die
drei zugehörigen Diagramme.
Die Bremsstrecke eines Fahrzeugs
Wir betrachten ein Fahrzeug, das sich gleichförmig mit der Geschwindigkeit v0 bewegt. Ab
dem Zeitpunkt t1 verringert es gleichmäßig seine Geschwindigkeit und kommt zum Zeitpunkt t2 zum
Stillstand.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/auto_2554896, 16.05.2021) |
 |
Die Bremsverzögerung a (d.h. die Abnahme der Geschwindigkeit pro Zeiteinheit) ist gleich dem
Betrag der Steigung der Geschwindigkeitsfunktion im Zeitintervall [ t1 ; t2 ] und beträgt

Die Bremsstrecke ΔsB entspricht zahlenmäßig der Dreiecksfläche unter
der Geschwindigkeitsfunktion.

Einsetzen für die Bremszeit ΔtB ergibt

Die Bremsstrecke wächst also mit dem Quadrat der Geschwindigkeit, einer Tatsache, der sich jeder
Fahrzeuglenker bewusst sein sollte.
8. Die Grundgröße Masse
Wir haben in Kapitel fünf festgestellt, dass alle Körper träge sind und dazu das
Beharrungsgesetz (Trägheitsgesetz) formuliert. Die Ursache für die Trägheit ist die allen Körpern anhaftende Eigenschaft
der (trägen) Masse. Wir führen die Masse m als physikalische Grundgröße ein und haben daher Messvorschriften für
die Massenmessung zu erstellen. Wir legen dabei unseren Betrachtungen ein Inertialsystem zugrunde und betrachten stets nur zwei Körper, die
miteinander in Wechselwirkung treten können und ein abgeschlossenes System bilden sollen. Wir definieren dazu: Zwei Körper bilden ein
abgeschlossenes System, wenn sie mit keinem dritten Körper in Wechselwirkung treten können. Wir betrachten dazu einige "Versuche".
Zwischen zwei gleichen, mit einem Faden verbundenen Spielzeugwagen ist eine Blattfeder gespannt. Nach Durchtrennen des Fadens kommen sie in
entgegengesetzte Richtungen in Bewegung (elastische Wechselwirkung). Dabei erfahren die beiden Wagen entgegengesetzt gleiche
Geschwindigkeitsänderungen.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021) |
 |
Wir versehen die beiden Wagen jeweils mit der gleichen Anzahl von zusätzlichen gleichartigen
"Gewichtsstücken". Die Geschwindigkeitsänderungen sind jetzt betragsmäßig kleiner, jedoch immer entgegengesetzt gleich.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Wir ersetzen die elastische Wechselwirkung durch eine magnetische Wechselwirkung (zwei Magnete mit
gleichen Polen einander zugewandt). Wieder ergeben sich entgegengesetzt gleiche Geschwindigkeitsänderungen.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Wir versehen jetzt nur einen der beiden Wagen mit zusätzlichen Gewichtsstücken. Die
Geschwindigkeitsänderungen sind wieder entgegengesetzt gerichtet, jedoch nicht mehr betragsmäßig gleich. Der Wagen mit den
zusätzlichen Gewichtsstücken erfährt die kleinere Geschwindigkeitsänderung.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Diese Überlegungen (Versuche) zeigen: Zwei Körper, die ein abgeschlossenes System bilden,
erfahren bei jeder Wechselwirkung entgegengesetzt gerichtete Geschwindigkeitsänderungen. Haben diese Geschwindigkeitsänderungen bei
irgendeiner Wechselwirkung gleichen Betrag, so ist das bei jeder Wechselwirkung der Fall. Nur durch Veränderung eines der beiden Körper kann
das Geschwindigkeitsverhältnis geändert werden.
Das konstante Verhältnis der Geschwindigkeitsänderungen muss daher durch eine Eigenschaft der Körper bedingt sein und nicht durch die
Art der Wechselwirkung. Diese Eigenschaft nennen wir die Masse der Körper. Die Masse ist eine skalare Größe.
Definition der Massengleichheit
| |
Zwei Körper, die ein abgeschlossenes System bilden, haben genau dann gleiche Masse,
wenn sie bei irgendeiner Wechselwirkung in einem Inertialsystem entgegengesetzt gleiche Geschwindigkeitsänderungen erfahren. |
|

Definition der Massenvielfachheit
Die obigen Überlegungen haben gezeigt, dass die an zwei Körpern eines abgeschlossenen Systems
auftretenden Beträge der Geschwindigkeitsänderungen in einem von der Art der Wechselwirkung unabhängigen konstanten Verhältnis
stehen. Dabei erfährt der Körper (Wagen) mit den zusätzlichen Gewichtsstücken die kleinere Geschwindigkeitsänderung. Er
hat die größere Trägheit. Wir ordnen im daher auch die größere Masse zu.
| |
Die Massen m1 und m2 zweier Körper, die ein
abgeschlossenes System bilden, verhalten sich umgekehrt wie die bei irgendeiner Wechselwirkung in einem Inertialsystem auftretenden Beträge der
Geschwindigkeitsänderungen. Der Körper mit der 2, 3, 4, ... fachen Masse erfährt eine
1/2, 1/3, 1/4, ... so große Geschwindigkeitsänderung. |
|

Die Einheit der Masse
Die im Internationalen Einheitensystem (SI) verwendete Maßeinheit für die Masse ist das
Kilogramm (kg). Im Rahmen der Einführung des metrischen Maßsystems im Jahr 1791 wurde 1 kg als die Masse von
1 dm3 Wasser bei 4°C definiert. Nach dieser Definition wurde der Internationale Kilogrammprototyp (Urkilogramm)
gefertigt, ein Zylinder aus einer Platin-Iridium-Legierung mit 39 Millimeter Höhe und 39 Millimeter Durchmesser. Spätere
Überprüfungen zeigten, dass die Masse dieses Urkilogrammstücks etwas zu groß ausgefallen war. Ab 1895 galt daher die folgende
Definition.
| |
Die Einheit der Masse ist das Kilogramm (kg). Ein Kilogramm ist die Masse des in
Sèvres bei Paris aufbewahrten Internationalen Kilogrammprototyps. |
|

Eine Kopie des Urkilogrammstücks neben einer Kopie des Urmeterstabes
(Quelle: http://www.wiese.itp.unibe.ch/public/masse.pdf, 01.06.2021)
Bis 2003 wurden 84 Kilogrammprototypen hergestellt, die teilweise als nationale Kilogrammprototypen
dienten. Vergleiche der nationalen mit dem Internationalen Kilogrammprototyp (Nachprüfungen) haben gezeigt, dass das Urkilogramm im
Vergleich zu den Kopien in 100 Jahren um ca. 50 Mikrogramm leichter geworden ist. Die Ursache dafür ist nicht bekannt. Im
Jahr 2019 wurde daher das Kilogramm über eine Naturkonstante neu definiert.
| |
Die Einheit für die Masse ist das Kilogramm (kg). Das Kilogramm ist definiert,
indem für die Planck-Konstante h der Zahlenwert 6,626 070 15 x 10−34 festgelegt wird, ausgedrückt
in der Einheit J·s, die gleich kg·m2·s−1 ist, wobei der Meter und die Sekunde mittels c und
ΔνCs definiert sind. |
|
Die Dichte der Körper
Unter der Dichte ρ eines homogenen (d.h. überall gleich beschaffenen) Körpers
verstehen wir seine Masse pro Volumseinheit:

Daraus ergibt sich für die kohärente Einheit der Dichte:

Die Dichte ist eine wichtige Materialkonstante. Die folgende Tabelle zeigt eine Übersicht über die
Dichte einiger Stoffe in kg/m3.

9. Masse und Kraft
Der Begriff "Kraft" ist uns aus dem Alltag geläufig. Wir sprechen von Muskelkraft, Motorkraft und
Geisteskraft. In der Physik bedarf es jedoch einer genauen Definition dieses Begriffs und entsprechender Messvorschriften.
Die Größe einer Kraft kann stets nur an ihren Wirkungen beurteilt werden. Bei der Kraftmessung mit einer Federwaage wird die Verformung
eines elastischen Körpers als Maß der Kraft benutzt. Wir bezeichnen diese Kraftmessung als statische Kraftmessung.
Die dynamische Kraftdefinition
Bei den Versuchen zur Wechselwirkung zwischen Körpern war stets etwas wirksam, das wir als Kraft
bezeichnen. Als Wirkung dieser Kräfte wurde aber keine Verformung eines Körpers beobachtet, sondern eine Beschleunigung der in
Wechselwirkung stehenden Körper. Aus Erfahrung wissen wir, dass zur Beschleunigung eines Körpers oft große Kräfte nötig
sind. Wir brauchen umso größere Kraft, je größere Masse der beschleunigte Körper hat und je stärker man ihn
beschleunigt. Wir definieren daher:
| |
Die auf einen Körper wirkende Kraft F ist das
Produkt aus der Masse m des Körpers und der an ihm erzielten Beschleunigung a. |
|
| |
 |
|
dynamische Kraftdefinition |
|
Die dynamische Kraftdefinition wurde erstmals von Isaac Newton in seiner Philosophiae naturalis principia
mathematica 1687 formuliert: "Mutationem motus proportionalem esse vi motrici impressae, et fieri secundum
lineam rectam qua vis illa imprimitur."
Nach der obigen Definition ist die Kraft ein Vektor. Die Richtung der Kraft ist die Richtung der
Beschleunigung, der Betrag der Kraft ist m-mal so groß wie der Betrag der Beschleunigung. Für Kräfte gelten alle Regeln, die für
Vektoren gelten. Aus der Definitionsgleichung ergibt sich für die kohärente Einheit der Kraft

| |
Die Einheit der Kraft ist 1 kg·m·s−2 und heißt
1 Newton (1 N). 1 Newton ist jene Kraft, die einem Körper der Masse 1 kg die
Beschleunigung 1 m·s−2 erteilt. |
|
Die Übereinstimmung des dynamisch definierten Kraftbegriffes mit dem statischen zeigen die folgenden
Versuche.
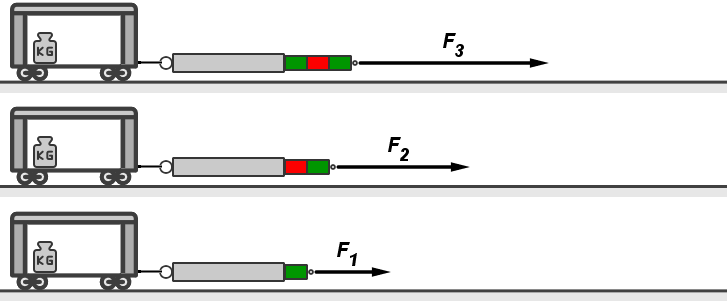
(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
An einem Spielzeugwagen ist eine Federwaage befestigt. Ziehen wir schwach an der Federwaage - sie zeigt nur
geringe Dehnung, also nur geringe Kraft im Sinne des statischen Kraftbegriffes - so zeigt der Wagen nur geringe Beschleunigung. Es ist also auch die
dynamisch beurteilte Kraft klein. Starkes Ziehen zeigt eine starke Dehnung und damit eine statisch große Kraft; der Wagen wird bei gleicher
Masse stärker beschleunigt, es ist also auch die dynamisch beurteilte Kraft groß.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Ziehen wir stets mit gleicher statisch beurteilter Kraft (konstante Dehnung der Federwaage), so sinkt
mit größer werdender Masse des Wagens die Beschleunigung in Übereinstimmung mit der dynamischen Kraftdefinition.
Folgerungen aus der dynamischen Kraftdefinition
a) Aus a = 0 folgt
F = m·a = 0; d.h. verharrt ein Körper im
Zustand der Ruhe oder im Zustand gleichförmiger Bewegung (a = 0), so ist die
an ihm wirkende Kraft F Null. Das ist das Beharrungsgesetz in einer anderen Formulierung.
b) Aus a = konst. und m = konst. folgt
F = m·a = konst.; d.h. bewegt sich ein Körper
gleichmäßig beschleunigt, so wirkt auf ihn eine (nach Betrag und Richtung) konstante Kraft.
c) Wir wollen die Kräfte vergleichen, die auf zwei in Wechselwirkung tretende Körper wirken. Dazu
müssen wir ihre Beschleunigungen ermitteln und diese mit ihrer Masse multiplizieren. Aus der Beziehung

folgt

bzw.

Wir dividieren durch die für beide Körper gleiche Dauer der Wechselwirkung Δt und
erhalten

oder

Δv1/Δt und
Δv2/Δt sind die mittleren Beschleunigungen der Massen m1 bzw. m2. Damit
erhalten wir

Wir lassen Δt gegen Null streben; dann streben die mittleren Beschleunigungen gegen die
Momentanbeschleunigungen und es gilt

bzw.

Das heißt

oder

Das ist das Gegenwirkungsgesetz. Es besagt:
| |
Auf zwei in Wechselwirkung stehende Körper wirken stets entgegengesetzt gerichtete
Kräfte (Actio est Reactio). Die Summe der bei einer Wechselwirkung von den beteiligten Körpern aufeinander ausgeübten Kräfte
ist stets Null. Mit anderen Worten: In einem abgeschlossenen System ist die Summe der "inneren Kräfte" stets Null. |
|
Isaac Newton: "Actioni contrariam semper et aequalem esse reactionem: sive
corporum duorum actiones in se mutuo semper esse aequales et in partes contrarias dirigi." (Philosophiae naturalis principia mathematica
1687)
Freier Fall und Gewicht
Zwischen der Erde und den in ihrer Nähe befindlichen Körpern besteht eine Wechselwirkung, die wir
als Gravitation bezeichnen. Die auf einen Körper ausgeübte Gravitationskraft heißt die Gewichtskraft bzw. das Gewicht des
Körpers. Um das Gewicht eines Körpers zu messen, ist es nach der dynamischen Kraftdefinition notwendig, festzustellen, wie stark dieser
Körper durch die Erdanziehung beschleunigt wird, wenn er frei beweglich ist. Wir müssen daher die Bewegung des Körpers beim
"freien Fall" untersuchen.
Dabei können wir auf der Erdoberfläche eine bemerkenswerte Tatsache beobachten. Lässt man die verschiedensten Objekte unter dem
Einfluss der Gravitation zu Boden fallen, dann stellt man fest, dass sie alle in der gleichen Weise beschleunigt werden. Zumindest gilt das, wenn man
die Effekte der Luftreibung (Luftwiderstand) ausschaltet, indem man die Fallversuche etwa in einer Vakuumkammer durchführt.

(Quelle: Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-icon/feder_3230622, 04.04.2021
Icons erstellt von Pixel perfect,
https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)
 |

(Quelle: Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-icon/feder_3230622, 04.04.2021
Icons erstellt von Pixel perfect,
https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)
 |
Bis ins Mittelalter war man nach der Lehre des Aristoteles der Meinung, dass ein Körper umso schneller
fällt, je schwerer er ist (je größere Masse er hat). Erst Galileo Galilei widerlegte diese Meinung und ersann dazu das folgende
Gedankenexperiment.

Die Abbildung zeigt drei Körper A, B und C. Körper C entsteht durch
Anfügen von Körper A unterhalb von Körper B. Wenn schwerere Körper schneller fallen, dann sollte Körper C
schneller fallen als Körper B und Körper B schneller fallen als Körper A. Andererseits müsste aber
Körper C langsamer als Körper B fallen, da der untere Teilkörper den oberen Teilkörper beim Fall bremst.
Ohne die störende Wechselwirkung mit der Luft (Luftwiderstand) erfahren alle frei fallenden
Körper am selben Ort auf der Erde die gleiche konstante Beschleunigung. Diese Beschleunigung heißt
Erdbeschleunigung g. Ihr Wert hängt etwas von der geographischen Lage ab. Als Normwert wird die in Sèvres
bei Paris herrschende Erdbeschleunigung definiert.

Ein frei fallender Körper führt eine gleichmäßig beschleunigte Translation aus. Für
einen bestimmten Ort auf der Erde gilt
| Erdbeschleunigung |
Fallgeschwindigkeit |
Fallhöhe |
 |
 |
 |
 |
 |
 |
Auf den frei fallenden Körper der Masse m wirkt daher eine konstante
Kraft G (Gewicht des Körpers).

Das Gewicht des Körpers ändert sich bei geringem Höhenunterschied nicht messbar. Es ist zur
Masse m direkt proportional und von der Geschwindigkeit des Körpers unabhängig. Der ruhende Körper hat dasselbe Gewicht wie der
fallende Körper. Kräfte können daher durch das Gewicht von Körpern realisiert werden.
Die folgende Abbildung (Animation) zeigt das Zeit-Weg-Diagramm eines frei fallenden Körpers. Dabei ist die Fallhöhe nach unten
aufgetragen.
Da Körper gleicher Masse am selben Ort gleiches Gewicht haben, können wir die Masse von
Körpern durch ihre Gewichte vergleichen. Aus G1 = m1·g
und
G2 = m2·g folgt m1 = m2,
wenn G1 = G2. Betrachten wir dazu eine Balkenwaage.

(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021
Icons erstellt von smalllikeart, https://www.flaticon.com/de/kostenloses-icon/sack_2410641, 14.06.2021) |
 |
Es gilt: Zwei Körper haben die gleiche Masse, wenn auf einer im Gleichgewicht befindlichen Balkenwaage
nach dem Auflegen der Körper und nach dem Vertauschen der beiden Körper Gleichgewicht bestehen bleibt.
10. Kinematik (Bewegungslehre) - zweiter Teil
Im ersten Teil der Bewegungslehre haben wir uns auf geradlinige Translationen beschränkt. Jetzt soll
gezeigt werden, wie sich ein Körper verhält, wenn er mehrere Bewegungen gleichzeitig ausführt. Betrachten wir dazu ein einfaches
Beispiel.
Ein Boot überquert einen Fluss. In einem ruhenden Gewässer legt das Boot je Zeiteinheit die
Strecke vBoot zurück. Wegen der Fließgeschwindigkeit des Flusses wird das Boot je Zeiteinheit jedoch um die
Strecke vFluss flussabwärts getrieben. Die Erfahrung zeigt, dass die je Zeiteinheit zurückgelegte Strecke v durch die
Vektorsumme aus vBoot und vFluss gegeben ist. Das entspricht zwei Verschiebungen, die hintereinander ausgeführt werden. Die
beiden Bewegungen des Bootes stören einander offenbar nicht. Das ist eine wichtige Feststellung, die wir als allgemeingültig betrachten. Wir
nennen sie das
Unabhängigkeitsprinzip für Bewegungen
| |
Führt ein Körper mehrere Bewegungen gleichzeitig aus, so beeinflussen diese
Bewegungen einander nicht. Der Körper kommt daher bei gleichzeitiger Ausführung mehrerer Bewegungen nach jeder Zeit t genau in jene
Lage, die er bei aufeinanderfolgender Ausführung der Teilbewegungen während derselben Zeit t erreicht hätte. |
|
Ein schönes Beispiel für die unabhängige Überlagerung von Bewegungen sind die sogenannten
Lissajous-Figuren, benannt nach dem französischen Physiker Jules Antoine Lissajous (1822 – 1880). Sie entstehen
durch die Überlagerung zweier harmonischer, rechtwinklig zueinander stehender Schwingungen.
Das Unabhängigkeitsprinzip für Bewegungen soll jetzt bei krummlinigen Translationen, die sich in
solche auf gerader Bahn zerlegen lassen, angewendet werden.
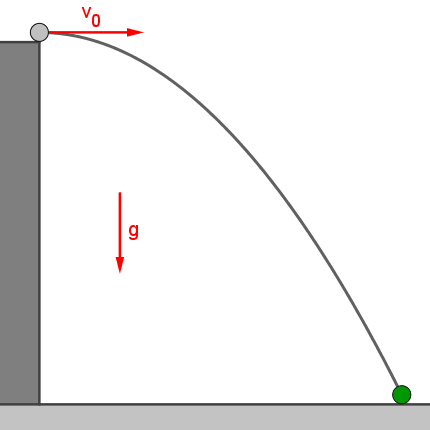
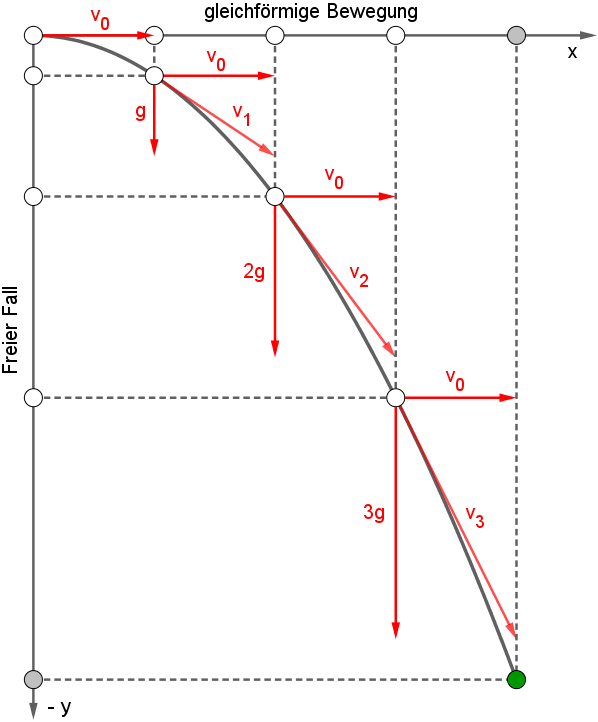
Der horizontale Wurf
Ein Körper wird horizontal mit der Geschwindigkeit v0 abgeworfen. Die folgende
Abbildung (Animation) zeigt die Bahnkurve dieser Bewegung.
 |
 |
Zur Beschreibung des horizontalen Wurfes müssen wir zuerst die Lage des Körpers zu jedem
Zeitpunkt t angeben. Dazu legen wir ein rechtwinkeliges Koordinatensystem mit dem Ursprung in den Abwurfpunkt und geben zu jedem Zeitpunkt t
die Abszisse x(t) und die Ordinate y(t) an. Das bedeutet die Zerlegung der Bewegung in einen horizontalen Anteil (Horizontalkomponente)
und einen vertikalen Anteil (Vertikalkomponente). x und y sind die Koordinaten des Ortsvektors für den geworfenen "Massenpunkt".
Nach dem Unabhängigkeitsprinzip bewegt sich der Körper entlang der Horizontalen gleichförmig mit der
Geschwindigkeit v0, ebenso wie er sich ohne die gleichzeitige Fallbewegung bewegen müsste, da keine Kraft in horizontaler
Richtung wirkt. Dasselbe gilt auch für die Fallbewegung: Der horizontal geworfene Körper legt in der Lotrechten genau dieselben Wege
zurück, wie der nur frei fallende; seine horizontale Bewegung stört seine Fallbewegung nicht.
 |
 |
Mit Hilfe des Unabhängigkeitsprinzips können wir nun die Lage des horizontal geworfenen
Körpers für jeden Zeitpunkt t konstruieren. Zum Zeitpunkt t befindet sich der Körper in einem Punkt mit den Koordinaten
 |
gleichförmige Translation in x-Richtung |
 |
 |
 |
freier Fall in y-Richtung |
Der Ortsvektor r(t) des geworfenen "Massenpunktes" ist daher gegeben durch

Wegen

gilt

Die Bahnkurve des horizontalen Wurfes ist somit eine Parabel. Die obige Abbildung zeigt auch die Konstruktion
der Geschwindigkeit in einigen Punkten der Bahnkurve aus den entsprechenden Horizontal- und Vertikalkomponenten. Die "tatsächlichen"
Geschwindigkeiten ergeben sich durch vektorielle Addition dieser Komponenten. Ihre Richtung ist stets tangential zur Bahnkurve. Für die
Geschwindigkeit beim horizontalen Wurf gilt:
 |
gleichförmige Bewegung in horizontaler Richtung |
 |
 |
 |
freier Fall in vertikaler Richtung |
Der Geschwindigkeitsvektor ist daher durch

und sein Betrag durch

gegeben.
 |
Die Abbildung links zeigt einen sogenannten Hodographen des horizontalen Wurfes. Dabei ist
ein Hodograph einer Bewegung die Menge der Endpunkte der von einem festen Punkt aus abgetragenen Geschwindigkeitsvektoren. Da die Horizontalkomponente
der Geschwindigkeit konstant ist, liegen alle Spitzen der Geschwindigkeitsvektoren auf einer Geraden. Man erkennt, dass die Geschwindigkeit in
gleichen Zeitintervallen gleiche Änderung erfährt; es liegt daher eine gleichmäßig beschleunigte Translation mit der
Erdbeschleunigung g vor. Eine gleichmäßig beschleunigte Translation muss also keineswegs (wie eine
gleichförmige Translation) auf gerader Bahn erfolgen. |
|
Der lotrechte Wurf
Ein Körper wird lotrecht (in Richtung der y-Achse) mit einer
Anfangsgeschwindigkeit v0 geworfen. Ohne Schwerkraft würde er gleichförmig mit
v0 steigen; infolge der Schwerkraft führt er aber als zweite Bewegung einen freien Fall aus. Die folgende
Abbildung (Animation) zeigt das Zeit-Weg-Diagramm und das Zeit-Geschwindigkeit-Diagramm eines lotrechten Wurfes.
Es gilt:
 |
Wegkoordinate (Steighöhe) |
 |
 |
 |
Geschwindigkeit |
 |
 |
 |
Beschleunigung |
Nach der sogenannten Steigzeit tH erreicht der Körper die maximale
Höhe H (Scheitelhöhe). Seine Geschwindigkeit ist zu diesem Zeitpunkt Null. Daraus folgt für die Steigzeit

Durch Einsetzen erhalten wir für die Scheitelhöhe H

Der schiefe Wurf
Ein Körper wird unter einem
Winkel α (0° < α < 90°) gegen die Horizontale mit der
Abwurfgeschwindigkeit v0 vom Boden abgeworfen. Die folgende Abbildung (Animation) zeigt die Bahnkurve
einer solchen Bewegung.
Zur Beschreibung des schiefen Wurfes müssen wir die Lage des Körpers zu jedem Zeitpunkt t
angeben. Dazu legen wir ein rechtwinkeliges Koordinatensystem mit dem Ursprung in den Abwurfpunkt und geben zu jedem Zeitpunkt t die
Koordinaten x(t) und y(t) des Körpers an. Wie aus der Abbildung ersichtlich, lässt sich der schiefe Wurf in zwei geradlinige
Bewegungen (Komponenten) zerlegen. Die Horizontalkomponente ist eine gleichförmige Bewegung, die Vertikalkomponente ein lotrechter Wurf. Zur
Bestimmung der jeweiligen Geschwindigkeiten dieser beiden Bewegungen betrachten wir eine Zerlegung des
Geschwindigkeitsvektors v0.

Aus der Abbildung entnehmen wir für die gleichförmige Bewegung in x-Richtung die
Geschwindigkeit vx = v0·cos(α) und für den lotrechten Wurf in y-Richtung die
Abwurfgeschwindigkeit vy = v0·cos(α). Damit ergibt sich für die Koordinaten x(t) und y(t)
des Körpers zum Zeitpunkt t
Für die Geschwindigkeitskomponenten erhalten wir
Für die Beschleunigung gilt

Somit sind alle Wurfbewegungen gleichmäßig beschleunigte Bewegungen. Um die Gleichung der
Bahnkurve zu erhalten, eliminieren wir die Variable t. Einsetzen von

in y ergibt
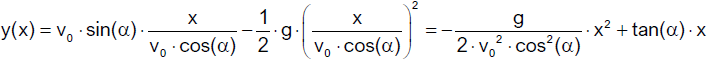
Die Bahnkurve ist daher eine Parabel (Wurfparabel). Um die Wurfweite W zu erhalten, müssen wir
den rechten Schnittpunkt der Wurfparabel mit der x-Achse bestimmen.

Damit erhalten wir für die Wurfweite und die Scheitelhöhe des schiefen Wurfes

Für 0° < α < 90° ist
0 < sin(2α) ≤ 1. Die maximale Wurfweite erhalten wir für sin(2α) = 1, d.h.
2α = 90° bzw. α = 45°. Für
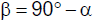
gilt

Komplementäre Abwurfwinkel ergeben somit gleiche Wurfweite.
11. Kräfte
Das statische Gleichgewicht der Kräfte
Wirken auf einen Körper (Massenpunkt) der Masse m mehrere Kräfte ein, so erfährt er
durch jede eine Beschleunigung. Die Summe der Kräfte
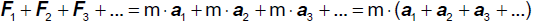
ist dann Null, wenn die resultierende Beschleunigung
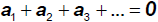
ist. Der Massenpunkt verharrt dann in Ruhe oder gleichförmiger Translation. Wir sagen: "Es herrscht
statisches Gleichgewicht." Ruhe und gleichförmige Bewegung sind offenbar kaum verschiedene Zustände; es sind ihnen alle wesentlichen
Merkmale gemeinsam

Die folgenden Abbildungen demonstrieren an zwei Beispielen das statische Gleichgewicht eines
Massenpunktes.
Im linken Teil der Abbildung besteht Gleichgewicht sowohl in Ruhe als auch bei gleichförmiger Auf- oder
Abwärtsbewegung des Körpers (die Lagerreibung der Rolle sei vernachlässigbar klein). In der Versuchsanordnung rechts stellt sich
bei gegebenem Betrag der Kräfte F1, F2 und
F3 der Punkt P so ein, dass die Summe dieser Kräfte verschwindet.
Jede Kraft kann nun, wie jeder Vektor, auf viele Arten in Teilkräfte (Summanden, Komponenten) zerlegt werden. Je nach Art der gestellten
Aufgabe wählt man eine zweckmäßige Zerlegung. Dazu betrachten wir einige Beispiele.

Das Gewicht G = m·g eines
Körpers auf der schiefen Ebene zerlegen wir zweckmäßig in eine zur schiefen Ebene normale
Komponente D (drückende Komponente) und eine zur Ebene parallele
Komponente T (treibende Komponente).
Der drückenden Komponente wird durch die als starr angenommene schiefe Ebene das Gleichgewicht gehalten.
Um den Körper in Ruhe zu erhalten oder um ihn gleichförmig auf- oder abwärts zu bewegen, muss bei Vernachlässigung der Reibung der
treibenden Komponente durch eine gleich große Gegenkraft das Gleichgewicht gehalten werden. Wirkt eine solche Kraft nicht, so wird der
Körper mit der Kraft

entlang der schiefen Ebene hinabgetrieben und erfährt eine konstante Beschleunigung a.

(Quelle: Icons erstellt von prettycons, https://www.flaticon.com/de/kostenloses-icon/lampe_899369, 17.06.2021) |
 |
Die obige Abbildung (Animation) zeigt eine an einem Stahlseil hängende Straßenbeleuchtung;
das Seil ist links und rechts an Hauswänden in gleicher Höhe verankert. Die beiderseits der Lampe gleich großen Spannkräfte des
Seiles müssen eine zum Lampengewicht G entgegengesetzt gleiche Resultierende ergeben. Die Animation zeigt, dass
die Spannkraft im Seil wesentlich größer sein kann als das Gewicht der Lampe.
Elastische Reaktionskräfte
 |
An einer Schraubenfeder hängt ein Körper der Masse m. Auf ihn wirkt die
Schwerkraft G = m·g. Die Feder wird dadurch gedehnt und reagiert auf diese
Formänderung (Längenzuwachs) durch eine elastische Kraft Fe. Wenn der angehängte
Körper in Ruhe verharrt, hält diese elastische Reaktionskraft (Spannkraft) dem Gewicht des Körpers das Gleichgewicht. Die
Anordnung ist im statischen Gleichgewicht und es gilt
|
|
Um den Zusammenhang zwischen der elastischen Kraft Fe und der
Dehnung Δl der Schraubenfeder festzustellen, belasten wir die Feder mit verschiedenen Gewichtsstücken bekannter Masse und bestimmen
die im statischen Gleichgewicht sich einstellende Dehnung Δl.
Es ergibt sich ein lineares Kraftgesetz, das Hookesche
Gesetz (Robert Hooke 1635 – 1703): Bei nicht zu großer Dehnung ist die Spannkraft der Feder zur Dehnung
proportional. Der Gültigkeitsbereich dieses Gesetzes heißt Proportionalitätsbereich.

Die Konstante k entspricht dem Anstieg der Geraden in der obigen Abbildung und heißt
Federkonstante; ihre kohärente Einheit ist gegeben durch

Die Federkonstante k gibt an, welche Kraft zur Dehnung der Feder um 1 m nötig wäre, wenn
dabei der Proportionalitätsbereich nicht überschritten wird. Da die elastische Kraft der Feder mit der Dehnung in einem umkehrbar
eindeutigen Zusammenhang steht, kann die Feder zur Kraftmessung verwendet werden (Federwaage).

(Quelle: https://www.profishop.at/pesola-zug-kraftmesser-federwaage-50n-teilung-0-5n-macro-linie-braun-mit-haken-80049, 19.06.2021)
Die Federwaage ermöglicht eine statische Kraftmessung. Die Teilstriche haben nach dem Hookeschen Gesetz
gleichen Abstand. Es können Gewichte an jedem Ort gemessen werden; es können aber auch Massen gemessen werden, wenn die Erdbeschleunigung am
Messort bekannt ist.
Die Reibungskraft
Wenn ein Körper (z.B. ein Holzklotz) auf einem anderen (z.B. einem Tisch) gleitet, kommt er
stets zur Ruhe. Die auf einen Körper wirkenden Reibungskraft Fr ist eine Folge der Bewegung. Da die
Reibungskraft die Bewegung stets verzögert, ist sie dem Geschwindigkeitsvektor (der Bewegungsrichtung) stets entgegengesetzt gerichtet. Die
folgenden Versuche zeigen die Eigenschaften der Reibungskraft zwischen festen Körpern.
Ein auf einer Unterlage ruhender Körper kommt erst in Bewegung, wenn die Kraft, mit der wir an der
Federwaage ziehen, einen bestimmten Wert überschreitet (Haftreibung). Um dann den Körper in gleichförmiger Bewegung zu halten,
genügt eine geringere Kraft (Gleitreibung).
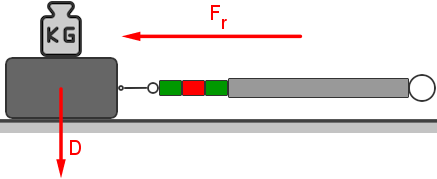
(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)
Der Betrag der Reibungskraft Fr ist zum Betrag der
Belastung D proportional. Die Reibungskraft ist von der belasteten Fläche (fast) unabhängig.

(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)

(Quelle: Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)
Indem wir Körper aus verschiedenen Materialien und mit verschiedener Oberflächenbeschaffenheit
aufeinander gleiten lassen, finden wir eine Abhängigkeit der Reibungskraft von der Oberflächenbeschaffenheit und vom Material der
Körper. Die Reibungskraft hat ihre Ursache in der "Verzahnung", welche die Oberflächenstrukturen bei der Berührung
erfahren.

Oberfläche eines Schleifsteins ("Belgischer Brocken") bei 5000-facher Vergrößerung
(Quelle: "Surface of a Coticule stone, 5000x" by ZEISS Microscopy is licensed with CC BY-NC-ND 2.0,
https://search.creativecommons.org/photos/e5aa7a3d-77cb-4169-a642-1ea50136eeeb, 21.06.2021)
Die Reibungskraft (der Reibungswiderstand) Fr kann
annähernd durch die Formel

dargestellt werden. Die darin enthaltene dimensionslose Größe f ist die sogenannte
Reibungszahl und D die Belastung normal zur Unterlage. Die Reibungszahl f bringt die Abhängigkeit der Reibung von
Material und Oberflächenbeschaffenheit zum Ausdruck. Die folgende Tabelle zeigt einige Haftreibungszahlen fH und
Gleitreibungszahlen fG.

Die Trägheitskraft
Trägheitskräfte, auch Scheinkräfte genannt, treten in beschleunigten Bezugssystemen als real
wirkende Kräfte auf. Sie wirken stets entgegen der Beschleunigung. Betrachten wir dazu das folgende Beispiel.
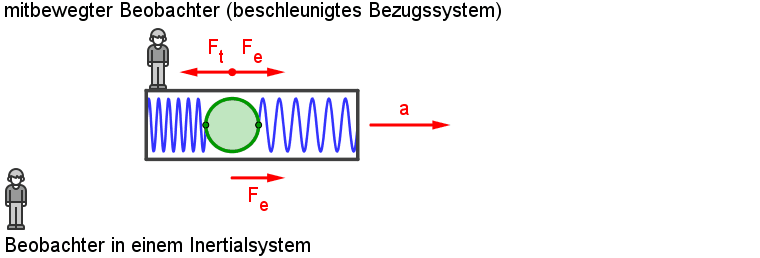
(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020) |
 |
In einem Behälter befindet sich eine Kugel der Masse m. Die Kugel ist mit zwei Federn an den
Seitenwänden des Behälters befestigt. Der Behälter erfährt eine Beschleunigung a gegenüber
einem außenstehenden Beobachter, der sich in einem Inertialsystem befinden möge. Auf die elastisch gehaltene Kugel wird über die Feder
eine Kraft Fe = m·a in Richtung der Beschleunigung ausgeübt.
Für den Beobachter im Inertialsystem ist dies die einzige Kraft, die auf die Kugel wirkt. Aus der Verformung der Feder kann er auf die
Beschleunigung der Kugel bzw. des Behälters schließen. Der Behälter ist also ein Beschleunigungsmesser.
Für einen mit dem Behälter beschleunigt mitbewegten Beobachter stellt sich der Sachverhalt jedoch anders dar. Die Kugel befindet sich aus
seiner Sicht in Ruhe. Soll die dynamische Kraftdefinition allgemein gelten (also in jedem Bezugssystem), so muss die Summe der auf die Kugel
wirkenden Kräfte Null sein. Da aber die verformte Feder anzeigt, dass auf die Kugel eine Kraft Fe
ausgeübt wird, muss auf die Kugel eine weitere Kraft Ft (die Trägheitskraft) wirken, sodass
Fe + Ft = 0
ist. Da die Feder für den mitbewegten Beobachter dieselbe Verformung zeigt wie für den Beobachter im Inertialsystem, muss
Ft = −m·a sein. Dabei bedeutet a
jedoch nicht die Beschleunigung der Kugel (die ist ja in Ruhe), sondern die Beschleunigung des Behälters (also des Bezugssystems) gegen
ein Inertialsystem.
Während alle anderen Kräfte auf einem Körper durch Wechselwirkung mit anderen Körpern verursacht werden und von der Wahl des
Bezugssystems unabhängig sind, ist die Trägheitskraft Ft eine Folge der Beschleunigung gegen ein
Inertialsystem. Es ist für sie keine Wechselwirkung mit anderen Körpern als Ursache ersichtlich, es sei denn, wir betrachten die
Beschleunigung eines Körpers gegen ein Inertialsystem als neue Wechselwirkung. Allgemeingültig können wir sagen:
| |
Die dynamische Kraftdefinition soll in jedem Bezugssystem gelten. Damit dies der Fall
ist (F = 0 für
a = 0), muss in einem mit at gegen ein
Inertialsystem beschleunigten Bezugssystem auf einen Körper der Masse m eine Trägheitskraft
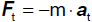
wirken. In einem
Inertialsystem (at = 0) verschwindet die Trägheitskraft. |
|
Betrachten wir nochmals den freien Fall. Von der Erde aus gesehen (die wir hier als Inertialsystem
annehmen wollen) wirkt auf einen frei fallenden Körper nur die Gravitationskraft G. Sie erteilt dem Körper
eine Beschleunigung g, es ist also G = m·g. In
einem mit dem fallenden Körper verbundenen Bezugssystem lautet die Beschreibung anders: Auf den Körper wirkt unverändert die
Gravitationskraft G. Das Bezugssystem ist mit g gegen die Erde beschleunigt; es wirkt daher
eine Trägheitskraft Ft = −m·g, sodass
G + Ft = 0. Ein frei fallender Mensch
spürt von seinem Gewicht nichts, weil dem Gewicht durch die Trägheitskraft das Gleichgewicht gehalten wird; er ist daher
kräftefrei ("schwerelos").
12. Das Gleichgewicht eines starren Körpers
Statisches Gleichgewicht am Hebel (Drehmoment)

Archimedes von Syrakus (um 287 v. Chr. – 212 v. Chr.)
(Quelle: https://commons.wikimedia.org/wiki/File%3AArchimedes1.jpg, 25.06.2021) |
"δός μοι ποῦ στῶ
καὶ κινῶ τὴν γῆν"
"Gib mir einen Punkt, wo ich hintreten kann, und ich bewege die Erde." |
|
Als Hebel bezeichnen wir jeden starren, um eine feste Achse drehbaren Körper. Damit schränken wir
die Bewegungsfreiheit des Körpers auf einen Freiheitsgrad der Rotation ein. Der in der folgenden Abbildung dargestellte Körper soll sich nur
um die feste Achse A drehen können, eine Translation ist ausgeschlossen.
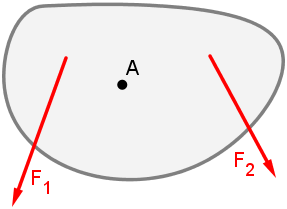
Die Kraft F1 würde den Körper gegen den Uhrzeigersinn um
die Achse A in Drehung versetzen. Soll der Körper in Ruhe bleiben, muss zumindest eine zweite
Kraft F2 so wirken, dass sie eine Drehung im entgegengesetzten Sinn anstrebt. Wir betrachten die drehende
Wirkung der beiden Kräfte als gleich, wenn der ruhende Körper in Ruhe bleibt. Dazu müssen wir die drehende Wirkung einer
Kraft F bezüglich einer gegebenen Achse A definieren.

| |
Ein Maß für die Drehwirkung einer gegebenen Kraft F, deren
Wirkungslinie w in einer zur gegebenen Drehachse A normalen Ebene liegt, ist das Produkt aus dem Betrag der
Kraft F und dem Abstand r der Wirkungslinie w von der Drehachse A. Dieses Maß wird als
Drehmoment M der Kraft F bezüglich der gegebenen Achse A bezeichnet.

|
|
Der Abstand r wird als Kraftarm bezeichnet. Wir werden später sehen, dass das Drehmoment auch als
Vektor dargestellt werden kann. Als kohärente Einheit für das Drehmoment erhalten wir

Das Drehmoment M einer gegebenen Kraft F bezüglich einer gegebenen
Drehachse A ändert sich nicht, wenn die Kraft F entlang ihrer Wirkungslinie w verschoben wird. In der
obigen Abbildung ist die Kraft F in zwei Komponenten Fx und
Fy zerlegt. Die Komponente Fx besitzt keine drehende
Wirkung (ihre Wirkungslinie geht durch die Drehachse). Aus der Ähnlichkeit der durch F und
Fy bzw. durch r und rx gebildeten Dreiecke folgt

F und Fy besitzen daher bezüglich der
Drehachse A die gleiche Drehwirkung. Wir kehren nun zur Frage nach dem statischen Gleichgewicht am Hebel zurück. Dazu verschieben wir die
Kräfte F1 und F2 so entlang ihrer Wirkungslinien, dass ihre
Angriffspunkte und die Drehachse A auf einer Geraden liegen und zerlegen F1 und
F2 jeweils in zwei Komponenten.

Wegen der Gleichheit der Drehmomente von F1 und
F1,y bzw. F2 und F2,y bezüglich
der Drehachse ist der Körper in der folgenden linken Abbildung genau dann im Gleichgewicht, wenn er in der rechten Abbildung im Gleichgewicht
ist.
Wir betrachten die rechte Abbildung und bestimmen die Resultierende der beiden
Kräfte F1,y und F2,y. Geht die Wirkungslinie dieser Resultierenden
durch die Drehachse A, dann befindet sich der Körper im Gleichgewicht.

Da wir die Kräfte F1,y und
F2,y nur entlang ihrer Wirkungslinien verschieben dürfen, können wir sie nicht einfach entsprechend der
Vektoraddition durch Aneinanderhängen addieren. Wir nehmen daher zwei gleich große, entgegengesetzt gerichtete
Hilfskräfte H und −H an (siehe obige Abbildung). Da die Wirkungslinien von
H und −H durch die Drehachse verlaufen, bewirken diese beiden Kräfte keine
zusätzlichen Drehmomente. Wir bilden die Resultierenden R1 und R2,
verschieben diese entlang ihrer Wirkungslinien bis zum Schnittpunkt S und setzen sie mit der Parallelogrammregel zur
Resultierenden R zusammen. R ist die Resultierende von
F1,y und F2,y (H und
−H heben einander auf) und damit zu diesen beiden Kräften parallel. Aus den entstehenden ähnlichen Dreiecken
entnehmen wir: Die Wirkungslinie der Resultierenden R geht genau dann durch die Drehachse A, wenn

bzw.

gilt. Daraus folgt

und damit für die ursprünglich betrachteten
Kräfte F1 und F2

Das ist das Hebelgesetz.
| |
Am Hebel herrscht Gleichgewicht, wenn die Summe der rechtsdrehenden Drehmomente gleich
der Summe der linksdrehenden Drehmomente ist. |
|
Meist dient ein Hebel dazu, mit einer kleineren Kraft (am langen Kraftarm) einer größeren
Kraft (am kurzen Kraftarm) das Gleichgewicht zu halten. Der Hebel ist also ein "Krafttransformator".

Brechstange
Wenn wir nur die Translation eines Körpers betrachten und voraussetzen, dass eine Drehung ausgeschlossen
ist, sind allein Betrag und Richtung der Kraft maßgebend, die Lage der Wirkungslinie ist gleichgültig. Überall, wo es auf Drehungen
ankommt, ist das Drehmoment maßgebend. Da bei technischen Geräten (z.B. Motoren, Schrauben, ...) Drehungen häufig
vorkommen, ist das Drehmoment eine wichtige technische Größe.
Soll eine Schraube in genau vorgeschriebener "Stärke" angezogen werden, so ist anzugeben, mit welchem Drehmoment sie anzuziehen ist, damit sie
zwar möglichst stark, aber nicht bis zur Überlastung angezogen wird.

Ein Automotor entwickelt an der Kurbelwelle ein bestimmtes Drehmoment bei einer bestimmten Zahl von
Umdrehungen pro Minute. Da sich die Räder des Autos langsamer drehen sollen als der Motor, muss die "Drehzahl" n durch ein
Übersetzungsgetriebe vermindert werden.

Übersetzungsgetriebe
Wirkt am angetriebenen kleinen Rad ein Drehmoment M1, so wirkt an seiner Peripherie eine
Kraft
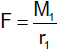
Dieselbe Kraft wirkt an der Peripherie des größeren Rades und erzeugt an diesem Rad ein
Drehmoment

Es gilt daher

Ein Getriebe übersetzt Drehzahlen und Drehmomente. Das Drehmoment wird im umgekehrten Verhältnis
der Drehzahlen übersetzt.
Das Kräftepaar
Wir haben bisher vom Drehmoment einer Kraft gesprochen. Tatsächlich wird aber ein Drehmoment niemals von
einer Einzelkraft ausgeübt.
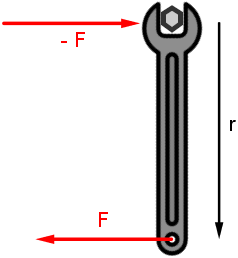 |
Wenn wir z.B. an einem Fahrrad eine Radmutter festziehen wollen und nur eine
Kraft F am Schraubschlüssel angreifen lassen, so wird sich das Rad (sofern wir es nicht festhalten, also
sofern wir keine weitere Kraft angreifen lassen) in Richtung der Kraft F verschieben. Um das zu verhindern, müssen
wir eine zu F entgegengesetzt gleiche Kraft −F angreifen lassen, wir müssen
"dagegenhalten". Die beiden Kräfte haben die
Kraftsumme F + (−F) = 0, sie heben
einander in ihrer verschiebenden Wirkung auf; sie haben aber das Drehmoment F·r (wie F alleine), da der
Kraftarm von −F Null ist. |
|
Ebenso verhält es sich bei dem um eine feste Achse drehbaren Hebel.

Durch die Kräfte F1 und
F2 wird der Körper mit einer
Kraft (F1+F2) gegen die Achse gedrückt, die darauf mit einer
Gegenkraft (−F1−F2) reagieren muss, wenn eine Translation
vermieden werden soll. So wird das Drehmoment M1 = F1·r1 durch das aus
F1 und −F1 gebildete Kräftepaar und das
Drehmoment M2 = F2·r2 durch das aus F2 und
−F2 gebildete Kräftepaar erzeugt. Wir definieren: Zwei entgegengesetzt
gleiche Kräfte F und −F heißen ein Kräftepaar. Es gilt dann:
Jedes Drehmoment wird durch ein Kräftepaar ausgeübt. Nur wenn wir die auftretenden Reaktionskräfte außer Acht lassen, können
wir vom Drehmoment einer Einzelkraft sprechen.
Wir bestimmen nun das Drehmoment eines Kräftepaares bezüglich einer beliebigen (aber zur Ebene
des Kräftepaares normalen) Drehachse.
 |
Drehmoment der Kraft F (rechtsdrehend):

Drehmoment der Kraft −F (linksdrehend):
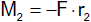
Gesamtdrehmoment des Kräftepaares (rechtsdrehend):

|
|
Das Drehmoment eines Kräftepaares ist von der Lage der Drehachse unabhängig. Ein Kräftepaar
hat bezüglich jeder zur Ebene durch die Wirkungslinien normalen Drehachse das Drehmoment

Dabei ist F der Betrag einer Kraft und d der Abstand der Wirkungslinien. Ein Kräftepaar hat nur drehende
Wirkung; es hat keine verschiebende Wirkung, da die Summe der Kräfte Null ist.
Der Drehmomentvektor
Das Drehmoment eines Kräftepaares hat neben einem Betrag M = F·d auch einen
Drehsinn, ebenso wie eine Kraft neben einem Betrag auch eine Richtung hat. Ebenso wie wir Betrag und Richtung einer Kraft durch einen Pfeil zum
Ausdruck bringen, können wir Betrag und Drehsinn eines Drehmoments durch einen Pfeil darstellen: Das Drehmoment M
eines Kräftepaares F und −F ist ein Vektor, der normal zu der von
F und −F bestimmten Ebene ist. Der Betrag des Vektors ist der Betrag F·d des
Drehmoments; blickt man in Richtung dieses Vektors, so wirkt das Drehmoment im Uhrzeigersinn. Diese Festlegung erfüllt die Eigenschaften des
vektoriellen Produkts.

(Quelle: https://www.gebhardt-stahl.de/lufttechnik/luftkanalaussteifung/schrauben/, 23.05.2021) |
 |
13. Der Schwerpunkt (Massenmittelpunkt)
Die experimentelle Bestimmung des Schwerpunkts
Wir betrachten einen Körper unter der Wirkung der
Schwerkraft (g = konst.). An einem z.B. aus Karton geschnittenen "zweidimensionalen" Körper
lässt sich durch Probieren ein Unterstützungspunkt S finden, sodass der Körper in Ruhe bleibt. Bezüglich jeder durch diesen
Punkt gehenden Drehachse ist der Körper (der ein Hebel ist) unter der Wirkung der Schwerkraft im statischen Gleichgewicht. Für einen
dreidimensionalen Körper lässt sich ebenfalls ein Punkt mit dieser Eigenschaft finden.

Wir nennen diesen so gefundenen Punkt S den Schwerpunkt (Massenmittelpunkt) des Körpers. Jede
Gerade durch den Schwerpunkt heißt Schwerlinie.

Wir denken uns den Körper in kleine Teilchen der
Massen m1, m2, m3, ... zerlegt. Die Summe dieser Massen ist die Gesamtmasse m. Auf jedes
Teilchen wirkt die Schwerkraft: G1 = m1·g,
G2 = m2·g, ... Die Summe dieser Teilkräfte ist
das Gesamtgewicht G = m·g. Jedes dieser Teilgewichte übt auf den um
eine Schwerpunktsachse (Schwerlinie) drehbaren Körper ein Drehmoment aus. Da der Körper im statischen Gleichgewicht ist, muss die Summe
dieser Drehmomente verschwinden. Wenn wir uns die gesamte Masse des Körpers im Schwerpunkt vereinigt denken, so greift auch die gesamte
Schwerkraft m·g dort an. Ihre Wirkungslinie geht in jeder Lage des Körpers durch den Schwerpunkt, das
Drehmoment des Gesamtgewichtes ist bezüglich jeder Schwerpunktsachse Null, da der Kraftarm stets Null ist. Das im Schwerpunkt angreifende
Gesamtgewicht ist also nicht nur die Summe der Teilgewichte, sein Drehmoment bezüglich einer Schwerlinie ist gleich der Drehmomentsumme der
Teilgewichte. Durch die Einführung des Schwerpunktes kann ein ausgedehnter Körper unter Wirkung der Schwerkraft wie ein Massenpunkt
behandelt werden. Damit ergibt sich folgende Möglichkeit zur experimentellen Bestimmung des Schwerpunktes.

Wir hängen den Körper an einem Faden auf; er stellt sich dann in eine bestimmte Ruhelage
ein (statisches Gleichgewicht). Das Lot durch den Aufhängungspunkt (um den der Körper drehbar ist), muss den Schwerpunkt enthalten
und damit eine Schwerlinie sein. Läge der Schwerpunkt S außerhalb dieses Lotes, so würde das Drehmoment des im Schwerpunkt
angreifenden Gesamtgewichtes nicht verschwinden und den Körper in eine andere Lage drehen. Den Schwerpunkt S finden wir nun als Schnittpunkt
zweier Schwerlinien.
Die Berechnung des Schwerpunktes
Wir legen den Körper in ein rechtwinkeliges Koordinatensystem und denken ihn in
Massenpunkte m1, m2, ... zerlegt. Wir suchen die Koordinaten des
Schwerpunktes S ( xS | yS | zS ).

Um die Koordinate xS zu finden, legen wir eine zur z-Achse parallele Drehachse durch den
Schwerpunkt S des Körpers und verlangen, dass die Drehmomentsumme der in den Massenpunkten angreifenden Schwerkraft verschwindet. Die Summe
der Drehmomente ist

Daraus erhalten wir
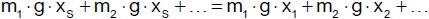
bzw.

Auf der linken Seite steht das mit dem Kraftarm xS multiplizierte Gesamtgewicht des
Körpers, also das Drehmoment des in S angreifenden Gesamtgewichtes bezüglich einer Drehachse durch den Ursprung des Koordinatensystems.
Rechts steht die Summe der Einzeldrehmomente bezüglich derselben Achse. Da der Ursprung beliebig gewählt werden kann, bedeutet das, dass das
Drehmoment des im Schwerpunkt angreifenden Gesamtgewichtes bezüglich jeder Drehachse gleich der Drehmomentsumme der Teilgewichte ist, wenn
g = konst. ist. Aus der letzten Gleichung folgt für die Koordinate xS der
Schwerpunktes S
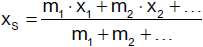
Da keine der drei Koordinatenachsen vor den anderen ausgezeichnet ist, gilt analog

Für den Ortsvektor rS nach dem Schwerpunkt gilt daher

14. Mechanische Arbeit und Energie
Die mechanische Arbeit
Der im Alltag gebräuchliche Begriff "Arbeit" stellt keine messbare Größe dar. So lässt
sich nicht angeben, welches Maß an "geistiger Arbeit" welchem Maß an "körperlichen Arbeit" entspricht. Wir definieren: Mechanische
Arbeit wird verrichtet, wenn ein Körper durch eine Kraft entlang eines Weges bewegt wird.
| |
Unter mechanischer Arbeit W verstehen wir das Produkt aus der
Kraftkomponente Fs in der Wegrichtung und dem zurückgelegten Weg s.

|
|
Die Arbeit ist eine skalare Größe. Als kohärente Einheit erhalten wir im SI

Die obige Definitionsgleichung ist nur anwendbar, wenn die in Wegrichtung wirkende Kraftkomponente konstant
ist. Weist die Kraft F überhaupt in die Wegrichtung, dann gilt

Da in der obigen Abbildung die Kraftkomponente Fs die
Normalprojektion der Kraft F auf den Verschiebungsvektor s darstellt, lässt sich
die Arbeit auch als skalares Produkt schreiben.

Erfolgt die Bewegung eines Körpers normal zu einer Kraft, so verrichtet diese Kraft keine Arbeit, da
ihre Kraftkomponente in der Wegrichtung Null ist. Dieser Fall liegt z.B. vor, wenn ein Körper horizontal verschoben wird. Es wird dann gegen die
Schwerkraft keine Arbeit verrichtet.
Die bisherige Definition der Arbeit ist nur anwendbar, wenn die Kraft konstant ist. Im Kraft-Weg-Diagramm kommt dann die
Arbeit W = F·s als Fläche eines Rechtecks zum Ausdruck.

Ist die Kraftkomponente in der Wegrichtung nicht konstant, so können wir die Arbeit aus dem
Kraft-Weg-Diagramm ermitteln.

Wir zerlegen den zurückgelegten Weg s in kleine Abschnitte Δs und nehmen an, dass die
Kraft innerhalb jedes Wegstücks konstant ist, etwa gleich der Kraft F1 zu Beginn des Wegstücks. Die Summe der Flächen
aller Rechteckstreifen ist ein Näherungswert für die auf dem Weg s verrichtete Arbeit.

bzw. in Vektorschreibweise

In je kleinere Wegstücke wir den Weg unterteilen, desto weniger weichen die als konstant angenommenen
Kräfte innerhalb jedes Wegintervalls von der tatsächlichen Kraft ab. Die "Treppenkurve" nähert sich dann besser der "Kraftkurve", die
Summe der Rechteckflächen nähert sich der Fläche "unter der Kurve". Das führt auf die allgemeine Formel für die mechanische
Arbeit in Form eines Weg- oder Kurvenintegrals.

Darin ist C der im Raum gegebene Weg, den der Angriffspunkt s der
Kraft F(s) von Anfang bis Ende zurücklegt.
Die Speicherung der Arbeit in umkehrbaren Prozessen
Bei vielen Vorgängen wird die mechanische Arbeit "konserviert" und kann durch Umkehr des Vorgangs wieder
zurückerhalten werden.
Heben eines Körpers
 |
Um einen Körper mit dem Gewicht G um die Höhe h
lotrecht zu heben, muss eine Kraft −G entgegen der Richtung der Schwerkraft wirken. Diese Kraft ist nicht nur
imstande, der Schwerkraft am ruhenden Körper das Gleichgewicht zu halten, sie kann den Körper auch in gleichförmiger Bewegung heben, da
der kräftefreie
Körper (G + (−G) = 0) in Bewegung
verharrt, wenn er einmal in Bewegung ist. Um ihn in Bewegung zu setzen, ist nur am Anfang eine geringe zusätzliche Kraft nötig, die wir
vernachlässigen können. Beim Heben eines Körpers um die Höhe h verrichtet man die Hebearbeit

|
|
Lässt man nun den Körper aus der Höhe h herabsinken, dann verrichtet die an ihm
angreifende Schwerkraft G entlang des Weges −h dieselbe Arbeit G·h. Der Körper kann unter
Verlust seiner höheren Lage z.B. einen gleich schweren Körper um die Höhe h heben, also die Arbeit G·h verrichten. In
der folgenden Anordnung genügt der geringste Anstoß, um den Vorgang einzuleiten. Eine während des Vorgangs nötige kleine Kraft
auf Seiten des sinkenden Körpers dient nicht zum Heben, sondern zur Überwindung der unvermeidlichen Reibung.
| Wir definieren: |
 |
| Energie ist die Fähigkeit zur Verrichtung von Arbeit. |
Ein bezüglich eines gegebenen Nullniveaus um die Höhe h gehobener Körper hat die Energie
der Lage (potentielle Energie)

Die Energie der Lage ist eine relative Größe.
Spannen einer Feder
Beim Dehnen einer Schraubenfeder muss entlang des Weges Δl nach dem Hookeschen Gesetz die
Kraft F = k·Δl wirken. Die Kraft ist jetzt nicht konstant.
Die Dehnungsarbeit entspricht der Fläche unter der Kraft-Weg-Geraden.

Beim Entspannen kann die Feder entlang desselben Weges mit einer Kraft vom selben Betrag Arbeit verrichten,
die Dehnungsarbeit kann daher vollständig zurückerhalten werden. Die gespannte Feder besitzt die Energie der (gespannten)
Lage (potentielle Energie)

Beschleunigung eines Körpers
Wird ein Körper der Masse m aus der Ruhe durch eine konstante Kraft F entlang eines
Weges s gleichmäßig beschleunigt, so wird dabei eine Beschleunigungsarbeit

verrichtet. Dabei wird vorausgesetzt, dass keine Reibung auftritt. Bremst man nun den Körper mit einer
Kraft −F ab (sie weist in die entgegengesetzte Richtung von v), so übt der
Körper nach dem Gegenwirkungsgesetz auf die Umgebung (z.B. durch Reibung auf die Unterlage) eine Kraft F aus
und legt bis zum Stillstand einen Weg s zurück. Der Körper verrichtet bis zum Stillstand die Arbeit (vgl. Bremsstrecke eines
Fahrzeugs)

Das bedeutet: Ein mit der Geschwindigkeit v bewegter Körper der Masse m hat die
Bewegungsenergie (kinetische Energie)

Nicht umkehrbare Vorgänge
Ziehen wir einen Körper unter Überwindung der Reibungskraft gleichförmig über eine
horizontale Unterlage, so verrichten wir dabei Arbeit. Der Körper erlangt dabei aber weder größere Höhe (also keine
größere potentielle Energie) noch größere Geschwindigkeit (also keine größere kinetische Energie). Wir wissen
jedoch, dass durch Reibung Wärme entsteht. Wärme ist zwar auch eine Form von Energie, der beschriebene Vorgang ist aber nicht umkehrbar, er
ist irreversibel. Es ist nicht möglich, dass der Körper entlang seiner Bahn zurückgleitet und dabei die vorher durch Reibung
entstandene Wärme wieder in mechanische Energie verwandelt. Die Arbeit wurde bei diesem Vorgang nicht in Form von potentieller oder kinetischer
Energie "konserviert". Wir unterscheiden
| |
Konservative Kräfte wirken bei reversiblen mechanischen Vorgängen; die
verrichtete Arbeit kann durch Umkehr des Vorgangs zurückerhalten werden. |
|
 |
 |
 |
| |
Nichtkonservative Kräfte wirken bei irreversiblen Vorgängen; die verrichtete Arbeit kann
nicht durch Umkehr des Vorgangs zurückerhalten werden. |
|
15. Das Energieprinzip der Mechanik
Die Umwandlung von mechanischer Energie
Wir definieren:
| |
Potentielle und kinetische Energie werden als mechanische Energieformen bezeichnet. Die
Summe aus potentieller und kinetischer Energie heißt mechanische Energie. |
|
Ein fallender Körper verliert an potentieller Energie, seine Bewegungsenergie nimmt ständig zu.
Wenn die gespannte Sehne eines Bogens einen Pfeil abschießt, verliert sie ihre potentielle Energie; der Pfeil gewinnt Bewegungsenergie. Es gibt
Vorgänge, bei denen eine Umwandlung von Energie erfolgt. Die folgenden Beispiele sollen zeigen, dass es sich dabei nur um eine Umwandlung ohne
Änderung der insgesamt vorhandenen mechanischen Energie handelt.
Das Fadenpendel
Bringt man den Pendelkörper der Masse m aus der Ruhelage (h = 0) in die in der
folgenden Abbildung (Animation) ersichtliche Lage ganz links, so gewinnt er potentielle Energie m·g·h. Lässt man den
Pendelkörper los, so schwingt er mit wachsender Geschwindigkeit gegen die Ruhelage.
Er verliert dabei seine potentielle Energie und gewinnt Bewegungsenergie. Wir beobachten, dass der durch
seine Trägheit über die Ruhelage hinausschwingende Pendelkörper genau in der ursprünglichen Höhe h wieder zur Ruhe
kommt.
Das bedeutet: Die Bewegungsenergie m·v2/2 beim Durchgang durch die Ruhelage reicht
aus, um den Pendelkörper wieder in seine Ausgangshöhe zu heben, also um die Arbeit m·g·h zu verrichten; sie hat also den
Wert m·g·h. Die anfangs vorhandene potentielle Energie wurde völlig in Bewegungsenergie verwandelt.
Der freie Fall
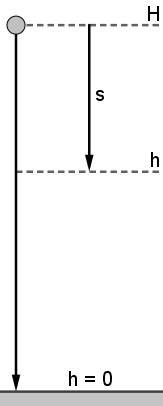 |
Fällt ein Körper der Masse m aus der Anfangshöhe H lotrecht frei herab, so hat er
nach der beliebig gewählten Zeit t den Fallweg

zurückgelegt, also die Höhe

mit einer Geschwindigkeit

erreicht. Seine mechanische Energie ist dann

Die Gesamtenergie des fallenden Körpers ist somit konstant. |
|
Wir verallgemeinern unsere Ergebnisse zum
| |
Energieprinzip der Mechanik: In einem energetisch abgeschlossenen, konservativen
mechanischen System ist die mechanische Energie konstant. Sie kann nicht erzeugt oder vernichtet werden, es kann nur eine Umwandlung der Energieformen
erfolgen. |
|
Ein System heißt energetisch abgeschlossen, wenn ihm von "außen" (also von anderen
Körpern) Energie weder entzogen noch zugeführt werden kann. Es heißt konservativ, wenn in ihm nur konservative Kräfte (also
vor allem keine Reibung) wirksam sind.
Die goldene Regel der Mechanik
"Was man an Kraft spart, muss man an Weg
zusetzen." (Galileo Galilei, 1594)
Mit einfachen Maschinen (Rolle, Hebel, schiefe Ebene, ...) kann man durch Verminderung der Kraft
oder durch Änderung der Kraftrichtung eine Arbeit einfacher verrichten, man kann aber nichts an Arbeit ersparen. Diese sogenannte goldene Regel
der Mechanik ist ein Spezialfall des Energieprinzips der Mechanik, aus dem sie folgt: Könnte eine solche Maschine mehr Arbeit verrichten, als man
ihr zuführt, so könnte man durch wiederholtes Anwenden dieser Maschine mit einer vorhandenen Energie E beliebig viel Arbeit verrichten,
die vorhandene Energie also beliebig vergrößern. Setzt man das Energieprinzip als gültig voraus, so können aus ihm alle
Gesetzmäßigkeiten für einfache Maschinen abgeleitet werden. Wir betrachten dazu einige Beispiele.
Das Wellrad
Ein Wellrad ist eine einfache mechanische Maschine. Es gehört zu den Kraftwandlern. Wellräder
bestehen aus einer Welle (dem Wellbaum) und einem darauf befestigten Rad (dem eigentlichen Wellrad). Mit einem Wellrad lassen sich schwere
Lasten hochheben.

(Quelle: https://commons.wikimedia.org/wiki/File:Innstr._52_
Ziehbrunnen_Blaahaus_Kiefersfelden-1.jpg, 06.07.2021) |

(Quelle: Icons erstellt von Freepik,
https://www.flaticon.com/de/kostenloses-
icon/eimer_517624, 06.07.2021) |
 |
Soll die bei einer Umdrehung am Wellrad verrichtete Arbeit so groß sein, wie die an der Last
verrichtete Hebearbeit, dann muss für eine Umdrehung gelten:
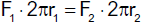
Daraus folgt das Hebelgesetz
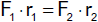
Die schiefe Ebene

(Quelle: Icons erstellt von xnimrodx, https://www.flaticon.com/de/kostenloses-icon/fass_3861027, 07.06.2021)
Wird der Körper mit dem Gewicht G die Strecke h lotrecht gehoben, so
verrichten wir die Arbeit

Zur Berechnung der Arbeit für das Verschieben um die Strecke s entlang der schiefen Ebene zerlegen
wir das Gewicht G des Körpers in eine treibende Komponente F1 und eine
drückende Komponente F2 (vgl. Abschnitt 11). Für die Verschiebearbeit entlang der schiefen
Ebene erhalten wir

Aufgrund ähnlicher Dreiecke gilt

16. Die Leistung
Bei der Definition der Arbeit spielt die Zeit, in der die Arbeit verrichtet wird, keine Rolle. In vielen
Fällen ist es aber wichtig, anzugeben, in welcher Zeit eine bestimmte Arbeit ausgeführt wird. Wenn mit einem Aufzug 1000 Ziegelsteine
auf eine hoch gelegene Baustelle transportiert werden sollen, so kann dies auf verschiedene Weise geschehen: 20 Fahrten mit je 50 Steinen
oder 10 Fahrten mit je 100 Steinen oder ...
In allen Fällen ist die verrichtete Arbeit gleich groß, denn es werden stets 1000 Steine auf die gleiche Höhe gebracht. Trotzdem
besteht zwischen den verschiedenen Tätigkeiten ein Unterschied, weil die gleiche Arbeit in verschiedenen Zeiten verrichtet wird (die
Fahrgeschwindigkeit des Aufzugs wird als konstant angenommen).
Dieser Sachverhalt wird durch eine physikalische Größe, die wir als Leistung (Formelzeichen P) bezeichnen, erfasst. Wir
definieren:
| |
Unter der Leistung P verstehen wir den Quotienten aus der verrichteten Arbeit W
und der benötigten Zeit t.
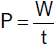
|
|
Für die kohärente Einheit der Leistung ergibt sich im SI:
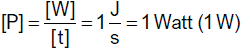
Eine gebräuchliche inkohärente Einheit der Leistung ist die Pferdestärke (PS). Sie ist
als die Leistung definiert, die auf der Erde zum Heben einer Masse von 75 Kilogramm innerhalb eines Zeitraumes von einer Sekunde um eine
Höhe von einem Meter nötig ist.
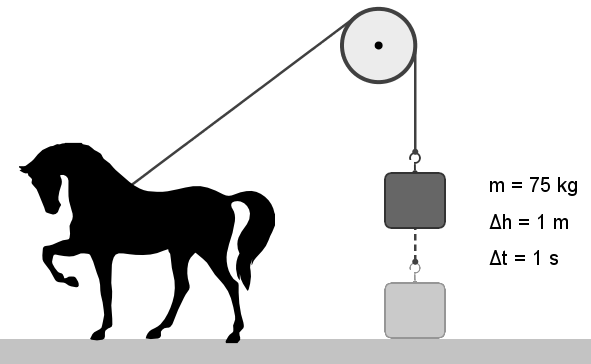
(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/pferd-stehend-auf-drei-pfoten-schwarze-form-der-seitenansicht_35922,
08.06.2021)

Die Arbeit kann auch in der Form

ausgedrückt werden. Für die Einheit der Arbeit schreibt man daher oft
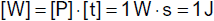
Als größere (inkohärente) Einheit wird vielfach 1 Kilowattstunde (1 kWh)
verwendet.

17. Die Erhaltung der Bewegungsgröße (Impulssatz)
Für ein aus zwei Körpern mit den Massen m1 und m2 bestehendes
abgeschlossenes System gilt bei einer Wechselwirkung (vgl. Abschnitt 9):

Bezeichnen wir mit v1 bzw. v2 die
Geschwindigkeiten der beiden Körper vor der Wechselwirkung und mit v1' bzw.
v2' die Geschwindigkeiten nach der Wechselwirkung, so lässt sich obige Gleichung auch so schreiben:
 |
oder |
 |
Die obige rechte Gleichung besagt, dass die für zwei Körper eines abgeschlossenen Systems gebildete
Summe der Größe m·v vor und nach einer Wechselwirkung denselben Wert hat. Das gilt auch dann, wenn
das System aus beliebig vielen Körpern besteht. Es können nämlich alle auftretenden Wechselwirkungen aus Wechselwirkungen zwischen je
zwei Körpern zusammengesetzt werden.
Für das Produkt m·v gilt offenbar in einem abgeschlossenen System ein Erhaltungssatz. Es wird daher als
eine wichtige physikalische Größe definiert.
| |
Das Produkt aus Masse und Geschwindigkeit eines Körpers wird als seine
Bewegungsgröße (Impuls) p bezeichnet.
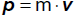
In einem gegen Wechselwirkung mit anderen Körpern abgeschlossenen System bleibt der
Gesamtimpuls (die Summe der Bewegungsgrößen) konstant.

|
|
Wir bezeichnen diesen Erhaltungssatz als Impulssatz. Als kohärente Einheit für die
Bewegungsgröße ergibt sich

Der Impulsbegriff wurde von Isaac Newton eingeführt: Er schreibt dazu in seiner Philosophiae naturalis
principia mathematica: "Quantitas motus est mensura ejusdem orta ex velocitate et quantitate materiae
conjunctim." (Die Größe der Bewegung wird durch die Geschwindigkeit und die Größe der Materie vereint gemessen.)
Die Bewegungsgröße eines Körpers wird dadurch geändert, dass auf ihn während einer
gewissen Zeit eine Kraft einwirkt. Ist die Kraft F im Zeitintervall Δt konstant, so wird der Körper
gleichmäßig beschleunigt (Δv = a·Δt) und es
gilt (für m = konst.)

Die Impulsänderung eines Körpers kann für F = konst. daher
stets in der Form

geschrieben werden. Das Produkt aus Kraft und Zeit heißt Kraftstoß. Die Impulsänderung ist
gleich dem Kraftstoß. In der folgenden Animation erfährt der reibungsfrei bewegliche Wagen durch den Pendelschlag einen Kraftstoß und
damit eine Änderung seines Impulses.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021) |
 |
Die folgende Abbildung zeigt das Kraft-Zeit-Diagramm für eine konstante Kraft.

Dem Kraftstoß entspricht in diesem Diagramm die Fläche eines Rechtecks. Nach den bei der
mechanischen Arbeit angestellten Überlegungen ist leicht einzusehen, dass für eine nicht konstante Kraft ebenso die Fläche unter der
Kraft-Zeit-Kurve dem Kraftstoß entspricht.
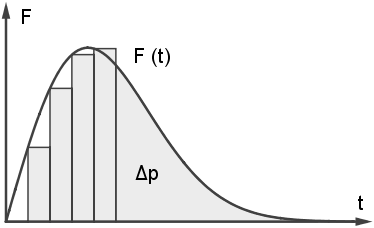
Die Gleichung

kann auch in der Form
 |
oder |
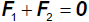 |
geschrieben werden. In dieser Form sagt der Impulssatz, dass die Körper bei jeder Wechselwirkung
entgegengesetzt gleiche Kraftstöße erhalten, deren Summe stets Null sein muss. Der Impulssatz und das Gegenwirkungsgesetz folgen
unmittelbar auseinander, sie sind nur verschiedene Formulierungen ein und desselben Sachverhaltes. Zusammenfassend ergeben sich für den
Impulssatz die folgenden Formulierungen.

18. Anwendungsbeispiele zum Energieprinzip und Impulssatz
Der unelastische Stoß

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Wir betrachten zwei Wagen auf einer waagrechten geraden Schiene. Am ersten Wagen ist eine Nadel angebracht,
am zweiten ein Kork. Die beiden Wagen bewegen sich anfangs mit den Geschwindigkeiten v1 bzw.
v2. Stößt der erste Wagen "zentral" auf den zweiten, so bohrt sich die Nadel so lange in den Kork, bis
die beiden Wagen die gleiche Geschwindigkeit v' erreicht haben. Die "Deformation" am Kork wird nicht mehr
zurückgebildet, die Wagen stoßen einander nicht wieder ab. Die zur Deformation nötige Arbeit wird auf Kosten der Bewegungsenergie
verrichtet. Da die Deformationsarbeit nicht wieder zurückgewonnen wird, ergibt sich ein Verlust an mechanischer Energie. Das System ist nicht
konservativ. Wenn die beiden Wagen frei beweglich sind, ist das System abgeschlossen, und es gilt der Impulssatz (da alle
Geschwindigkeitsvektoren in derselben Geraden liegen, können wir sie durch reelle Zahlen darstellen).

Mit v1' = v2' = v' (gleiche Geschwindigkeiten nach dem
Stoß) erhalten wir

und somit

Der elastische Stoß

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Wir betrachten wieder zwei Wagen, die sich auf einer waagrechten geraden Schiene mit den
Geschwindigkeiten v1 bzw. v2 bewegen. Am ersten Wagen ist eine
Blattfeder angebracht. Diese wird beim Stoß verformt, so lange, bis die beiden Wagen gleiche Geschwindigkeit haben. Dabei wird ein Teil der
Bewegungsenergie in potentielle Energie der elastischen Verformung der Feder umgewandelt. Die beiden Wagen stoßen einander dann wieder ab,
bewegen sich also nach dem Stoß mit ungleichen Geschwindigkeiten v1' bzw.
v2' weiter; die potentielle Energie wird unter Rückbildung der Verformung der Feder in kinetische Energie
zurückverwandelt. Die beiden Wagen bilden ein konservatives, abgeschlossenes System. Es gilt daher der Impulssatz

und das Energieprinzip (die potentielle Energie ist vor und nach dem Stoß Null)

Aus diesen beiden Gleichungen folgt

Division dieser Gleichungen ergibt
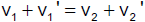
Damit erhalten wir das folgende lineare Gleichungssystem für die Variablen v1' und
v2'

mit den Lösungen

Wir betrachten dazu zwei Spezialfälle.
1. Ein ruhender Wagen wird von einem Wagen gleicher Masse gestoßen.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Aus m1 = m2 = m, v1 ≠ 0 und
v2 = 0 folgt

Der stoßende Wagen kommt völlig zur Ruhe, der gestoßene übernimmt seine
Geschwindigkeit. Die gesamte Energie und der gesamte Impuls des einen Wagens werden auf den anderen übertragen.
2. Ein Wagen stößt normal gegen eine starre ruhende Wand.

(Quelle: Icons erstellt von photo3idea_studio, https://www.flaticon.com/de/kostenloses-icon/wagen_1254280, 23.05.2021
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021) |
 |
Ein starrer Körper soll sich unter der Einwirkung von Kräften nicht verformen. Wir haben daher
v2 = v2' = 0 zu setzen und erhalten aus der zweiten Gleichung des linearen Gleichungssystems
v1' = −v1. Der Wagen prallt also mit umgekehrter Geschwindigkeit von der Wand zurück. Er behält seine
gesamte kinetische Energie, es wird keine Energie auf die Wand übertragen. Wohl wird aber auf die Wand Impuls übertragen:
| |
Impuls des Wagens vor dem Stoß |
 |
 |
 |
 |
| |
Impuls des Wagens nach dem Stoß |
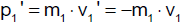 |
 |
 |
 |
| |
Änderung des Impulses |
 |
Die Wand muss den entgegengesetzten Impuls
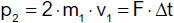
erhalten, da die Summe der Kraftstöße Null sein muss. Dass die Wand trotz des auf sie
übertragenen Impulses in Ruhe bleibt, liegt daran, dass ihr in Berücksichtigung ihrer Starrheit eine unendlich große Masse zugeordnet
werden muss. Ihre Geschwindigkeitsänderung ist daher verschwindend klein.
Das Kugelstoßpendel
Ein Kugelstoßpendel, auch Newtonpendel oder Newton-Wiege genannt, ist eine Anordnung von identischen
elastischen Kugeln (meist aus Metall), die je an zwei (bifilar) gleichen Fäden in einer Reihe aufgehängt sind. Jede Kugel bildet
ein Pendel gleicher Masse und Pendellänge. Der Abstand der Aufhängepunkte ist gleich dem Durchmesser der Kugeln, sodass diese in Ruhe
senkrecht hängen und sich gerade berühren.

(Quelle: https://stock.adobe.com/de/search/images?k=kugelstosspendel&asset_id=50342873, 25.07.2021)
Wenn eine der äußeren Kugeln seitlich mit gestreckten Fäden abgehoben wird und gegen die
Reihe der anderen Kugeln zurückfällt, bewirkt der Anprall, dass genau eine Kugel gegenüberliegend abgestoßen wird, während
die anderen Kugeln in Ruhe bleiben. Pendelt diese Kugel zurück und prallt auf, wird durch den Stoß wieder die äußerste Kugel auf
der anderen Seite abgestoßen.
Bemerkenswert ist das Verhalten bei mehr als einer bewegten Kugel. Wenn zwei oder mehrere Kugeln an die
verbleibenden Kugeln prallen, werden auf der anderen Seite immer ebenso viele Kugeln abgestoßen, wie auf der Gegenseite aufgeprallt sind - und
nicht etwa nur eine einzelne Kugel mit höherer Geschwindigkeit.
Das Verhalten der Kugeln ergibt sich aus der Impulserhaltung in Kombination mit der Erhaltung der
Bewegungsenergie. Nehmen wir an, dass auf der linken Seite k1 Kugel mit der Geschwindigkeit v1 aufprallen und auf der
rechten Seite k2 Kugeln mit der Geschwindigkeit v2 abgestoßen werden. Dann folgt aus der Impulserhaltung

und aus der Energieerhaltung

Die zweite Gleichung kann in der Form

geschrieben werden. Durch Einsetzen ergibt sich

und
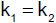
Es fliegen also so viele Kugeln weg wie auftreffen.
Nichtzentraler elastischer Stoß zweier Kugeln
Wir betrachten den Spezialfall des nichtzentralen elastischen Stoßes zweier identischer
Kugeln (Masse m, Radius r), wobei eine Kugel vor dem Stoß ruht. Die beiden Kugeln sollen sich dabei in einer waagrecht liegenden
Ebene bewegen.
Aus den Erhaltungssätzen folgt für den Impuls

und die Bewegungsenergie
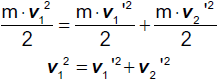
Die Geschwindigkeitsvektoren der beiden Kugeln nach dem Stoß schließen daher aufgrund des
pythagoräischen Lehrsatzes einen rechten Winkel ein.

Damit lassen sich die Geschwindigkeiten der Kugeln nach dem Stoß ermitteln, wenn der
Winkel α2 bekannt ist. α2 hängt von den Bedingungen beim Stoß ab und ergibt sich aus der Neigung der
Verbindungslinie der Schwerpunkte beider Kugeln zur Impulsrichtung p1. Es gilt (vgl. obige
Abbildung)
Daraus folgt für die Geschwindigkeiten nach dem Stoß
Die Raketengrundgleichung von Ziolkowski

Konstantin Eduardowitsch Ziolkowski (1857 – 1935)
(Quelle: https://de.m.wikipedia.org/wiki/Datei:Tsiolkovsky.jpg, 25.07.2021)
Der Raketenantrieb
Der Raketenantrieb macht vom Impulserhaltungssatz Gebrauch. Ein Körper, der einen Teil seiner Masse in
einer Richtung ausstößt, erfährt selbst eine Beschleunigung in der entgegengesetzten Richtung.
Dieses "Rückstoßprinzip" kann aufgrund des Impulserhaltungssatzes folgendermaßen
präzisiert werden. Die von der Rakete erzeugten, unter hohem Druck stehenden Gasmassen werden ausgestoßen und erhalten dabei den
Impuls pGas. Wenn keine äußeren Kräfte wirksam sind, so muss die Rakete dann einen Impuls pRakete
erhalten, der den gleichen Betrag und die entgegengesetzte Richtung wie pGas hat.

Die Raketenformel
Im Folgenden soll die Bewegung einer Rakete genauer untersucht werden, wobei insbesondere auch die vom
russischen Physiker Ziolkowski zuerst angegebene Raketenformel entwickelt wird. Es muss dabei beachtet werden, dass die Raketenbewegung sich von
anderen Bewegungen in einem wesentlichen Punkt unterscheidet. Während die Masse eines Körpers bei anderen Bewegungen im Wesentlichen
unverändert bleibt, ist dies bei der Raketenbewegung nicht der Fall; wegen des Verbrauchs an Treibstoff wird die Masse der Rakete während
des Flugs geringer. Der Treibstoffverbrauch ist dabei so hoch, dass die Massenabnahme keinesfalls vernachlässigt werden darf. Bei den folgenden
Überlegungen werden möglichst einfache Bedingungen vorausgesetzt.
| • |
|
Auf die Rakete wirken keine äußeren Kräfte, d.h. wir sehen vom Luftwiderstand
und von jeder Gravitation ab. |
| • |
|
Die Rakete startet aus der Ruhelage, d.h. zum Zeitpunkt t = 0 soll ihre
Geschwindigkeit v0 = 0 sein. |
Die Start- oder Anfangsmasse sei m0. Diese setzt sich aus zwei Teilen zusammen, nämlich aus
der Masse des Treibstoffs mTr und der gesamten übrigen Masse mL, die den Raketenkörper und die Nutzlast
umfasst. Man bezeichnet diese Masse mL auch als die Leermasse; es ist die Masse, die übrig bleibt, wenn der gesamte Treibstoff
verbraucht ist. Daher gilt

Wir setzen weiter voraus, dass die Rakete während des ganzen Fluges in jeweils gleichen
Zeitintervallen Δt stets die gleiche Gasmasse Δm ausstößt. Die konstante Größe

wird als der Durchsatz oder die Abbrandgeschwindigkeit der Rakete bezeichnet. Die Zeit vom Start bis zum
Brennschluss, d.h. bis zum Verbrauch des gesamten Treibstoffs, bezeichnet man als Brenndauer T. Für die Abbrandgeschwindigkeit gilt dann

Für die Masse mt einer Rakete zu einem beliebigen Zeitpunkt t erhalten wir
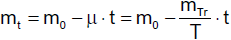
Die Geschwindigkeit der Rakete relativ zur Erde zum Zeitpunkt t sei vt. In dem nun folgenden
Zeitintervall Δt stößt die Rakete die Gasmasse μ·Δt aus. Diese soll relativ zur Rakete die
Ausströmgeschwindigkeit w haben. Durch den Gasausstoß erfährt die Rakete eine Geschwindigkeitszunahme Δv. Am Ende des
betrachteten Zeitintervalls Δt beträgt also
| die Masse der Rakete |
|
 |
| die Geschwindigkeit der Rakete |
|
 |
| und die Geschwindigkeit der Gasmasse relativ zur Erde |
|
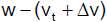 |

Dann gelten für die Impulse der Rakete und der Gasmasse am Ende des Zeitintervalls Δt

Nach dem Impulserhaltungssatz muss die Summe von pRakete und pGas gleich dem Impuls zu
Beginn des betrachteten Zeitintervalls Δt sein, d.h. gleich dem Impuls

Es gilt also

Hieraus folgt weiter

bzw.

Da der Ausdruck

die Beschleunigung der Rakete darstellt, ist

bzw.
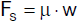
die Kraft, die die Rakete beschleunigt. Man bezeichnet sie als den Vortrieb oder den Schub der Rakete. Es
handelt sich hierbei um eine für jedes Raketentriebwerk charakteristische Größe. Da die Abbrandgeschwindigkeit μ und die
Ausstoßgeschwindigkeit w für ein bestimmtes Raketentriebwerk konstant sind, stellt auch der Schub eine konstante Eigenschaft einer
Rakete dar. Die Beschleunigung, die der Rakete durch den Schub erteilt wird, ist dagegen nicht konstant, sondern sie nimmt mit abnehmender
Raketenmasse zu und erreicht bei Brennschluss den größten Wert.
Statisches Gleichgewicht von Systemen
Ein System besteht aus mehreren Körpern. Dabei sind der Lage und der Bewegung dieser Teile oft gewisse
Bedingungen auferlegt.

In der obigen Abbildung bildet eine Kugel mit einer Schale und der Erde, deren Anziehungskraft sie
unterworfen ist, ein System. Die Kugel soll in der Schale aufliegen, ihre Bewegungsmöglichkeiten werden also durch die Schale eingeschränkt.
Am tiefsten Punkt hat die Kugel gegenüber jeder anderen zulässigen Lage die geringste potentielle Energie. Mit jeder Veränderung dieser
Lage ist eine Erhöhung der potentiellen Energie verbunden, da der Schwerpunkt gehoben werden muss. Dazu ist Arbeit nötig; die im tiefsten
Punkt der Schale liegende Kugel kann daher nie von selbst, also ohne, dass von außen Energie zugeführt wird, ihre Lage verlassen. Wir
sagen: "Das System ist im stabilen Gleichgewicht."
Bringen wir die Kugel aus ihrer stabilen Gleichgewichtslage, so wird sie durch die treibende Komponente der Schwerkraft wieder dorthin
zurückgezogen. Sie kann jetzt, losgelassen, von selbst in die stabile Gleichgewichtslage zurückkehren, da dies mit einer Verminderung der
potentiellen Energie verbunden ist, die in Bewegungsenergie verwandelt wird und somit eine selbstständige Ortsveränderung
ermöglicht.
In der folgenden Abbildung hat die potentielle Energie der Kugel ein Maximum; sie ist größer als
in jeder benachbarten zulässigen Lage.
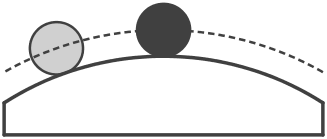
Die auf die Kugel wirkende Schwerkraft hat keine horizontale, also keine treibende Komponente. Die Kugel kann
sich aus dieser Lage nicht von selbst entfernen, das System ist auch in dieser Lage im statischen Gleichgewicht. Nach einer geringen
Ortsveränderung kommt aber die Kugel stets in eine Lage geringerer potentieller Energie und kann daher von selbst nicht wieder in den
Gleichgewichtszustand zurückgelangen, sie bewegt sich vielmehr von selbst im Sinne einer weiteren Verminderung ihrer potentiellen Energie. Wir
nennen diesen Gleichgewichtszustand daher ein labiles Gleichgewicht.

Bei der auf einer horizontalen Ebene ruhenden Kugel führt keine zulässige Lageänderung zu
einer Änderung der potentiellen Energie. Keine solche Lageänderung macht daher potentielle Energie frei, die in Bewegungsenergie verwandelt
werden und so zu einer selbständigen Änderung der Lage des Systems führen könnte. Diesen Zustand bezeichnen wir als
indifferentes Gleichgewicht.
19. Die Erhaltung des Massenmittelpunktes
In einem früheren Abschnitt haben wir für ein System von
Massenpunkten m1, m2, ... mit den
Ortsvektoren r1, r2, ... einen
Massenmittelpunkt (Schwerpunkt) rS definiert.

Ändern nun die Massenpunkte m1, m2, ... innerhalb eines
Zeitintervalls Δt ihre Orte um
Δr1, Δr2, ..., so wird sich auch der Massenmittelpunkt
in dieser Zeit um ein Stück ΔrS verschieben.

Dividieren wir diese Gleichung durch die zur Verschiebung benötigte Zeit Δt, so erhalten wir
für die mittlere Geschwindigkeit des Massenmittelpunktes

Für Δt → 0 streben alle mittleren Geschwindigkeiten gegen die
Momentangeschwindigkeiten. Die Geschwindigkeit des Massenmittelpunktes ist daher gegeben durch

Für den Gesamtimpuls des Systems können wir daher
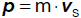
schreiben. Ist nun das System im Sinne des Impulssatzes abgeschlossen, wirken also keine äußeren
Kräfte ein, so ist die in der letzten Gleichung auftretende Bewegungsgröße p konstant. Es ist dann auch
die Geschwindigkeit vS des Schwerpunktes konstant. Insbesondere bewegt sich der Schwerpunkt dieses Systems
bezüglich eines Inertialsystems gleichförmig. Ist der Massenmittelpunkt eines abgeschlossenen Systems zu irgendeinem Zeitpunkt in Ruhe, so
bleibt er ständig in Ruhe. Der Gesamtimpuls eines Systems lässt sich stets als Produkt der Gesamtmasse und der Geschwindigkeit des
Massenmittelpunkts darstellen. Durch innere Kräfte kann die Bewegung des Massenmittelpunktes eines Systems nicht beeinflusst werden.
20. Drehbewegungen
Bei der Translationsbewegung haben wir uns auf die Beschreibung der Bewegung eines Massenpunktes
beschränkt. Da alle Massenpunkte, in die wir uns einen Körper zerlegt denken können, bei einer Translation kongruente Bahnen
durchlaufen, wird durch die Beschreibung der Bewegung eines Massenpunktes die Bewegung des gesamten Körpers beschrieben.
Die Beschreibung der Drehbewegung
Bei der Rotation eines starren Körpers um eine feste Achse beschreiben die einzelnen Massenpunkte
verschiedene Bahnen. Es ist daher zur Beschreibung der Drehbewegung notwendig, neue Größen zu definieren, die für die Bewegung des
Gesamtkörpers charakteristisch sind. Wir beschränken uns vorerst auf die Rotation eines starren Körpers um eine feste Achse A.
Der Phasenwinkel (Drehwinkel) φ
Wir geben die Lage jedes Massenpunktes durch einen Radiusvektor r
an (r1, r2 in der obigen Animation). Er weist zum entsprechenden
Massenpunkt und soll auf die Drehachse A normal stehen. Während einer Zeit t legen verschiedene Punkte des Körpers Bögen
verschiedener Länge zurück (b1, b2). Das Verhältnis b/r ist jedoch für alle Punkte
gleich (b1/r1 = b2/r2), es ist daher für die Gesamtdrehung des Körpers
charakteristisch. Dieses Verhältnis ist geeignet, die Gesamtdrehung des Körpers anzugeben. Wir messen die Drehung eines Körpers durch
den Phasenwinkel (Drehwinkel) φ.
Als kohärente Einheit des Winkels erhalten wir

Die Einheit des Winkels ist als Quotient zweier Längen eine reine Zahl.
Die Winkelgeschwindigkeit ω
Ein Körper rotiert gleichmäßig, wenn die Änderung des Phasenwinkels Δφ
zur dafür benötigten Zeit Δt proportional ist und die Richtung der Drehachse A unverändert bleibt
Der Quotient aus Phasenwinkel und Zeit ist der Betrag der Winkelgeschwindigkeit ω.

Die Winkelgeschwindigkeit einer beliebigen Rotation definieren wir wieder als Grenzwert der mittleren
Winkelgeschwindigkeit für ein gegen Null strebendes Zeitintervall.

Als kohärente Einheit der Winkelgeschwindigkeit erhalten wir

 |
Zur vollständigen Angabe des Rotationszustandes eines Körpers müssen neben dem
Betrag der Winkelgeschwindigkeit noch die Lage der Drehachse und der Drehsinn festgelegt werden. Das geschieht durch die Darstellung der
Winkelgeschwindigkeit als Vektor.
Die Winkelgeschwindigkeit ist eine Vektor ω, der in der Drehachse liegt und dessen Länge gleich dem
Betrag ω der Winkelgeschwindigkeit ist. Die Richtung des Vektors gibt den Drehsinn gemäß der Rechtsschraubenregel an: Dreht man
eine Rechtsschraube mit dem Körper mit, so verschiebt sie sich in Richtung des
Winkelgeschwindigkeitsvektors ω. |
|
Frequenz, Kreisfrequenz und Umlaufzeit (Periodendauer)
Bei einem gleichmäßig rotierenden Körper wiederholt sich ein bestimmter
Bewegungsablauf (1 Umdrehung) immer wieder. Wir nennen solche Vorgänge periodische Vorgänge oder Schwingungen. Die
gleichmäßige Drehbewegung wird daher auch als zirkular polarisierte Schwingung bezeichnet. Die Zeitdauer einer
Umdrehung (einer Periode) heißt Umlaufzeit (Periodendauer) T. Wir definieren:
| |
Unter der Frequenz f eines periodischen Vorgangs verstehen wir die Zahl der Perioden je
Sekunde |
|
Die Einheit der Frequenz ist 1 Periode je Sekunde (1 s−1) und
heißt 1 Hertz (1 Hz). Es gilt
und
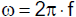
Die Winkelgeschwindigkeit ist also das 2π-fache der Frequenz und wird daher auch als Kreisfrequenz
bezeichnet.
Die Tangentialgeschwindigkeit v
Die Tangentialgeschwindigkeit ist die Bahngeschwindigkeit eines Massenpunktes des rotierenden
Körpers.
Sie besitzt die Richtung der Tangente an die Kreisbahn und hat für eine gleichmäßige Drehung
den Betrag

Der Betrag der Tangentialgeschwindigkeit v entspricht der Fläche des von
ω und r aufgespannten Rechtecks (r und
ω stehen aufeinander normal). Da v sowohl zu ω als auch zu
r normal ist, lässt sich die Tangentialgeschwindigkeit auch als vektorielles Produkt des
Winkelgeschwindigkeitsvektors ω und des Radiusvektors r schreiben. Es gilt

Die Tangentialgeschwindigkeit ist für Punkte mit verschiedenem Betrag des Radiusvektors verschieden; sie
ist nicht wie die Winkelgeschwindigkeit für die Drehung des Gesamtkörpers charakteristisch.
Die Zentripetalkraft
Jeder Massenpunkt eines gleichmäßig rotierenden Körpers bewegt sich für einen nicht
mitrotierenden Beobachter ungleichförmig, da sich die Richtung seiner Geschwindigkeit (Tangentialgeschwindigkeit) ständig ändert.
Jeder Massenpunkt ist daher ständig beschleunigt, und es muss auf ihn ständig eine Kraft wirken, die ihn in die Kreisbahn zwingt. Sobald
diese Kraft aufhört zu wirken, bewegt sich der Massenpunkt (in einem Inertialsystem nach dem Beharrungsgesetz) tangential weiter.

Funken am Winkelschleifer
(Quelle: https://www.heimwerkertricks.net/tipps-tricks/sicherheit/flexen-15-sicherheitsvorschriften-
fuer-die-arbeit-mit-dem-winkelschleifer/ © Ramona Heim - Fotolia.com, 30.07.2021)
Um für einen Massenpunkt des rotierenden Körpers die Beschleunigung zu finden, müssen wir die
Änderung seiner Geschwindigkeit in einer Folge gleicher Zeitintervalle betrachten. Dazu zerlegen wir die Bahnkurve in kleine Abschnitte, die in
gleichen Zeitintervallen Δt zurückgelegt werden. Die folgende Abbildung zeigt die Bewegung eines Massenpunktes in einem solchen
Zeitintervall.

Für die Länge der entstehenden Sehne gilt annähernd

Im rechten Teil der obigen Abbildung sind die Geschwindigkeitsvektoren von einem Punkt M aus
abgetragen (Hodograph). Die Geschwindigkeitsänderung Δv im Zeitintervall Δt verbindet die
beiden Pfeilspitzen. Für die mittlere Beschleunigung im Zeitintervall Δt gilt

Aus der Ähnlichkeit der
Dreiecke A, r1, r2 und
M, v1, v2 folgt

bzw.

Daher gilt für die mittlere Beschleunigung
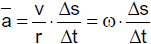
Für ein gegen Null strebendes Zeitintervall strebt die mittlere Beschleunigung gegen die
Momentanbeschleunigung und die Sehne Δs fällt mit dem Bogen Δb zusammen. Es strebt dann Δs/Δt gegen v. Somit
erhalten wir für den Betrag der Momentanbeschleunigung a

Mit Δt → 0 wird zudem Δv zu v
normal. Der Beschleunigungsvektor a ist daher zum Momentangeschwindigkeit v stets
normal, er weist zum Zentrum (Drehachse) hin, wir nennen die Beschleunigung daher
Zentripetalbeschleunigung az. Sie bewirkt keine Änderung des Betrages der Tangentialgeschwindigkeit,
sie ändert nur ihre Richtung. Zusammenfassend lässt sich sagen:
Ein in einer Kreisbahn bewegter Massenpunkt der Masse m erfährt normal zur Bahnkurve eine
Zentripetalbeschleunigung mit dem Betrag
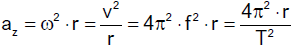
bzw. mit der Vektordarstellung

Das erfordert in einem Inertialsystem eine Zentripetalkraft mit dem Betrag

bzw. mit der Vektordarstellung

Da die Zentripetalkraft zur Wegrichtung stets normal ist, verrichtet sie keine Arbeit und verursacht keine
Änderung des Betrages der Geschwindigkeit.
In der folgenden Animation befindet sich auf einer drehbaren Scheibe ein Behälter mit einer Kugel der Masse m. Die Kugel ist mit zwei Federn
an den
Seitenwänden des Behälters befestigt. Wird die Scheibe in Rotation versetzt, so wird auf die elastisch gehaltene Kugel über die Feder
die Zentripetalkraft Fz = m·az ausgeübt. Für
einen nicht mitrotierenden Beobachter in einem Inertialsystem ist dies die einzige Kraft, die auf die Kugel wirkt.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020) |
 |
Für einen mit der Scheibe mitrotierenden Beobachter gilt jedoch eine andere Beschreibung. Auch er sieht
an der Dehnung der Feder das Wirken der Zentripetalkraft. Für ihn ist jedoch die Kugel in Ruhe. Es wirkt daher auf die Kugel eine vom Zentrum
wegweisende Trägheitskraft Ft, die sogenannte Fliehkraft oder Zentrifugalkraft

Sie ist eine Folge der
Beschleunigung (Zentripetalbeschleunigung az) des Bezugssystems gegen ein Inertialsystem. Von einer auf
einen rotierenden Körper wirkenden Fliehkraft kann daher nur bei Verwendung eines mitrotierenden Bezugssystems gesprochen werden.

(Quelle: Icons erstellt von surang, https://www.flaticon.com/de/kostenloses-icon/abstand-halten_2834333, 01.09.2020) |
 |
Zentrifugen
Zentrifugen sind Behälter, die in schnelle Rotation versetzt werden können. Sie dienen meist zur
Trennung von Stoffen verschiedener Dichte. Für einen mitrotierenden Beobachter gilt: Auf die dichteren Teile (größere Masse)
wirkt größere Fliehkraft, sie werden stärker nach außen getrieben. Der Vergleich der Formeln für die
Schwerkraft (Gewicht)

und die Fliehkraft

zeigt, dass die Fliehkraft ebenso wirkt wie die Schwerkraft (proportional zur Masse), wobei jedoch die
der Erdbeschleunigung g entsprechende Größe ω2r auf sehr
hohe Werte gesteigert werden kann, sodass die Trennung sehr schnell erfolgt. Während z.B. das Milchfett in der Milch unter dem Einfluss der
Schwerkraft nur langsam nach oben (entgegen der Schwerkraft) steigt, wandert es in der Milchzentrifuge (entgegen der Fliehkraft) sehr
schnell in die nahe der Drehachse liegenden Schichten und kann abgezogen werden.
Rotationsenergie und Trägheitsmoment
Die Bewegungsenergie eines rotierenden Körpers setzt sich aus der Bewegungsenergie seiner Massenpunkte
zusammen. Die Formel

lässt sich nur auf einen Körper anwenden, dessen Massenpunkte dieselbe Geschwindigkeit v
besitzen.
 |
Wir werden uns daher zur Berechnung der Rotationsenergie den rotierenden Körper in kleine
Masseteilchen m1, m2, ..., mn zerlegt denken, für jedes von ihnen die Bewegungsenergie
berechnen und diese Energieanteile summieren. |
|
Ein Masseteilchen mi in der Entfernung ri von der Drehachse A hat die
Geschwindigkeit

Seine Bewegungsenergie ist daher

Sind m1, m2, ..., mn alle Masseteilchen des Körpers, so
ist ihre gesamte Bewegungsenergie gegeben durch

Durch Einführung der physikalischen Größe

erhält die Formel für die Rotationsenergie dieselbe Gestalt wie jene für die Bewegungsenergie
bei der Translation.

Da diese Größe J bei der Rotation dieselbe Rolle spielt wie die Gesamtmasse m des
Körpers bei der Translation, also für die Trägheit des Körpers maßgebend ist, heißt sie
Trägheitsmoment des rotierenden Körpers bezüglich der gegebenen Drehachse. Die Einheit des
Trägheitsmoments ist gegeben durch

Während die Gesamtmasse eines Körpers eine unveränderliche Körpereigenschaft darstellt,
ist dies beim Trägheitsmoment nicht der Fall, denn dieses hängt von der Wahl der Drehachse ab. Das Trägheitsmoment ist daher eine
relative Größe; ein Körper kann bei gleichbleibender Masse je nach Wahl der Drehachse unterschiedliche Trägheitsmomente haben.
Man erzielt umso größeres Trägheitsmoment und damit umso größere Rotationsenergie, je weiter die Masseteilchen von der
Drehachse entfernt sind. Bei Schwungrädern ist daher die Masse möglichst weit außen anzubringen.

Schwungrad einer Spielzeugdampfmaschine
(Quelle: "Kids Steam Engine" by Andreas Koppe is licensed under CC BY-NC-SA 2.0,
https://search.creativecommons.org/photos/35d095d0-6150-43e1-b653-c8e187ac10f3, 02.08.2021
Ein rollender Körper führt eine Rotation und eine Translation gleichzeitig aus. Die
Bewegungsenergie ist die Summe der Rotationsenergie und der Bewegungsenergie der Translation. Der folgende Versuch zeigt das.
Auf einer schiefen Ebene rollt ein homogener Vollzylinder schneller herab als ein Hohlzylinder. Von der
Gesamtenergie Ep = m·g·h entfällt beim Hohlzylinder ein größerer Anteil auf die
Rotationsenergie, da hier die Masse durchwegs möglichst weit von der Drehachse entfernt ist, was ein größeres Trägheitsmoment
ergibt.
Die Hauptträgheitsachsen
Für die Drehbewegungen eines starren Körpers sind diejenigen Achsen von besonderem Interesse, die
durch den Schwerpunkt des Körpers gehen.
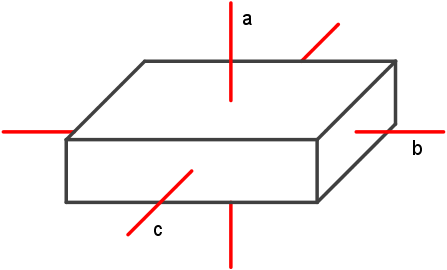
Wenn man z.B. bei einem Quader für eine große Zahl verschiedener Schwerpunktsachsen die
Trägheitsmomente bestimmt, so zeigt sich, dass das Trägheitsmoment für die Achse a den größten und für die
Achse b den kleinsten Wert hat (vgl. obige Abbildung). In ähnlicher Weise gibt es auch für die meisten anderen Körper zwei
zueinander senkrechte Achsen, für die das Trägheitsmoment ein Maximum bzw. ein Minimum ist. Diese Achsen bilden zusammen mit einer dritten,
auf den beiden genannten Achsen senkrecht stehenden Achse die Hauptträgheitsachsen des Körpers.
Die Analogie zwischen Translation und Rotation
Die Analogien zwischen der Translations- und der Rotationsbewegung, die oben im Zusammenhang mit der Masse
und dem Trägheitsmoment angedeutet worden sind, sollen jetzt weiterverfolgt werden. Wir betrachten dabei vorerst nur die Rotation um eine feste
Achse; der Winkelgeschwindigkeitsvektor liegt dann in einer festen Geraden. Dem entspricht die Translation auf einer Geraden; dabei liegt der
Geschwindigkeitsvektor stets in dieser festen Geraden. Somit können wir im Folgenden auf eine Vektordarstellung verzichten und alle
Größen durch ihre Beträge darstellen.
Wir haben früher gezeigt, dass ein Massenpunkt mit der Masse m, der sich auf einer geraden Bahn
bewegt, durch eine Kraft F eine Änderung seiner Bahngeschwindigkeit v, d.h. eine Beschleunigung a, erfährt und dass der
Zusammenhang
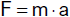
besteht, vorausgesetzt, dass F parallel zu v wirkt. Der Kraft F und der Geschwindigkeit v bei der
Translation entsprechen das Drehmoment M und die Winkelgeschwindigkeit ω bei der Rotationsbewegung. Ein Drehmoment bewirkt eine
Änderung der Winkelgeschwindigkeit. Wir sprechen dann analog zur Bahnbeschleunigung a von einer Winkelbeschleunigung α.
Unter der Winkelbeschleunigung α verstehen wir den Quotienten aus der im Zeitintervall Δt erfolgenden Änderung der
Winkelgeschwindigkeit Δω und dem Zeitintervall Δt.

Die abgeleitete Einheit der Winkelbeschleunigung ist

Diese Definition der Winkelbeschleunigung hat nur einen Sinn, wenn es sich um eine Bewegung handelt, bei der
die Änderung der Winkelgeschwindigkeit Δω proportional zum Zeitintervall Δt ist. Wenn dies nicht der Fall ist, so
sind ähnliche Überlegungen erforderlich wie früher bei der Definition der Bahnbeschleunigung a. Es ergibt sich dann

Für die Winkelgeschwindigkeit gilt aufgrund früherer Feststellungen

und daher

Für die Winkelbeschleunigung ergibt sich

oder

Wenn ein starrer Körper durch ein Drehmoment M in eine Rotationsbewegung versetzt wird, so
können wir diesen Vorgang auch so deuten, dass an jedem Masseteilchen mi des starren Körpers eine zum
Radiusvektor ri des Masseteilchens normale Kraftkomponente Fi angreift, die in einer zur Drehachse normalen Ebene
liegt. Da jede dieser Kräfte das Drehmoment

bewirkt, ergibt sich das auf den starren Körper wirkende Gesamtdrehmoment M durch Addition der
einzelnen Drehmomente. Es ist also
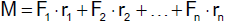
Nach der dynamischen Kraftdefinition gilt ferner für jedes Masseteilchen mi

Daher ist

Die Winkelbeschleunigung α hat bei einem starren Körper für alle Masseteilchen den
gleichen Betrag, sodass
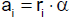
gilt. Für das Gesamtdrehmoment M erhalten wir dann

Die oben erwähnte Analogie zwischen den bei der Translationsbewegung und bei der Rotationsbewegung
auftretenden physikalischen Größen wird erneut deutlich, wenn man die Formeln
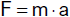 |
und |
 |
miteinander vergleicht. Dabei wird nicht nur die oben genannte Feststellung bestätigt, dass die
Masse m und das Trägheitsmoment J einander entsprechen, dass also das Trägheitsmoment eines Körpers ein Maß für
seinen Widerstand gegen eine Winkelbeschleunigung darstellt, sondern wir erkennen darüber hinaus, dass auch Kraft und Drehmoment sowie
Bahnbeschleunigung und Winkelbeschleunigung analoge Größen darstellen. Es ergibt sich also:
Die Formeln und Gesetze für die Translationsbewegung und die Rotationsbewegung können ineinander
übergeführt werden, indem man die folgenden analogen Größen gegeneinander austauscht:
| |
Translationsbewegung |
|
Rotationsbewegung |
|
 |
 |
 |
 |
 |
| |
Wegstrecke |
 |
Drehwinkel |
 |
 |
 |
 |
 |
 |
| |
Bahngeschwindigkeit |
 |
Winkelgeschwindigkeit |
 |
 |
 |
 |
 |
 |
| |
Bahnbeschleunigung |
 |
Winkelbeschleunigung |
 |
 |
 |
 |
 |
 |
| |
Masse |
 |
Trägheitsmoment |
 |
 |
 |
 |
 |
 |
| |
Kraft |
 |
Drehmoment |
 |
Der Drehimpuls
Unter dem Drehimpuls oder dem Drall (Formelzeichen L) verstehen wir eine abgeleitete physikalische
Größe, die für die Drehbewegung die gleiche Rolle spielt, wie der Impuls für die Translationsbewegung. Wir gehen von der Formel
für den Impuls

aus und ersetzen hierin die Masse m durch das analoge Trägheitsmoment J und die
Geschwindigkeit v durch die analoge Winkelgeschwindigkeit ω. Dann ergibt sich
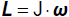
Wir definieren daher: Unter dem Drehimpuls oder dem Drall L eines starren, um
eine feste Achse rotierenden Körpers verstehen wir das Produkt aus seinem Trägheitsmoment J und seiner
Winkelgeschwindigkeit ω. Der Drehimpuls ist ein Vektor, dessen Richtung mit der Richtung der
Winkelgeschwindigkeit zusammenfällt. Als abgeleitete Einheit des Drehimpulses erhalten wir
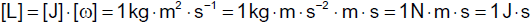
Wir betrachten zunächst einen einfachen Sonderfall.
Ein Massenpunkt mit der Masse m soll sich gleichmäßig auf einem Kreis mit dem Radius r
bewegen. Für das Trägheitsmoment gilt dann
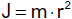
Für den Drehimpuls des Massenpunktes erhalten wir

oder in Vektorschreibweise

Der Drehimpuls für einen ausgedehnten starren Körper ergibt sich, indem wir uns den Körper in
eine große Zahl kleiner Massenelemente mi zerlegt denken, für jedes dieser Massenelemente den Drehimpuls

bestimmen und alle diese Drehimpulse addieren. Damit erhalten wir

Für den Drehimpuls gilt ebenfalls ein Erhaltungssatz in Analogie zur Erhaltung der
Bewegungsgröße bei Translationsbewegungen. Wir zeigen dies für das obige Beispiel des Massenpunktes auf einer Kreisbahn, wobei wir
hier zur Differentialschreibweise übergehen müssen. Betrachten wir dazu die Gleichung

Durch Differentiation erhalten wir

Wegen
 |
und |
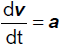 |
ergibt sich
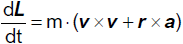
Wegen

erhalten wir

woraus mit
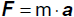
schlussendlich

folgt. Die zeitliche Änderung des Drehimpulses dL/dt entspricht also dem
wirkenden Drehmoment M. Ist insbesondere das wirkende
Drehmoment M = 0, so folgt
dL/dt = 0 bzw. L = konst.
Damit können wir den folgenden Erhaltungssatz formulieren:
| |
In einem gegen die Einwirkung äußerer Drehmomente abgeschlossenen System von
Massenpunkten ist der Gesamtdrehimpuls L (die Summe aller Drehimpulse) nach Betrag und Richtung zeitlich
konstant. |
|
Dabei muss hervorgehoben werden, dass nicht nur der Betrag des Drehimpulsvektors, sondern auch seine Richtung
erhalten bleibt. Da der Drehimpulsvektor auf die Bahnebene normal steht, muss also auch die Lage der Bahnebene unverändert bleiben. Dies wirkt
sich unter anderem dahingehend aus, dass die Planeten bei ihrer Bewegung um die Sonne ihre Bahnebene beibehalten.
Der Drehimpulserhaltungssatz kann durch folgende Experimente (z.B. mit einem Drehschemel) anschaulich
demonstriert werden.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/den-rechten-arm-trainieren_76809, 05.08.2021)
Eine auf einer drehbaren Scheibe befindliche Person hält in einer Hand ein drehbares Rad mit
möglichst großem Trägheitsmoment, wobei die Radachse parallel zur Drehachse der Scheibe verläuft. Zu Beginn des Versuches
befinden sich alle Teile des Systems in Ruhe, sodass sein Drehimpuls Null ist. Die Person setzt nun das Rad mit der freien Hand in Bewegung. Als Folge
der Erhaltung des Drehimpulses gerät die Scheibe dann ebenfalls in Drehbewegung, und zwar im entgegengesetzten Sinn wie das Rad. Auf das System
haben keine äußeren Drehmomente gewirkt, sodass der Gesamtdrehimpuls den Wert Null behalten muss.

(Quelle: Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/den-rechten-arm-trainieren_76809, 05.08.2021,
Icons erstellt von Pixel perfect, https://www.flaticon.com/de/kostenloses-icon/messen_3337019, 04.04.2021)
Eine Person auf einer drehbaren Scheibe hält mit ausgestreckten Armen zwei Massenstücke mit
möglichst großer Masse. Die Scheibe wird von außen in langsame Rotation versetzt. Nachdem dies geschehen ist, zieht die Person
ruckartig die Arme mit den Massenstücken an. Es zeigt sich, dass die Drehbewegung der Scheibe merklich schneller wird. Die Erklärung ergibt
sich aus der Tatsache, dass das Trägheitsmoment durch das Anziehen der Arme kleiner geworden ist. Da der Drehimpuls konstant bleibt, muss die
Winkelgeschwindigkeit entsprechend größer werden.
Der Kreisel
Unter einem Kreisel verstehen wir einen starren, rotierenden Körper, der entweder ganz frei beweglich
ist oder der bei völliger Drehfreiheit nur in einem Punkt festgehalten wird. Insbesondere betrachten wir in diesem Abschnitt symmetrische
Kreisel, also starre und rotationssymmetrische Körper.

Experimentierkreisel der Lehrmittelfirma Leybold
(Quelle: https://www.leybold-shop.at/physik/geraete/mechanik/rotationsbewegungen/kreisel/kreisel/34820.html,
05.08.2021)
Der kräftefreie, symmetrische Kreisel
Ein Kreisel heißt kräftefrei, wenn auf ihn keine äußeren Kräfte einwirken. In der
folgenden Abbildung ist ein solcher Kreisel dargestellt. Dabei muss der Unterstützungspunkt genau im Schwerpunkt S des rotierenden
Körpers liegen.

(Quelle: https://expvorl.physik.uni-muenchen.de/versuche_mechanik/drehbewegungen/kraftefreier_kreisel/index.html, 07.08.2021)
Der Kreiselkörper befindet sich dann im indifferenten Gleichgewicht, wovon man sich durch Aufsetzen des
nicht rotierenden Kreiselkörpers überzeugen kann. Wird der Kreisel in rasche Rotation um seine Figurenachse versetzt und durch den Raum
bewegt, so behält die Figurenachse ihre Richtung im Raum bei.
Der nicht kräftefreie, symmetrische Kreisel
Wir setzen einen schnell rotierenden Kreisel auf eine horizontale Unterlage.

Der Kreisel fällt nicht herab, seine Achse bewegt sich vielmehr langsam auf einem Kegelmantel. Diese
Bewegung heißt Präzessionsbewegung des Kreisels. Die folgende Abbildung erklärt das Zustandekommen der Präzessionsbewegung. Die
Kreiselachse ist dabei in einer Schlinge aufgehängt.

"Fahrradkreisel"
(Quelle: https://www.av.ph.tum.de/Experiment/1000/
Beschreibungen/ver1306.php, 01.08.2021) |
 |
Der Kreisel hat den Drehimpuls L. Das von G und
−G hervorgerufene Drehmoment M erzeugt in einem kleinen Zeitintervall Δt
eine zu M gleichgerichtete
Drehimpulsänderung ΔL = M·Δt. Der daraus resultierende
Gesamtdrehimpuls des Kreisels L+ΔL hat unveränderten Betrag, da
ΔL für Δt → 0 stets zu L normal ist. Es erfolgt aber eine
ständige Änderung der Richtung von L. Der Drehimpulsvektor des Kreisels und damit die
Kreiselachse führt eine Präzessionsbewegung aus.
Literatur:
Höfling, Oskar: Physik - Lehrbuch für Unterricht und Selbststudium, 15. Aufl., Ferd. Dümmlers Verlag, Bonn 1987
Westphal, Wilhelm H.: Physik, 25./26. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1970
Gerthsen, Christian / Kneser, Hans Otto / Vogel, Helmut: Physik, 14. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1982
Tipler, Paul A. / Mosca, Gene: Physik für Wissenschaftler und Ingenieure, 6. Aufl., Spektrum Akademischer Verlag, Heidelberg 2009
Dobson, Ken / Grace, David / Lovett, David: Physics, Published by HarperCollinsPublishers Limited, London 2002
Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969
Schreiner, Josef: Lehrbuch der Physik 2. Teil, 1. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1964