Aus Gründen der besseren Lesbarkeit wird im Folgenden die Sprachform des generischen Maskulinums verwendet. Es wird an dieser Stelle darauf hingewiesen, dass die ausschließliche Verwendung der männlichen Form geschlechtsunabhängig verstanden werden soll.

Nikolaus Kopernikus, De revolutionibus orbium coelestium (Über die Umlaufbahnen der Himmelssphären), Nürnberg 1543
(Quelle: "Bildnis des Copernicus Nicolaus" by ubleipzig is marked with CC PDM 1.0,
https://wordpress.org/openverse/image/43014e11-9bf0-48fa-a611-5b86459bfd68, 15.03.2022
"Heliocentric Diagram from 'De Revolutionibus'" by University of Glasgow Library is licensed under CC BY-NC-SA 2.0
https://search.creativecommons.org/photos/8aff8339-079c-4eb7-a4f7-bb9e9bf304cd, 15.08.2021)

1.		Das geozentrische Weltbild
2.		Das heliozentrische Weltbild
3.		Die Keplerschen Gesetze – Teil 1
4.		Das Gravitationsgesetz
5.		Das Gravitationsfeld einer Kugelmasse
6.		Die Keplerschen Gesetze – Teil 2
7.		Satelliten
8.		Die Achsendrehung der Erde
9.		Die Erde und ihr Mond

Im Folgenden werden Vektoren mit kursiven Fettbuchstaben dargestellt. Der Betrag eines Vektors wird (sofern nicht anders angegeben) mit demselben Buchstaben in nicht kursiver Normalschrift bezeichnet, z.B. |a| = a.

1. Das geozentrische Weltbild

Das geozentrische Weltbild (griech. γεοκεντρικός, geokentrikós, erdzentriert) lässt die Erde und damit auch den Menschen im Universum eine zentrale Position einnehmen. Bis ins Mittelalter wurde die als ruhend angenommene Erde als Bezugssystem zur Beschreibung des astronomischen Geschehens verwendet. Da wir von der Bewegung der Erde (Erdrotation) nichts spüren, ist dies die Beschreibung des Geschehens, wie wir es unmittelbar mit unseren Sinnen wahrnehmen. Wir sind natürlich heute nicht mehr davon überzeugt, dass die Erde ruht, da es uns grundsätzlich nicht möglich ist, ein absolut ruhendes Bezugssystem anzugeben. Da wir jedoch unser Bezugssystem frei wählen können, ist die Beschreibung der Bewegungen der Himmelskörper bezüglich der Erde nicht unbedingt falsch.

1.1  Hipparchos von Nicäa (Phantasiebild) (Quelle: https://commons.wikimedia.org/wiki/File:Hipparchos_1.jpeg, 20.08.2021)

1.2  Klaudios Ptolemaios (neuzeitliches Idealporträt) (Quelle: https://commons.wikimedia.org/wiki/File:PSM_V78_D326_Ptolemy.png, 20.08.2021)

Das geozentrische Weltbild wurde vorwiegend von Hipparchos von Nicäa (etwa 190 – 120 v. Chr.), dem bedeutendsten griechischen Astronomen seiner Zeit, begründet. Eine Darstellung dieses Weltensystems hat Klaudios Ptolemaios (etwa 100 – 160 n. Chr.) in seinem Hauptwerk "Almagest", einer Abhandlung zur Mathematik und Astronomie in 13 Büchern, gegeben. Dieses Werk blieb bis zum Ende des Mittelalters das Standardwerk der Astronomie im europäischen Raum. Es enthält neben einem ausführlichen Sternenkatalog eine detaillierte Ausarbeitung des geozentrischen Weltbilds, das daher später nach ihm ptolemäisches Weltbild genannt wurde. Im Folgenden sollen einige wesentliche Punkte dieses Systems dargestellt werden.

Das Himmelsgewölbe hat Kugelgestalt und dreht sich um die ruhende Erde.

In einer klaren, dunklen Nacht können wir weitab von jeder "Lichtverschmutzung" mit bloßem Auge rund 3000 bis 5000 Sterne am Himmel wahrnehmen. Diese Sterne ändern ihre gegenseitige Lage nicht merklich und werden daher als Fixsterne bezeichnet. Da wir die Unterschiede zwischen ihren durchwegs enorm großen Entfernungen von der Erde nicht beobachten können, erscheinen sie uns in gleicher Entfernung, als ob sie an einer Kugelschale, dem Himmelsgewölbe, fixiert wären. Sie können daher teilweise zu sogenannten Sternbildern zusammengefasst werden (vgl. Abbildung 1.3).

1.3  Nördlicher Fixsternhimmel (Ausschnitt); Sternbilder sind durch Linien hervorgehoben; die uns am hellsten erscheinenden Sterne tragen Namen
(Quelle: Erstellt mit Stellarium 0.21.3 - https://stellarium.org/de/, 07.03.2022)

Auch wenn sich die gegenseitige Lage der Fixsterne nicht ändert, so stehen sie doch bezüglich der Erde nicht still. Sie bewegen sich alle auf Kreisbahnen um eine gemeinsame Achse, das ganze Himmelsgewölbe mit den Fixsternen dreht sich um diese Himmelsachse. Diese Achse trifft das Himmelsgewölbe in den Himmelspolen (vgl. Abbildung 1.4).

1.4  Himmelsgewölbe, Himmelsachse, Himmelspole
(Quelle: Icons erstellt von turkkub, https://www.flaticon.com/de/kostenloses-icon/weltweit_814513, 06.04.2022)

Der Himmelsnordpol wird annähernd durch den Polarstern markiert. Die Dauer einer vollen Umdrehung des Himmelsgewölbes (und damit irgendeines Fixsternes) heißt 1 Sterntag. Der Sterntag bildet die Basis der sogenannten Sternzeit, einer in Astronomie und Geodäsie verwendeten Zeitskala. Ein mittlerer Sterntag dauert etwa 23 Stunden 56 Minuten 4 Sekunden (also nicht 24 Stunden) und ist damit um rund 1 / 365 kürzer als ein mittlerer Sonnentag, auf dem der übliche Kalendertag beruht.

1.5  Drehung des Himmelsgewölbes (Sterntag) (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

1.6  Photographie des nördlichen Fixsternhimmels mit einer Belichtungszeit von ca. 1,6 Stunden; alle Fixsterne beschreiben konzentrische
Kreisbahnen; die Rotationsachse (Himmelsachse) geht durch den Himmelsnordpol; der Polarstern ist vom Himmelsnordpol etwa 1° entfernt
und hat sich während der Aufnahme kaum bewegt
(Quelle: "Startrails over the Autumn foliage" by Darron Birgenheier is licensed with CC BY-SA 2.0,
https://search.creativecommons.org/photos/78a27a8e-77a2-4d0c-8cd5-84f3602c77c0, 22.08.2021)

Die Erde ist gegenüber dem Radius des Himmelsgewölbes punktförmig klein und befindet sich im Mittelpunkt des Himmelsgewölbes.

Diese These folgt aus der Tatsache, dass der Winkel zwischen zwei Sternen zu jeder Zeit und an jedem Ort der Erde derselbe ist. Von verschiedenen Punkten einer gegen das Himmelsgewölbe nicht punktförmig kleinen Erde müssten zwei Sterne unter verschiedenen Winkeln gesehen werden. Von einer nicht im Mittelpunkt des Himmelsgewölbes ruhenden Erde müssten zwei Sterne im Laufe einer Umdrehung des Himmelsgewölbes unter verschiedenen Winkeln erscheinen (vgl. Abbildung 1.7).

1.7  Erde nicht punktförmig klein bzw. nicht im Mittelpunkt des Himmelsgewölbes
(Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

Die durch den Standort eines Beobachters an die Erde gelegte Tangentialebene nennen wir den scheinbaren Horizont des Beobachters. Es zeigt sich, dass dieser scheinbare Horizont das Himmelsgewölbe stets halbiert, als ob er durch den Mittelpunkt der Erde ginge (wahrer Horizont).

1.8  Himmelsgewölbe und Erde (übertrieben groß gezeichnet); Himmelsäquator; Beobachter B in der
geographischen Breite φ und dessen wahrer Horizont; Polhöhe φ' = geographische Breite (als Normalwinkel)
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 249)

Das ist ein weiterer Beweis für die im Vergleich zum Himmelsgewölbe vernachlässigbar kleinen Abmessungen der Erde und für ihre Stellung im Mittelpunkt des Himmelsgewölbes. Als Beispiel für die äußerst folgerichtige Darstellung der Verhältnisse durch Ptolemaios ist im Folgenden der betreffende Abschnitt aus seinem Werk (Buch 1, Kap. 6, "Die Erde steht zu den Himmelskörpern in dem Verhältnis eines Punktes") wiedergegeben.

	"Daß die Erde zu der Entfernung bis zu der Sphäre der sogenannten Fixsterne für die sinnliche Wahrnehmung wirklich nur in dem Verhältnis eines Punktes steht, dafür ist ein zwingender Beweis, daß von allen ihren Teilen aus die scheinbaren Größen und gegenseitigen Abstände der Sterne zu denselben Zeiten allenthalben gleich und ähnlich sind, wie denn auch die in verschiedenen geographischen Breiten an denselben Sternen angestellten Beobachtungen auch nicht im geringsten voneinander abweichend gefunden werden. Als ganz besonders bezeichnend ist auch noch der Umstand hervorzuheben, daß die (Endpunkte der) an beliebiger Stelle der Erde aufgestellten Gnomonen sowie die Mittelpunkte der Armillarsphären dieselbe Geltung haben wie der wirkliche Mittelpunkt der Erde, d.h. daß die genannten Punkte für die Richtung der Visierlinien (nach den Himmelskörpern) und für die Herumleitung der Schattenlinien in so großer Übereinstimmung mit den zur Erklärung der Himmelserscheinungen aufgestellten Hypothesen maßgebend sind, wie wenn diese Linien direkt durch den Mittelpunkt der Erde gingen. Ein deutliches Anzeichen dafür, daß dieses Größenverhältnis besteht, liegt auch in dem Umstand, daß die durch das Auge gelegten Ebenen, die wir Horizonte nennen, überall stets die ganze Himmelskugel halbieren, was nicht der Fall sein würde, wenn die Größe der Erde im Verhältnis zur Entfernung der Himmelskörper ein merkbarer Faktor wäre. Alsdann könnte nur die durch den Punkt im Zentrum der Erde gelegte Ebene die Himmelskugel halbieren, während die durch beliebige Punkte der Erdoberfläche gelegten Ebenen die unter der Erde liegenden Abschnitte größer machen würden als die über der Erde befindlichen."
	(Quelle: Des Claudius Ptolemäus Handbuch der Astronomie, erster Band, aus dem Griechischen übersetzt und mit erklärenden Anmerkungen versehen von Karl Manitius, Druck und Verlag von B. G. Teubner Leipzig 1912, 09.03.2022)

Den Winkel zwischen dem Horizont und der Richtung nach einem bestimmten Gestirn nennen wir die Höhe des Gestirnes. Die Höhe eines Himmelspols heißt speziell die Polhöhe. Während sich die Höhe eines beliebigen Gestirnes für einen bestimmten Beobachter im Laufe der Zeit ändert (das Gestirn beschreibt ja eine Kreisbahn um die Himmelsachse), bleibt die Polhöhe unverändert. Wenn die Erde Kugelgestalt hat, muss gelten: Die Polhöhe ist gleich der geographischen Breite (vgl. Abbildung 1.8).
Tatsächlich beobachtet man beim Fortschreiten entlang der Erdoberfläche in der Nordrichtung (sie wird durch den Himmelsnordpol angezeigt) eine zum Weg proportionale Zunahme der Polhöhe. Bezeichnet s den in Nordrichtung zurückgelegten Bogen auf der Erdoberfläche, R den Erdradius und Δφ die beobachtete Zunahme der Polhöhe, d.h. die Änderung der geographischen Breite, so kann aus der Beziehung

der Erdradius R gefunden werden. Schon der griechische Mathematiker Eratosthenes hat um 200 v. Chr. die Länge des Meridianbogens zwischen Alexandria und Syene (Assuan) aus der Dauer einer Reise zwischen diesen Orten abgeschätzt und daraus den Erdradius berechnet. Der Fehler betrug nur ca. 4%.

Da die Erde im Mittelpunkt des Himmelsgewölbes steht, ist die Himmelsachse auch Erdachse. Die durch den Erdäquator gelegte Ebene schneidet das Himmelsgewölbe im Himmelsäquator (vgl. Abbildung 1.8). So wie man auf der Erdoberfläche die Lage eines Punktes durch seine geographische Länge und Breite angibt, so kann man auch auf dem Himmelsgewölbe die Lage eines Gestirnes durch Einführung eines ganz analog aufgebauten Kreisnetzes angeben. Man kann dann Sternkarten durch dieselben Projektionsverfahren herstellen, mit denen man Karten der Erdoberfläche gewinnt. Obwohl uns heute bekannt ist, dass die Entfernungen der Fixsterne von der Erde sehr verschieden sind, hat damit die Vorstellung eines Himmelsgewölbes mit daran fixierten Sternen damit doch noch ihre Berechtigung. Betrachten wir dazu das Sternbild Orion (vgl. Abbildung 1.9).

1.9  Sternbild Orion
(Quelle: Erstellt mit Stellarium 0.21.3 - https://stellarium.org/de/, 07.03.2022)

In diesem Sternbild ist der Stern Bellatrix (lat. Kriegerin) in der rechten Schulter ca. 243 Lichtjahre von der Erde entfernt. Der Stern Hatysa (arab. Nair Al Saif, der Helle im Schwert) besitzt mit 1325 Lichtjahren die mehr als 5fache Entfernung. Bei Betrachtung am Himmelsgewölbe scheinen die beiden Sterne jedoch gleich weit von der Erde entfernt zu sein.

Die natürlichste Bewegung ist die Kreisbewegung. Alle Bewegungen der Himmelskörper lassen sich aus Kreisbewegungen zusammensetzen.

Diese These des ptolemäischen Weltbildes bezieht sich auf die Bewegungen der Sonne und der Planeten. Schon oberflächliche Beobachtung zeigt, dass die Sonne nicht genau die Bewegung des Fixsternhimmels mitmachen kann. Sie müsste (für einen bestimmten Beobachtungsort) sonst täglich am selben Punkt des Horizontes auf- und untergehen, wie das jeder Fixstern tut. Ihre Höhe im Kulminationspunkt (das ist der Winkel zwischen der Richtung nach der Sonne und dem Horizont zur Zeit des Sonnenhöchststands) dürfte sich im Laufe eines Jahres nicht ändern. Die Umlaufzeit der Sonne ist aber um etwa 4 Minuten länger als ein Sterntag. Die Zeit zwischen zwei aufeinanderfolgenden Kulminationen der Sonne heißt ein wahrer Sonnentag. Messungen zeigen außerdem, dass diese wahren Sonnentage untereinander nicht gleich lang sind.
Die Sonne bleibt also gegenüber der Bewegung des Fixsternhimmels ständig zurück und durchwandert dabei im Laufe eines Jahres gegenüber dem Fixsternhimmel eine Kreisbahn, die sogenannte Ekliptik. Die Ebene dieser Kreisbahn ist aber nicht normal zur Himmelsachse, sie ist gegen den Himmelsäquator um etwa 23° 27' geneigt (vgl. Abbildung 1.10).

1.10  Himmelsäquator, Ekliptik mit Tierkreisgürtel, Frühlingspunkt (F) und Herbstpunkt (H)
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 250)

Die Ekliptik wird in 12 Teile geteilt und jedem Teil das dort liegende Sternbild des Tierkreisgürtels zugeordnet. Jeder Zeit des Jahres ist also die Stellung der Sonne in einem dieser Sternbilder zugeordnet. Die Ekliptik schneidet den Himmelsäquator im Frühlingspunkt (Stand der Sonne am 21. 3.) und im Herbstpunkt (Stand der Sonne am 23. 9.). An diesen Tagen wandert die Sonne (bezüglich der Erde) in unmittelbarer Nähe des Himmelsäquators, Tag- und Nachtbogen sind gleich lang, es herrscht Tag- und Nachtgleiche. Die Bewegung der Sonne (bezüglich der Erde) kann also aus Kreisbewegungen um die Weltachse (sie erfolgen von Osten gegen Westen, jeder Umlauf dauert einen Sterntag) und einer zusätzlichen jährlichen Kreisbewegung entlang der Ekliptik (sie erfolgt entgegen der täglichen Rotation) zusammengesetzt werden. Während die Sonne die Ekliptik (bezüglich des Fixsternhimmels) einmal durchläuft, vollführt das Himmelsgewölbe rund 366,25 Umdrehungen, das Jahr hat also 366,25 Sterntage; es hat aber, da die Sonne im Laufe des Jahres um einen vollen Umlauf zurückbleibt, nur 365,25 Sonnentage. Die jährliche Bewegung der Sonne (bezüglich der Erde) ist einer Schraubenlinie (mit veränderlicher Ganghöhe) ähnlich.

Seit dem Altertum sind einige "Sterne" bekannt, die ihre Lage am Fixsternhimmel verändern und daher als Wandelsterne oder Planeten bezeichnet werden. Bis ins Mittelalter waren nur die Planeten Merkur, Venus, Mars, Jupiter und Saturn bekannt. Die Bewegung der Planeten bezüglich des Fixsternhimmels ist sehr verschiedenartig. Der Betrag der Bahngeschwindigkeit ist nicht konstant. Es kann zu gewissen Zeiten Stillstand eintreten, es kommen Schlingenbildungen und rückläufige (retrograde) Bewegungen vor. Die Animationen 1.11 und 1.12 zeigen zwei Beispiele.

1.11  Schlingenbildung
1.12  Rückläufige (retrograde) Bewegung

Kann die Bewegung der Sonne aus der Bewegung des Fixsternhimmels (1 Umdrehung pro Sterntag) und einer Kreisbewegung entlang der Ekliptik (1 Umlauf pro Jahr) zusammengesetzt werden, so lassen sich die komplizierten Bewegungen der Planeten in guter Näherung ebenfalls aus Kreisbewegungen zusammensetzen.

Die Epizykeltheorie

In der Epizykeltheorie bewegt sich ein Stern (Planet) auf einer kleinen Kreisbahn (Epizykel, Aufkreis), die ihrerseits auf einer großen Kreisbahn (Deferent, Trägerkreis) um einen festen Mittelpunkt wandert. Der Epizykel ist daher ein "auf einem Kreis kreisender Kreis". Diese Theorie wurde vermutlich von Apollonios von Perge gegen Ende des 3. Jahrhunderts v. Chr. aufgestellt und war in der Astronomie bis ins 17. Jahrhundert vorherrschend. Mit dieser Theorie konnte begründet werden, warum sich die Planeten gegenüber dem Fixsternhimmel mit variierender Geschwindigkeit bewegen. Im ptolemäischen Weltbild erfolgte ein systematischer Ausbau der Theorie. Dabei wurde die Epizykeltheorie schon von Ptolemaios mit der Exzentertheorie von Hipparchos verbunden, in der die Erde gegenüber dem Zentrum des Deferenten versetzt ist. Ferner führte Ptolemaios den Äquanten (Ausgleichspunkt) ein, einen Punkt, der von der Erde aus hinter dem Mittelpunkt des Deferenten liegen sollte, aber doppelt so weit entfernt wie dieser. Der Grundgedanke von der Gleichförmigkeit der Kreisbewegung wurde auf den Äquanten angewendet. Der Epizykelmittelpunkt sollte auf dem Deferenten gerade so umlaufen, dass seine Bewegung nicht vom Mittelpunkt des Deferenten, sondern vom Äquanten aus gesehen gleichförmig erscheinen würde.
In der Animation 1.13 bewegt sich der rote Punkt (entspricht dem Mittelpunkt des Epizykels) vom Mittelpunkt des strichlierten Kreises (entspricht dem Äquanten) aus gesehen gleichförmig (mit konstanter Winkelgeschwindigkeit). Vom Mittelpunkt des durchgezogenen Kreises (entspricht dem Mittelpunkt des Deferenten) aus gesehen erfolgt diese Bewegung jedoch nicht gleichförmig.

1.13  Gleichförmige Bewegung bezüglich des Äquanten

Die Abbildung 1.14 zeigt die Darstellung von Deferent und Epizykel nach Ptolemaios. Im Centrum Mundi befindet sich die punktförmige Erde. Um die Exzentrizität des Planeten versetzt, befindet sich darüber das Centrum Deferentis. Im gleichen Abstand liegt darüber das Centrum Equantis. Von diesem Punkt aus bewegt sich der Epizykel mit konstanter Winkelgeschwindigkeit auf dem Deferenten. Die strichlierte Linie zeigt den wahren Ort des Planeten auf der Ekliptik.

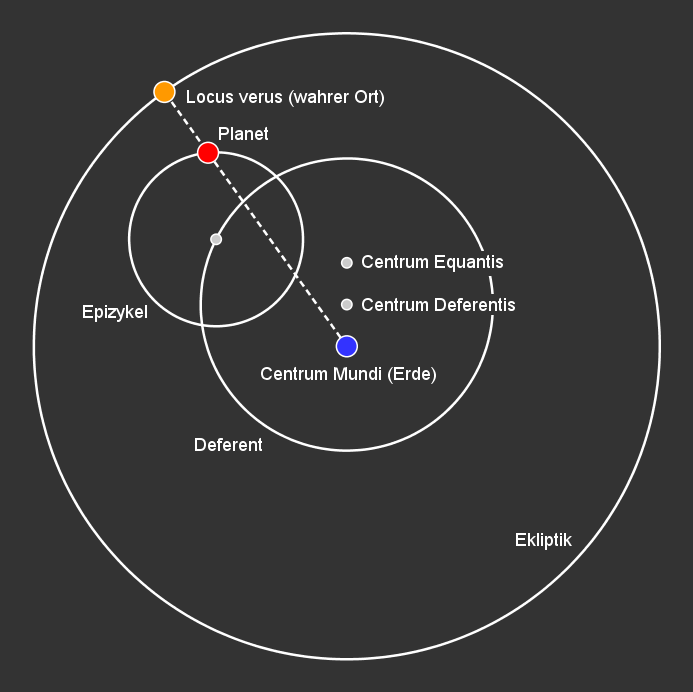
1.14  Deferent und Epizykel nach Ptolemaios

Damit ist es möglich, z.B. die Schlingenbildung der Planetenbewegung zu erklären (vgl. Animation 1.15).

1.15  Schlingenbildung einer Planetenbewegung in der Epizykeltheorie

Auch im heliozentrischen Weltbild nach Nikolaus Kopernikus wurden noch Epizykel eingesetzt, wobei die Deferenten für die Planeten nun die mittlere Sonne zum Mittelpunkt hatten. Die Epizykeltheorie wurde erst von Johannes Kepler mit der Theorie der ellipsenförmigen Planetenbahnen abgelöst. Bemerkenswert ist jedoch, dass mit Epizykeln (bei entgegengesetztem Drehsinn) auch eine exakt elliptische Bahn beschrieben werden kann (vgl. Animation 1.16). Befindet sich die Sonne in einem der Brennpunkte der Ellipse, so würde der Äquant im anderen Brennpunkt liegen und nach dem zweiten Keplerschen Gesetz tatsächlich die Eigenschaft zeigen, dass von ihm aus gesehen die Winkelgeschwindigkeit des Umlaufs in den Bereichen der Sonnennähe und der Sonnenferne gleich ist.

1.16  Ellipsenförmige Planetenbahn in der Epizykeltheorie

2. Das heliozentrische Weltbild

Einer der Ersten, der das heliozentrische Weltbild (griech. ἥλιος, helios, Sonne und κέντρον, kentron, Zentrum) vertrat, wonach die Sonne und nicht die Erde im Zentrum steht, war der griechische Astronom und Mathematiker Aristarch(os) von Samos (~310 v. Chr. – ~230 v. Chr.).

2.1  Denkmal Aristarchs an der Aristoteles-Universität Thessaloniki, Griechenland (Quelle: https://commons.wikimedia.org/wiki/File: Aristarchos_von_Samos_(Denkmal).jpeg, 13.03.2022)

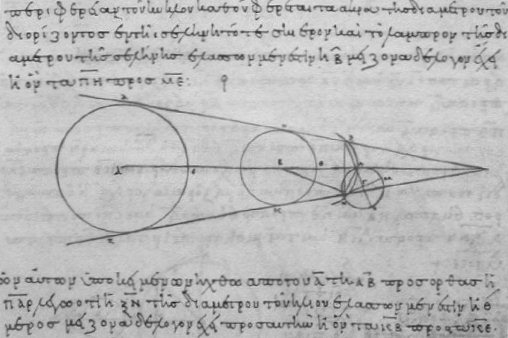
2.2  Aristarchs Berechnungen der Größen von Erde, Sonne und Mond (Abschrift aus dem 10. Jahrhundert) (Quelle: https://commons.wikimedia.org/wiki/File:Aristarchus_working.jpg, 10.03.2022)

Das einzige erhaltene Werk Aristarchs trägt den Titel "Über die Größen und Abstände von Sonne und Mond" und basiert noch auf dem geozentrischen Weltbild. Durch spätere Zitate ist bekannt, dass er in einem anderen Buch auch die Hypothese eines heliozentrischen Weltbildes vertrat. Aristarch gelang eine Abschätzung der Größen- und Entfernungsverhältnisse von Erde, Mond und Sonne. Den Erddurchmesser konnte Aristarch mit dem Monddurchmesser vergleichen, als während einer partiellen Mondfinsternis ein Teil des Erdschattens auf den Mond fiel (vgl. Abbildung 2.3).

2.3  Partielle Mondfinsternis (Mehrfachbelichtung)
(Quelle: "How big is Earth compared to Moon?" by Petr Hykš is marked with CC BY-NC 2.0,
https://wordpress.org/openverse/image/fe7847d7-1ba5-4e29-8e5f-e30faa33332a, 09.03.2022)

Wegen der großen Sonnenentfernung durfte er annehmen, dass der Durchmesser des Erdschattens sich bis zum Mond nur wenig verändert, also auch auf dem Mond ungefähr gleich dem Erddurchmesser ist (vgl. Abbildung 2.4).

2.4  Bestimmung des Größenverhältnisses von Erd- und Monddurchmesser

Den auf dem Mond sichtbaren Teil des Erdschattens verglich er mit dem Monddurchmesser. Er fand, dass der Durchmesser der Erde 2,85-mal so groß ist wie der des Mondes. Tatsächlich beträgt dieser Faktor etwa 3,67. Aristarch erkannte, dass der Halbmond dadurch entsteht, dass das Sonnenlicht genau senkrecht zu unserer Blickrichtung auf den Mond fällt. Das Dreieck Sonne, Mond, Erde weist also bei Halbmond einen rechten Winkel auf (vgl. Abbildung 2.5).

2.5  Bestimmung der Entfernungsverhältnisse von Erde, Mond und Sonne

Die Größe des Winkels ε zwischen Sonne und Mond bestimmte Aristarch experimentell zu mindestens 87°. Durch Zeichnen eines rechtwinkligen Dreiecks mit einem Winkel von 87° lässt sich nun das Verhältnis der Abstände Erde – Sonne und Erde – Mond bestimmen. Aristarch kam zu der Überzeugung, dass die Sonne mindestens 19-mal so weit von der Erde entfernt ist wie der Mond. Tatsächlich ist die Sonne etwa 400-mal so weit von der Erde entfernt wie der Mond. Das entspricht einem Winkel ε von etwa 89°51'. Das heißt, dass von der Sonne aus gesehen Erde und Mond nur knapp neun Winkelminuten voneinander entfernt erscheinen. Da uns die Sonne fast ebenso groß erscheint wie der Mond (bei einer totalen Sonnenfinsternis verdeckt der Mond gerade die Sonne, vgl. Abbildung 2.6) und zudem von der Erde viel weiter entfernt ist als der Mond, muss sie sehr viel größeren Durchmesser als die Erde haben.

2.6  Totale Sonnenfinsternis
(Quelle: "Solar Eclipse August 21st 2017 in Tennessee USA" by Seánín Óg is marked with CC BY-NC-ND 2.0
https://wordpress.org/openverse/image/fae806cc-b01d-49ca-b0f1-842bddcc273f)

Diese fundamentale Erkenntnis von der außerordentlichen Größe der Sonne (und damit von der Kleinheit der Erde) war für Aristarch die Grundlage einer revolutionären Idee: Nicht die viel größere Sonne bewegt sich um die kleine Erde, sondern die Sonne ist der Mittelpunkt der Welt. Diese Idee konnte sich aber nicht durchsetzen, und es ist nicht bekannt, ob nicht Aristarch selbst sie später verworfen hat. So geriet seine Idee für ca. 1700 Jahre in Vergessenheit.

Das geozentrische Weltbild war viele Jahrhunderte lang die vorherrschende und allgemein anerkannte Lehrmeinung, jedoch wurden immer mehr Unzulänglichkeiten des ptolemäischen Systems erkannt. Eine Reihe von astronomischen Beobachtungen konnte mit dem geozentrischen Weltbild nicht widerspruchsfrei erklärt werden. Außerdem war die Genauigkeit der Berechnungen für die Seefahrt und auch für den Kalender nicht mehr ausreichend. Um diese Probleme zu lösen, versuchte man das Weltbild des Ptolemaios immer weiter auszubauen. Es wurde dadurch auch immer komplizierter. So bedurfte es in der Epizykeltheorie zur Berechnung der Bewegungen von Sonne, Mond und Planeten komplizierter Konstruktionen von bis zu 80 mehrstufig zusammengesetzter Kreisbewegungen fiktiver Punkte im Raum. Ungeachtet dessen ließ die Genauigkeit dieser Berechnungen zu wünschen übrig. Zunehmend wurden auch Zweifel an der Richtigkeit dieses Weltbildes laut.

2.7  Nikolaus Kopernikus (1473 – 1543)		2.8  De revolutionibus orbium coelestium (Über die Umlaufbahnen der Himmelssphären)
(Quelle: "Bildnis des Copernicus Nicolaus" by ubleipzig is marked with CC PDM 1.0, https://wordpress.org/openverse/image/43014e11-9bf0-48fa-a611-5b86459bfd68, 15.03.2022 "Astronomiskt verk ur Copernicus bibliotek" by UppsalaUniLib is marked with CC0 1.0, https://wordpress.org/openverse/image/07eec0e7-4d02-47dd-8d10-9891f27b9e54, 15.03.2022)

Nikolaus Kopernikus stieß auf der Suche nach Vereinfachung und Verbesserung des ptolemäischen Systems auf das heliozentrische Modell, das ihm von altgriechischen Quellen bekannt war. Er skizzierte es erstmals in seinem etwa um 1510 geschriebenen "Commentariolus" (vgl. Abbildung 2.9).

2.9  Nicolai Copernici de hypothesibus motuum coelestium a se constitutis commentariolus
Nikolaus Kopernikus' kleiner Kommentar über die Hypothesen der Bewegungen der Himmelskörper, die von ihm selbst aufgestellt wurden
(Quelle: https://commons.wikimedia.org/wiki/File:Commentariolus_Wien_MS10530_Blatt_34.png, 10.03.2022)

Nach mehr als 30jähriger Arbeit stellte er das heliozentrische Weltbild in seinem 1543 im Druck erschienenen Hauptwerk "De revolutionibus orbium coelestium" (Über die Umlaufbahnen der Himmelssphären) zusammenfassend dar. Die Vereinfachung gegenüber dem geozentrischen System kommt in den folgenden Punkten zum Ausdruck.

Die Sonne steht im Mittelpunkt der Welt. Sie ändert ihren Ort nicht. Die Fixsterne stehen in der im Verhältnis zur Erdgröße unermesslich großen kugelförmigen Fixsternsphäre. Sie bewegen sich ebenfalls nicht.

Der wesentliche, durch Kopernikus bewirkte Wandel (Paradigmenwechsel – kopernikanische Wende) in der Physik besteht damit in der Einführung eines neuen Bezugssystems. Die Sonne wird den Fixsternen gleichgestellt.

Die Erde dreht sich während der Dauer eines Sterntages einmal gleichförmig um ihre Achse.

Diese Feststellung bringt die entscheidende Vereinfachung gegenüber der Beschreibung im geozentrischen Weltbild. Die Drehung eines Körpers (der Erde) genügt, um die scheinbare Rotation aller Fixsterne, der Sonne und der Planeten zu erklären. Die Himmelsachse ist damit die Drehachse der Erde.

Die Erde bewegt sich (zusätzlich zu ihrer Achsendrehung) während der Dauer eines Jahres einmal auf einer Kreisbahn um die Sonne.

Die Abbildung 2.10 zeigt, wie dadurch für einen Beobachter auf der Erde eine Verschiebung der Sonne entlang der Ekliptik zustande kommt.

2.10  Bewegung der Erde um die als ruhend angenommene Sonne und scheinbare Bewegung der Sonne entlang des Tierkreisgürtels.
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 254)

Dieser Beobachter projiziert die Sonne auf den (im Vergleich zur Entfernung Erde–Sonne) sehr weit entfernten Fixsternhintergrund. Während die Erde in den Stellungen 0, 1, 2, 3, ... 11 steht, erscheint die Sonne auf dem Fixsternhintergrund in den Punkten 0', 1', 2', 3', ... 11'. Die Projektion der Sonne beschreibt also eine Kreisbahn während der Dauer eines Erdumlaufes um die Sonne im Umlaufsinn der Erde (vgl. Animation 2.11).

2.11  Projektion der Sonne auf den Fixsternhintergrund (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

Die Schiefe der Ekliptik ist die Neigung der Bahnebene der Erde gegen den Erdäquator (Himmelsäquator). Die Rotationsachse der Erde schließt mit der Bahnebene (Ebene der Ekliptik) einen Winkel von 90° − 23°27' = 66°33' ein. Auf dieser Neigung der Erdachse gegen die Ekliptik beruht die Entstehung der Jahreszeiten (diese Erklärung gelang Kopernikus noch nicht). Am 21. 3. steht die Projektion der Sonne im Frühlingspunkt (F in der obigen Abbildung). Der beleuchtete Teil der Erde ist vom Körperschatten (annähernd) durch einen Meridian getrennt, während einer Umdrehung der Erde ist jeder Punkt ihrer Oberfläche ebenso lang im beleuchteten Teil wie im Schattenteil, es herrscht an jedem Ort der Erde Tag- und Nachtgleiche (Frühlingsbeginn auf der Nordhalbkugel). In der Stellung der Erde am 21. 6. (1 / 4 Jahr später) reicht der beleuchtete Teil der Erde nur bis zum südlichen Polarkreis, alle Orte südlich davon haben ständig Nacht (Polarnacht). Am nördlichen Wendekreis (23°27' n. Br.) steht die Sonne zu Mittag im Zenit. Alle Orte der nördlichen Halbkugel haben nun den längsten Tag und die kürzeste Nacht, nördlich des nördlichen Polarkreises geht die Sonne nicht unter, diese Kugelkappe befindet sich während der Erdrotation ständig im beleuchteten Teil der Erde. Diese lange Bestrahlungsdauer bewirkt (zusammen mit dem nördlich des nördlichen Wendekreises nun steilsten Einfall des Sonnenlichtes) eine starke Erwärmung der nördlichen Halbkugel (Sommerbeginn). Auf der südlichen Halbkugel herrschen entgegengesetzte Verhältnisse (kürzester Tag, längste Nacht, geringste Mittagshöhe der Sonne), es erfolgt geringste Erwärmung (Winterbeginn).

Alle Planeten bewegen sich so wie die Erde in Kreisbahnen um die Sonne.

Die Abbildung 2.12 zeigt, wie damit die komplizierten Bahnen der Planeten bezüglich des Fixsternhimmels als Projektionserscheinungen zu verstehen sind.

2.12  Bewegung eines äußeren Planeten gegen den Fixsternhintergrund als Projektionserscheinung.
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 254)

In der Abbildung 2.12 ist angenommen, dass ein Planet eine größere Entfernung von der Sonne hat als die Erde (äußerer Planet) und dass seine Umlaufzeit wesentlich größer ist als die der Erde. Während die Erde die Stellungen 0, 1, 2, 3, ... 11 einnimmt, ist der Planet in den Stellungen 0', 1', 2', 3', ... 11'. Seine Projektion auf den Fixsternhimmel erscheint an den Stellen 0'', 1'', 2'', 3'', ... 11''. In der Animation 2.13 ist eine solche Bewegung dargestellt.

2.13  Retrograde Bewegung eines Planeten im heliozentrischen Weltbild

Der Mond ist ein Satellit der Erde. Er bewegt sich auf einer Kreisbahn um die Erde.

Die Abbildung 2.14 zeigt einen Teil der Erdbahn und die Mondbahn für einige Stellungen der Erde.

2.14  Siderische und synodische Mondperiode
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 255)

Hat in der Stellung 1 der Erde der Mond die Stellung 1a, so ist Neumond. Es muss dabei keine Sonnenfinsternis eintreten, da die Mondbahnebene gegen die Erdbahnebene unter 5°9' geneigt ist (vgl. Abbildung 2.15, Erde in Stellung 1, Mond in Stellung 1a). Während die Erde von der Stellung 1 in die Stellung 2 gewandert ist, hat der Mond einen vollen Umlauf ausgeführt und erscheint nun an derselben Stelle des Fixsternhimmels. Die Dauer dieses Umlaufes heißt siderische Periodendauer. Eine siderische Mondperiode dauert 27,321662 Tage. Neumond tritt nach Abbildung 2.13 erst wieder ein, wenn die Erde in der Stellung 3 ist. Die Zeit zwischen zwei gleichen Mondphasen ist um etwa 2 Tage länger als die Umlaufzeit des Mondes um die Erde und heißt eine synodische Mondperiode (29,530575 Tage).

2.15  Erdbahn und Mondbahn
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 255)

Die Abbildung 2.15 zeigt, dass eine Sonnen- oder Mondesfinsternis nur möglich ist, wenn Neumond bzw. Vollmond eintritt, während die Erde nahe den Stellungen 2 oder 4 ist. Bei unveränderlicher Lage der Bahnebene des Mondes könnte das immer nur zu ganz bestimmten Tagen des Jahres vorkommen. Das ist aber nicht der Fall. Die Normale zur Mondbahnebene führt (wie die Achse eines Kreisels) eine Präzessionsbewegung auf einem Kegelmantel aus. Die Periodendauer dieser Präzession beträgt 18,6 Jahre.

3. Die Keplerschen Gesetze – Teil 1

Im kopernikanischen System müsste die Projektion der Sonne auf den Fixsternhintergrund die Ekliptik gleichmäßig schnell durchlaufen, wenn die Erde auf einer Kreisbahn gleichförmig um die Sonne als Mittelpunkt rotiert (vgl. Abbildung 2.10). Tatsächlich bewegt sich die Sonne gegen den Fixsternhintergrund im Laufe eines Jahres verschieden schnell. Dies ist alleine schon daraus ersichtlich, dass in einem Jahr mit 365 Tagen zwischen dem Durchlaufen des Frühlingspunktes (21. 3.) und Herbstpunktes (23. 9) 186 Tage vergehen. Kopernikus nahm zur Erklärung dieses Sachverhaltes an, dass die Erde und die Planeten zwar Kreisbahnen beschreiben, dass die Mittelpunkte dieser Kreisbahnen jedoch etwas außerhalb der Sonne liegen. Aber auch diese exzentrischen Kreisbahnen ergaben keine volle Übereinstimmung mit den Beobachtungen. Erst Johannes Kepler konnte zeigen, dass nur die Annahme elliptischer Planetenbahnen zur vollen Übereinstimmung mit den Beobachtungsdaten führt.

3.1  Johannes Kepler (1571 – 1630) (Quelle: Österreichische Nationalbibliothek, Public Domain Mark 1.0, https://jenikirbyhistory.getarchive.net/media/ kepler-johannes-3e1c10, 15.03.2022)

3.2  Tycho (de) Brahe (1546 – 1601) (Quelle: Line engraving after T. Gemperlin 1586, Creative Commons Attribution 4.0, https://www.lookandlearn.com/history-images/YW000744V/ Tycho-Brahe, 15.03.2022)

Kepler standen langjährige Beobachtungsreihen der genauen Planetenpositionen zur Verfügung, die Tycho Brahe und seine Assistenten aufgenommen hatten. Die Bahn des Planeten Mars bereitete Kepler zwar die größten Schwierigkeiten, sie erwies sich aber als besonders hilfreich, um die wahre Natur der Planetenbahnen aufzuklären. Nach jedem vollen Umlauf des Mars, der 687 Tage (dies ist seine siderische Umlaufzeit) dauert, befindet er sich wieder an der gleichen Stelle seiner Bahn. Die Erde hingegen nimmt zu diesen Zeiten verschiedene Positionen auf ihrer Umlaufbahn ein (vgl. Abbildung 3.3).

3.3  Erde und Mars

Mittels Triangulation gelang es Kepler, zunächst die Eigenschaften der Erdbahn zu ermitteln und die Bahnellipse der Erde mit all ihren Parametern zu bestimmen. Dazu gehören die Exzentrizität, der größte und der kleinste Abstand von der Sonne (das Aphel und das Perihel) sowie die Lage der Apsidenlinie, die durch diese beiden Bahnpunkte geht. Nach der Charakterisierung der Erdbahn konnte Kepler auch die Umlaufbahn des Mars bestimmen, indem er nun die Triangulation für verschiedene Punkte der Marsbahn ausführte. Für diese kamen noch weitere Bahnelemente hinzu: ihre Neigung gegenüber der Erdbahnebene und die Schnittlinie beider Ebenen, die durch einen aufsteigenden und einen absteigenden Knoten auf der Bahn definiert ist. Alle Abstände gab er als Verhältniswerte zur großen Halbachse der Erde an. Auf diese Weise ließ sich schließlich eine Landkarte des Sonnensystems mit den Bahnen aller Planeten erstellen, wenn auch nur im relativen Maßstab. Kepler fasste seine Erkenntnisse in den 3 Keplerschen Gesetzen zusammen.

Die Bahnen der Planeten sind Ellipsen, in deren einem gemeinsamen Brennpunkt die Sonne steht.

3.4  Das 1. Keplersche Gesetz

Unter den Bahnen der Planeten in unserem Sonnensystem hat die Bahn der Venus mit 0,00677 die geringste numerische Exzentrizität (ist also am kreisähnlichsten) und die Bahn des Merkurs mit 0,20563 die größte. Die numerische Exzentrizität der Erdbahn beträgt 0,01671. Dabei verstehen wir unter der numerischen Exzentrizität ε einer Ellipse das Verhältnis der Brennweite e (Abstand eines Brennpunktes vom Mittelpunkt) zur großen Halbachse a (Abstand eines Hauptscheitels vom Mittelpunkt).
Die Abbildung 3.5 zeigt die Bahnellipsen der Erde und des Merkur maßstabsgetreu vom nördlichen Ekliptikpol aus gesehen. Die Planeten laufen dabei gegen den Uhrzeigersinn. Der gelbe Punkt markiert die Sonne. Bei beiden Bahnen sind der zweite Brennpunkt und das Perihel eingezeichnet. In dieser Abbildung unterscheidet sich die Bahn der Erde von einem Kreis nur und ca. die Linienbreite der gezeichneten Ellipse.

3.5  Erde und Merkur

Die Tabelle 3.6 enthält die wesentlichen Bahndaten der Erde.

3.6  Bahndaten der Erde

Die Erde bewegt sich auf ihrer Bahn rechtläufig, d.h. vom Polarstern aus betrachtet gegen den Uhrzeigersinn. Die Erdbahn wird in guter Näherung durch eine Ellipse mit der Sonne in einem der beiden Brennpunkte beschrieben. Diese Ellipse weicht nur sehr wenig von einer Kreisbahn ab und erscheint für das bloße Auge wie ein etwas aus dem Mittelpunkt verschobener Kreis. Der größte und der kleinste Sonnenabstand weichen vom mittleren Sonnenabstand nur um ca. 1,67 % ab. Die Erde bewegt sich pro Tag ca. 2,57 Millionen km auf ihrer Bahn, das sind etwa 202 Erddurchmesser. In einer Sekunde überstreicht die Strecke Erde–Sonne eine Fläche von über 2 Milliarden km².
Da die Erde einen massereichen Mond besitzt, bewegt sich nicht wie bei mondlosen Planeten ihr Mittelpunkt auf der Keplerellipse um die Sonne, sondern der gemeinsame Schwerpunkt von Mond und Erde (das Baryzentrum des Erde-Mond-Systems). Dieser Schwerpunkt liegt zwar noch im Erdinneren, ist jedoch im Mittel etwa 4670 km vom Erdmittelpunkt entfernt. Der Erdmittelpunkt selbst kreist um den Schwerpunkt und beschreibt daher eine Schlangenlinie entlang der Ellipsenbahn mit ca. einer Schwingung pro Monat. In den Animationen 3.7 und 3.8 ist diese Bewegung qualitativ, d.h. nicht maßstabsgetreu dargestellt.

3.7  Erde und Mond

3.8  "Schlangenbewegung" des Erdmittelpunktes

Die Apsidenlinie (also die Verbindungslinie zwischen Perihel und Aphel) beschreibt die Ausrichtung der Erdbahnellipse innerhalb der Bahnebene. Der Erdmittelpunkt hingegen hat wegen der mondbedingten von der gleichmäßigen Ellipse leicht abweichenden welligen Bahnform sein eigenes Perihel. Dieses Erdmittelpunkts–Perihel liegt von Jahr zu Jahr je nach der aktuellen Mondstellung an einer etwas anderen Stelle der Bahn. Der Erdmittelpunkt passiert daher sein eigenes Perihel in deutlich unregelmäßigeren Abständen, in der Regel zwischen dem 3. und 4. Jänner. Gravitationseinflüsse der anderen Planeten üben Störungen auf die Erdbahn aus, welche deren Form und Lage geringfügig aber kontinuierlich ändern. Auch haben relativistische Effekte einen Einfluss. Infolgedessen dreht sich die Apsidenlinie langsam in der Bahnebene, und zwar in derselben Richtung, in der die Erde die Bahn durchläuft (rechtläufig). Diese sogenannte Periheldrehung beträgt siderisch 0,323° pro Jahrhundert. Infolgedessen wandert das Perihel in etwa 111500 Jahren einmal bezüglich des Fixsternhintergrunds rund um die Sonne. In der Animation 3.9 ist dieser Effekt stark übertrieben dargestellt.

3.9  Drehung der Apsidenlinie (Periheldrehung)

Der von der Sonne nach einem Planeten gezogene Radiusvektor überstreicht in gleichen Zeiten gleiche Flächen (Flächensatz).

3.10  Das 2. Keplersche Gesetz

In der Animation 3.10 sind die beiden "Ellipsensektoren" genau dann flächengleich, wenn die zugehörigen Ellipsenbögen vom Planeten in der gleichen Zeit durchlaufen werden, d.h.

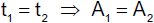
Die Quadrate der Umlaufszeiten zweier Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen ihrer Bahnellipsen.

3.11  Das 3. Keplersche Gesetz

Bezeichnet T₁ bzw. T₂ die Umlaufzeiten zweier Planeten und a₁ bzw. a₂ die großen Halbachsen ihrer Bahnellipsen (vgl. Animation 3.11), so gilt

Die Animation 3.12 zeigt die Bahnen der 5 sonnennächsten Planeten maßstabsgetreu und ihre Bewegung im Laufe eines Erdenjahres. Dabei "starten" die Planeten entlang einer Geraden. Die relativen Entfernungen aller 8 Planeten zur Sonne zeigt die Abbildung 3.13.

3.12  Das 3. Keplersche Gesetz

3.13  Das Sonnensystem

Johannes Kepler hat seine Gesetze rein empirisch (aus Beobachtungen) gefunden, konnte jedoch für sie keine Begründung mit Hilfe einer geeigneten Mechanik angeben. Die Anerkennung des kopernikanischen Systems stieß daher auf große Schwierigkeiten und es wurden zahlreiche Argumente gegen das neue System vorgebracht: Es war nicht einzusehen, durch welche Kraft die Planeten (vor allem die Erde, an der man doch eine solche Kraft hätte irgendwo merken müssen) um die Sonne bewegt werden; es wurde behauptet, dass mit der Erde nicht fest verbundenen Körper (z.B. die Luft) bei ihrer schnellen Bewegung um die Sonne (rund 30 km/s) abgestreift werden müssten. Schließlich glaubte die Kirche, im Verlust der zentralen Stellung der Erde einen Angriff gegen ihre Glaubenslehren sehen zu müssen.

3.14  Galileo Galilei (1564 – 1642)
(Quelle: "This image is taken from Page 30 of Memorials of Galileo Galilei, 1564-1642: Portraits and paintings, medals and medallions,
busts and statues, monuments and mural inscriptions" by Medical Heritage Library, Inc. is marked with CC BY-NC-SA 2.0.
https://wordpress.org/openverse/image/596855f2-5e07-4d93-9541-10dd3ebf7703, 18.03.2022)

Galileo Galilei war einer der eifrigste Verfechter des neuen Systems. Er baute ein leistungsfähiges Fernrohr (der Erfinder ist unbekannt) und konnte damit eine Reihe neuer Beobachtungen machen, die zur Stützung des kopernikanischen Systems geeignet waren. In diesem Fernrohr erschienen die Planeten als kleine Scheiben, während alle Fixsterne (auch bei stärkster Vergrößerung) als Punkte erschienen; daraus ergab sich der im Vergleich zum Abstand der Fixsterne sehr geringe Abstand der Planeten. Aus der erstmaligen Beobachtung, der Venusphasen (ähnlich den Mondphasen) konnte Galilei erkennen, dass die Planeten von der Sonne beleuchtet werden (wie der Mond) und nicht selbstleuchtende Körper sind (wie die Fixsterne). Galilei konnte erstmals beobachten, dass der Jupiter von mehreren Jupitermonden umkreist wird und damit ein Planetensystem im Kleinen darstellt. Aus der Beobachtung der Sonnenflecken konnte Galilei auf eine Achsendrehung der Sonne schließen. Er entdeckte Unebenheiten auf der Mondoberfläche; das stand im Gegensatz zur bisherigen Auffassung, dass die Himmelskörper ideale Kugelgestalt haben.
Trotz dieser Beobachtungen konnte Galilei seine gelehrte Mitwelt nicht überzeugen. Die Schwierigkeiten, gegen die er zu kämpfen hatte, spiegeln sich wohl am besten in seinen eigenen Worten:

"Als ich die Satelliten des Jupiter den Professoren von Florenz zeigen wollte, wollten sie weder diese noch das Teleskop sehen. Diese Leute glauben, es sei keine Wahrheit in der Natur zu finden, sondern nur in der Vergleichung von Texten."

Daraus wird deutlich, dass der Kampf Galileis nicht nur der Einführung des neuen kopernikanischen Systems galt, sondern ebenso einer der Naturwissenschaft angemessenen Methode der Erkenntnisgewinnung.

4. Das Gravitationsgesetz

4.1  Isaac Newton (1643 – 1727) (Quelle: https://ndla.no/subject:1:e0a0faa8-cefd-481f-bf79-b45ad4d7c5e7/ topic:3:182163/topic:3:166938/resource:1:166947, 19.03.2022)

4.2  Henry Cavendish (1731 – 1810) (Quelle: https://www.researchgate.net/figure/Sir-Henry-Cavendish-1731- 1810-outstanding-English-scientist_fig1_257847131, 19.03.2022)

Bis ins 16. Jahrhundert galten die Bahnen der Planeten einfach als Zeichen göttlichen Willens und göttlicher Ordnung. Nach dem von Isaac Newton als Grundgesetz der Mechanik erkannten Beharrungsgesetz (Trägheitsgesetz) kann sich jedoch kein Planet (so wie jeder andere Körper) ohne die ständige Wirkung einer Kraft auf einer krummen Bahn bewegen. Welche Kraft zwingt daher die Planeten in ihre fast kreisförmigen Bahnen? Die Idee, dass sich die Schwere nicht auf die Erde oder ihre nahe Umgebung beschränkt, sondern eine allgemeine Eigenschaft der Materie ist, also auch zwischen den Himmelskörpern wirksam sein könnte, ist bereits bei Kopernikus angedeutet und von Kepler ausgesprochen worden. Newton hat bereits im Jahr 1666 diesen Gedanken einer allgemeinen Gravitation geäußert und später (1684) nachgewiesen, dass die zwischen zwei Körpern wirksame Massenanziehung mit dem Quadrat der Entfernung abnimmt. Wir leiten das Gravitationsgesetz aus dem 3. Keplerschen Gesetz her.

Wenn 2 Planeten (Massen m₁ bzw. m₂) der Sonne Kreisbahnen mit den Radien r₁ bzw. r₂ in den Zeiten T₁ bzw. T₂ durchlaufen, so müssen auf sie die Zentripetalkräfte

bzw.

wirken. Nach dem 3. Keplerschen Gesetz gilt dann

Die Gravitationskraft ist also zum Quadrat der Entfernung indirekt proportional. Sie ist wie das Gewicht der Körper zur Masse des angezogenen Körpers direkt proportional. Wegen der Symmetrie jeder Wechselwirkung muss die zwischen 2 Körpern wirkende Gravitationskraft zur Masse jedes der beiden Körper proportional sein. Es gilt daher das folgende Newtonsche Gravitationsgesetz.

	Die zwischen 2 Massenpunkten mit den Massen m1 und m2 wirkenden Gravitationskräfte sind zum Quadrat ihrer Entfernung r indirekt proportional. Sie sind zur Masse jedes Massenpunktes direkt proportional. Die auf die beiden Massenpunkte wirkenden Kräfte haben denselben Betrag und zeigen jeweils auf den anderen Massenpunkt.

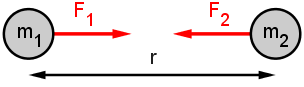
4.3  Gravitationsgesetz

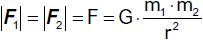	Der im Gesetz auftretende Proportionalitätsfaktor G heißt Gravitationskonstante.

Das Newtonsche Gravitationsgesetz beschreibt damit im Gegensatz zum mathematisch ähnlichen Coulombschen Gesetz (Kräfte zwischen zwei elektrischen Punktladungen) stets anziehende Kräfte. In vektorieller Form gilt für die auf den Massenpunkt m₁ wirkende Kraft

wobei r₁ und r₂ die Ortsvektoren der beiden Massenpunkte sind. F₂ zeigt auf den Massenpunkt m₁ und ist Gegenvektor zu F₁.

Wird der Massenpunkt m₁ von mehreren Massenpunkten m₂, m₃, ..., m_n angezogen, so addieren sich die einzelnen Kräfte zur auf den Massenpunkt m₁ wirkenden Gesamtkraft

Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. Da das Gravitationsgesetz linear in den Massen ist, kann der Körper gedanklich in kleine Teile zerlegt werden, deren Beiträge, wie oben vektoriell addiert werden können. Beim Grenzübergang zu "unendlich" kleinen Teilen ergibt sich statt einer Summe ein Integral. Es ergibt sich, dass eine homogene Kugel dieselbe Massenanziehung ausübt und erfährt wie die in ihrem Mittelpunkt vereinigte Gesamtmasse.

Die Bestimmung der Gravitationskonstanten G ist aus astronomischen Beobachtungen nicht möglich. Es müssten dazu für 2 Himmelskörper alle sonst im Gravitationsgesetz auftretenden Größen ermittelt werden. Im Laboratorium können die Massen m₁ und m₂ und der Zentralabstand kugelförmiger Körper leicht ermittelt werden. Es macht aber große Schwierigkeiten, die außerordentlich geringe Gravitationskraft zu messen. 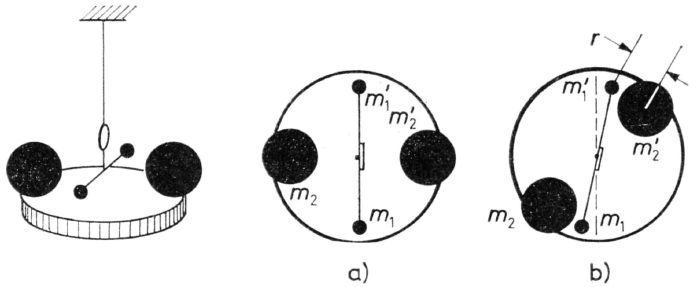Dies gelang erstmals Henry Cavendish im Jahr 1778 mit einer Drehwaage (vgl. Abbildung 4.4).

4.4  Drehwaage
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 260)

An einem dünnen Metallfaden hängt ein leichter Balken mit 2 gleichen Kugeln (Massen m₁ = m₁'). Ein an diesen Kugeln angreifendes Kräftepaar (Drehmoment) verdreht den Balken und kann aus dem sich einstellenden Drehwinkel (nach entsprechender Eichung) ermittelt werden. Dabei gilt analog zum Hookeschen Gesetz, dass der Drehwinkel zum angreifenden Drehmoment proportional ist. Während also eine gewöhnliche Federwaage auf Dehnung beansprucht wird, wird diese Drehwaage auf Torsion (Verdrillung) beansprucht. Der Drehwinkel wird mit einem am Metallfaden angebrachten Spiegel und einem Lichtzeiger festgestellt. Unter dieser Drehwaage befindet sich nun eine drehbare Scheibe mit zwei homogenen Kugeln möglichst großer Masse (m₂ = m₂'). Sind diese Kugeln in der Abbildung in der Stellung a), so wirkt am Waagbalken kein Drehmoment, er steht in der Nulllage. Dreht man nun die großen Kugeln in die Stellung b), so ergibt sich ein Ausschlag des Lichtzeigers infolge der Massenanziehung zwischen m₁ und m₂ sowie m₁' und m₂' (Kräftepaar). Die Animation 4.5 zeigt die Durchführung dieses Experiments.

4.5  Das Experiment von Cavendish

Aus diesem Ausschlag des Lichtzeigers ergibt sich die zwischen den Kugeln wirkende Gravitationskraft F. Der Abstand der Massenmittelpunkte und die Massen sind leicht messbar. Es kann daher die Gravitationskonstante G berechnet werden. Es gilt

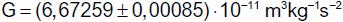
G gibt die Kraft an, die zwischen zwei Punktmassen von je 1 kg im Abstand 1 m wirkt. Sie ist außerordentlich klein. Nur Körper sehr großer Masse, wie etwa die Erde, bewirken eine deutlich merkbare Massenanziehung. Das Gravitationsgesetz enthält keinerlei Aussage über die Ursachen der Gravitation. Sie wird einfach als fundamentale Eigenschaft aller Materie beschrieben, ebenso wie die Trägheit eine solche Grundeigenschaft aller Körper ist.

Masse und Dichte der Erde

Das Gewicht F_G eines Körpers der Masse m auf der Erdoberfläche können wir auf zweierlei Weise ausdrücken:

Mit Hilfe der Erdbeschleunigung g

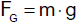
und mit Hilfe des Gravitationsgesetzes

Es muss daher

gelten. Daraus erhalten wir für die Masse der Erde

Nach Division durch das Erdvolumen

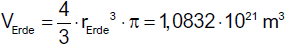
ergibt sich eine mittlere Dichte von ca.

Da die Bestandteile der Erdkruste nur eine mittlere Dichte von weniger als 3000 kg/m³ haben, müssen im Erdinneren Stoffe wesentlich größerer Dichte (Metalle) vorwiegen.

5. Das Gravitationsfeld einer Kugelmasse

Die Massenanziehung zwischen 2 Körpern ist als Wechselwirkung immer gegenseitig. Wenn wir einem der Körper eine zentrale Stellung einräumen (indem wir ihn z.B. als Bezugssystem verwenden), so sagen wir, dass er auf die Körper seiner Umgebung eine Gravitationskraft ausübt.

Den Raum, in dem die Gravitationskraft eines Körpers wirksam ist, nennen wir sein Gravitationsfeld.

Gemäß dem Gravitationsgesetz übt eine homogene Kugel der Masse M auf einen Massenpunkt m in der Entfernung r eine Gravitationskraft

aus. Der Massenpunkt m erfährt dadurch im Gravitationsfeld der Kugelmasse M eine Beschleunigung g.

5.1  Beschleunigung im Gravitationsfeld einer Kugelmasse M

bzw.

Diese Beschleunigung ist zum Mittelpunkt der Kugelmasse gerichtet. Sie entspricht der Kraft pro Masseneinheit und ist daher von m unabhängig. Sie hängt bei gegebener Masse M nur vom Ort ab und ist daher geeignet, die "Stärke" des Gravitationsfeldes an jedem Ort zu charakterisieren. Jedem Punkt des Gravitationsfeldes ist ein Beschleunigungsvektor g zugeordnet (vgl. Abbildung 5.2).

5.2  Beschleunigung im Gravitationsfeld einer Kugelmasse M

Wir definieren

	Unter der Feldstärke g des Gravitationsfeldes an irgendeiner Stelle verstehen wir die dort wirksame Gravitationskraft pro Masseneinheit.
	Gravitationsfeldstärke

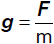Für die Gravitationsfeldstärke einer Kugelmasse M im Abstand r vom Mittelpunkt der Kugelmasse gilt

bzw.

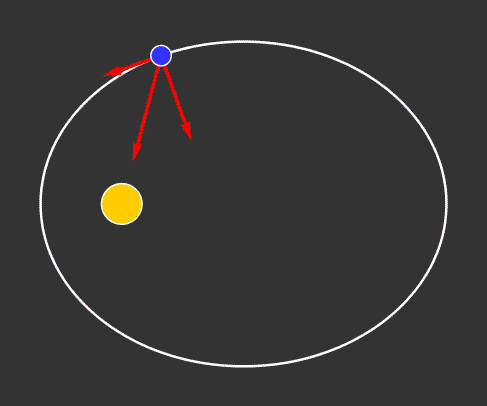
Die Animation 5.3 zeigt die Bewegung eines Planeten im Gravitationsfeld der Sonne. Die auf den Planeten wirkende Gravitationskraft zeigt stets zur Sonne und ist in eine zur Ellipsenbahn parallele bzw. normale Komponente zerlegt. Bei Annäherung an die Sonne bewirkt die Parallelkomponente eine Beschleunigung, bei Entfernung eine Abbremsung des Planeten. Im Perihel und im Aphel ist die Gravitationskraft normal zur Bahn und bewirkt daher nur eine Drehung.

5.3  Planetenbewegung unter dem Einfluss der Schwerkraft der Sonne

In der Abbildung 5.4 ist das Gravitationsfeld einer Kugelmasse M durch ein Feldlinienbild dargestellt. Die zum Zentrum weisenden Strahlen (Lote) geben die Richtung der Feldstärke an und heißen Feldlinien. Eine konzentrische Kugelschale wird überall mit gleicher Feldliniendichte durchsetzt; d.h. durch jeden m² dieser Kugelfläche treten gleich viele Feldlinien. Bei doppelt so groß gewähltem Kugelradius sinkt die Feldliniendichte auf den 4. Teil, da dieselbe Feldlinienzahl eine 4mal so große Fläche durchsetzt. Das bedeutet: Die Feldliniendichte ist ebenso wie der Betrag der Feldstärke zum Quadrat der Entfernung indirekt proportional, sie ist also zum Betrag der Feldstärke proportional. Die Gesamtzahl der von M ausgehenden Feldlinien ist dabei frei wählbar.

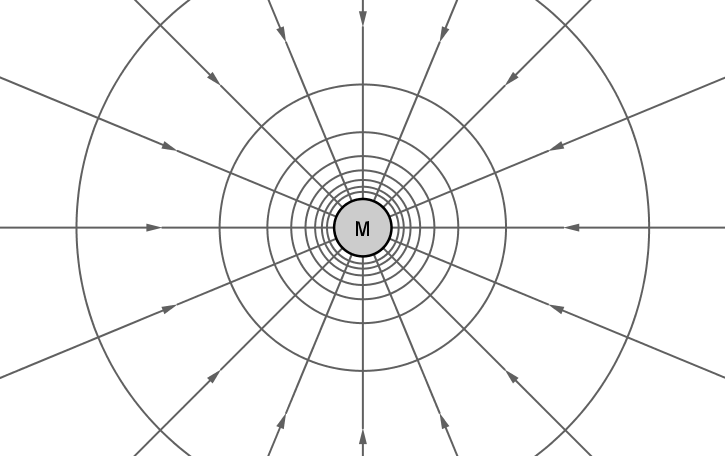
5.4  Feldlinienbild des Gravitationsfeldes einer Kugelmasse M

Das Gravitationsfeld kann durch ein Feldlinienbild dargestellt werden. Die Richtung der Feldlinien gibt die Richtung der Gravitationsfeldstärke (der Gravitationskraft) an, die Feldliniendichte ist zum Betrag der Feldstärke proportional.

Beim Heben eines Körpers im Gravitationsfeld der Erde muss Arbeit gegen die Schwerkraft verrichtet werden. In der Mechanik wird diese Hebearbeit nach der Formel W = G·h = m·g·h unter der Voraussetzung berechnet, dass die Erdbeschleunigung g (Gravitationsfeldstärke) bei geringem Höhenunterschied h konstant ist. In der Raumfahrt sollen jedoch Objekte in sehr große Entfernungen von der Erdoberfläche gebracht werden. Die Gravitationskraft kann dann nicht mehr als konstant angenommen werden (vgl. Animation 5.5).

5.5  Radiale Verschiebung eines Massenpunktes m im Gravitationsfeld einer Kugelmasse M

Im Folgenden soll die Arbeit W berechnet werden, die verrichtet wird, wenn ein Massenpunkt m im Gravitationsfeld einer Kugelmasse M aus dem Abstand r_A radial in den Abstand r_B > r_A verschoben wird. W ist durch die Fläche unter der "Kraftkurve" (Kraft-Weg-Diagramm) gegeben (vgl. Abbildung 5.6).

5.6  Gravitationskraft und Verschiebearbeit im Gravitationsfeld einer Kugelmasse M

Zur Berechnung der Verschiebearbeit teilen wir den Weg von r_A bis r_B durch die Punkte r₁, r₂, ..., r_n in n+1 gleiche Intervalle Δr. Wenn wir in jedem Intervall die Gravitationskraft durch irgendeinen in diesem Intervall vorkommenden konstanten Wert ersetzen (Treppenkurve), mit diesen konstanten Werten dann die Arbeit berechnen (Fläche der Rechteckstreifen) und schließlich die Wegintervalle Δr gegen Null streben lassen (n → ∞), erhalten wir die Arbeit entlang des Weges von r_A bis r_B. Betrachten wir nun das Wegintervall (r_k,r_k+1). Wegen r_k < r_k+1 gilt

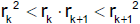
Für die Gravitationskraft in diesem Wegintervall folgt daraus

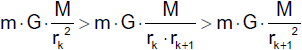
Als Näherungswert für die Verschiebearbeit in diesem Wegintervall erhalten wir

Daraus folgt als Näherungswert für die Gesamtarbeit

bzw.

da in dieser teleskopischen Summe alle Summanden bis auf die Randglieder wegfallen. Das Ergebnis ändert sich bei beliebig feiner Unterteilung des Weges nicht. Es gilt daher:

Um im Gravitationsfeld der Kugelmasse M den Massenpunkt m gegen die Gravitationskraft aus der Entfernung rA in radialer Richtung in die Entfernung rB > rA zu bringen, ist die Verschiebearbeit nötig. Diese Arbeit ist in erhöhter potentieller Energie des verschobenen Körpers gespeichert. Die Verschiebearbeit ist damit gleich der Differenz der potentiellen Energie am Anfangs- und Endpunkt der Verschiebung. Wird der Massenpunkt m aus der Entfernung rB > rA radial in die Entfernung rA verschoben, so wird potentielle Energie frei. Um den Massenpunkt m aus der Entfernung rA in unendlich große Entfernung zu bringen, ist die endliche Arbeit ("Fluchtenergie") nötig.

Wir haben bisher den Massenpunkt m in radialer Richtung vom Abstand r_A in den Abstand r_B verschoben. Nun soll der Massenpunkt aus einer Lage A in der Entfernung r_A auf beliebigem Weg s in irgendeine Lage B in der Entfernung r_B > r_A gebracht werden (vgl. Abbildung 5.7).

5.7  Wegunabhängigkeit der Verschiebearbeit

Wir können die Bewegung entlang des Weges s in der Abbildung durch eine radiale Verschiebung entlang des Weges r in die Lage C und weiter auf einer zur Kugelmasse M konzentrischen Kugelschale (Weg b) ersetzen. Zur Verschiebung auf der Kugelschale ist keine Arbeit nötig, da die Gravitationskraft keine Komponente in der Bewegungsrichtung hat; die potentielle Energie bleibt entlang jeder konzentrischen Kugelschale unverändert. Bringen wir den Massenpunkt m auf diesem Weg aus der Lage A in die Lage B, so ist dazu die durch obige Gleichung gegebene Arbeit nötig. Es gilt daher:

Um im Gravitationsfeld der Kugelmasse M einen Massenpunkt m aus der Entfernung rA in irgendeine Lage in der Entfernung rB zu bringen, ist entlang jedes Weges dieselbe Arbeit nötig. Die Größe W heißt potentielle Energie der Masse m bezüglich des Nullniveaus rA. Bewegung in einer zu M konzentrischen Kugelschale erfordert keine Arbeit und bewirkt keine Änderung der potentiellen Energie. Die zu M konzentrischen Kugelflächen heißen daher Äquipotentialflächen.

In der folgenden Abbildung 5.8 ist die Verschiebearbeit für eine Masseneinheit, also der Quotient

in Abhängigkeit vom Abstand r eingetragen.

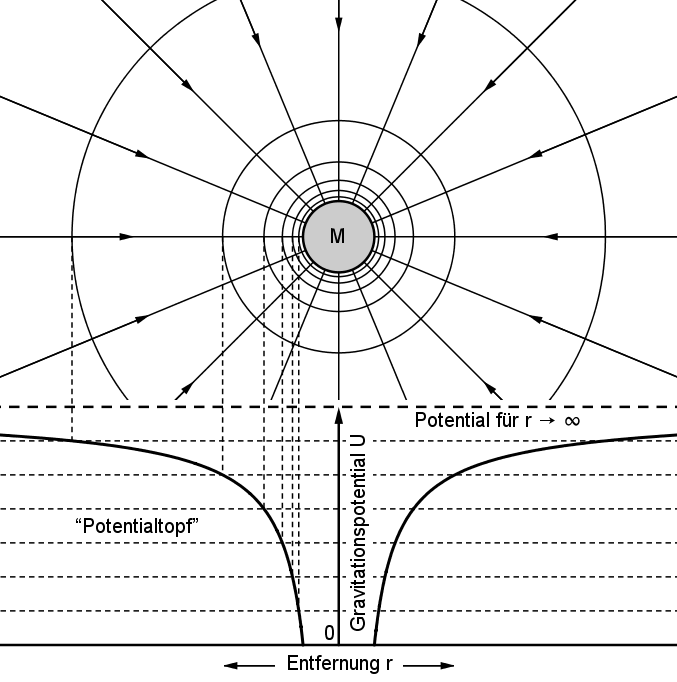
5.8  Potential einer Kugelmasse M

Als Nullniveau r₀ wurde die Oberfläche der Kugelmasse M gewählt. Wenn die Entfernung r gegen Unendlich strebt, strebt die Verschiebearbeit und damit die potentielle Energie gegen einen bestimmten Wert (Fluchtenergie). Die potentielle Energie pro Masseneinheit (also die Verschiebearbeit pro Masseneinheit) wird zweckmäßig zur Charakterisierung der potentiellen Energie in jedem Punkt um die Kugelmasse M verwendet. Wir definieren:

Die potentielle Energie pro Masseneinheit heißt das Potential U der Kugelmasse M im Abstand r bezüglich des Nullniveaus r0. Es ist Entlang jeder zur Kugelmasse M konzentrischen Kugelfläche herrscht konstantes Potential; solche Flächen konstanten Potentials heißen Äquipotentialflächen.

In der Abbildung ist eine Schar von Äquipotentialflächen eingezeichnet. Sie sind so gewählt, dass zwischen benachbarten Flächen gleiche Potentialdifferenz besteht. Man braucht also stets dieselbe Arbeit, wenn man einen Körper von einer dieser Flächen auf irgendeinem Weg bis zur nächsten Fläche befördert. Der von je 2 Äquipotentialflächen eingeschlossene Entfernungsunterschied wächst wegen des Absinkens der Gravitationskraft mit zunehmender Entfernung rasch an. Das bedeutet: Mit derselben Arbeit ΔW = m·ΔU kann man eine Masse m über jeden dieser Entfernungsabschnitte befördern.

Bemerkung: Das Nullniveau r₀ bezeichnet in der Physik einen Ort oder eine Fläche, auf den sich die Angabe der potentiellen Energie bezieht. Dort hat sie per definitionem den Wert Null. Diese Festlegung ist notwendig, da die potentielle Energie stets nur bis auf einen konstanten Betrag bekannt ist, der willkürlich festgelegt werden kann. Im Gravitationsfeld ist es üblich, das Nullniveau im Unendlichen anzusetzen. Dies ist möglich, weil das Gravitationspotential für sehr große Entfernung konvergiert (1/r₀ → 0 für r₀ → ∞). Da die Arbeit, die man aufwenden muss, um einen Körper aus dem Feld zu entfernen, in diesem Fall stets positiv ist, ist die potentielle Energie negativ. Es gilt dann

bzw.

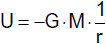6. Die Keplerschen Gesetze – Teil 2

Johannes Kepler hat seine Gesetze rein aus Beobachtungsdaten erschlossen. Nun soll gezeigt werden, dass sich die ersten beiden Gesetze auch mechanisch begründen lassen. Die Übereinstimmung des dritten Gesetzes mit dem Gravitationsgesetz wurde bei dessen Herleitung gezeigt.

Kegelschnitte in Polarkoordinaten

Wir betrachten in einem kartesischen Koordinatensystem eine Ellipse in 1. Hauptlage (vgl. Abbildung 6.1).

6.1  Ellipse in 1. Hauptlage

Ihre Gleichung in kartesischen Koordinaten ist durch

mit

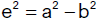
gegeben. Verschieben wir den Koordinatenursprung in den rechten Brennpunkt (e|0), so ergibt sich für die Ellipsengleichung

Zur Darstellung in Polarkoordinaten (vgl. Abbildung 6.2) setzen wir

bzw.

6.2  Kartesische Koordinaten und Polarkoordinaten

Einsetzen ergibt

Das ist eine quadratische Gleichung in r mit den Lösungen

Damit r positiv wird, wählen wir das positive Vorzeichen. Dann können wir kürzen und erhalten schließlich

Setzen wir

und

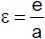dann vereinfacht sich die Polarkoordinatendarstellung zu

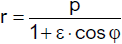
Die dimensionslose Größe ε heißt numerische Exzentrizität. In analoger Weise ergibt sich

für die Darstellung mit dem linken Brennpunkt im Koordinatenursprung. Dieselbe Darstellung, nämlich

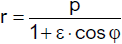
ergibt sich für alle Kegelschnitte, wobei die Art des Kegelschnitts von ε abhängt. Es gilt

Die Beschreibung der Dynamik eines Massenpunktes in einem Koordinatensystem

Die Dynamik eines Massenpunktes in Raum und Zeit wird in einem kartesischen Koordinatensystem durch eine Bahnkurve

beschrieben (vgl. Animation 6.3).

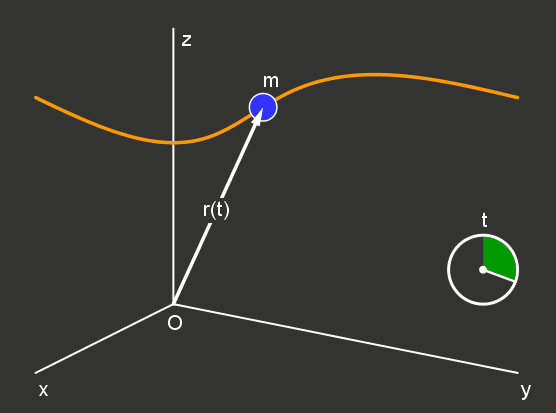
6.3  Bahnkurve eines Massenpunktes

Im Folgenden geben wir aus Gründen der Übersichtlichkeit der Schreibweise bei zeitabhängigen Funktionen das Funktionsargument t nicht an, wenn keine Mehrdeutigkeit gegeben ist. Die Geschwindigkeit v und die Beschleunigung a sind als Ableitungen nach der Zeit t definiert, sodass wir für Ort, Geschwindigkeit und Beschleunigung

erhalten. Da in der theoretischen Mechanik viele Probleme auf ein Zentralkraftproblem zurückgeführt werden können (wie auch die Bewegung eines Planeten im Gravitationsfeld der Sonne), ist es in diesen Fällen sinnvoll, in ein anderes Koordinatensystem zu wechseln. Die folgende Abbildung 6.4 zeigt ein Zylinderkoordinatensystem.

6.4  Zylinderkoordinaten

Die kartesischen Koordinaten transformieren sich in Zylinderkoordinaten wie folgt.

In diesen neuen Koordinaten sind Ort, Geschwindigkeit und Beschleunigung durch

gegeben. Erfolgt die Bewegung in der x-y-Ebene, so gilt wegen z = 0 und ρ = r

Das 1. Keplersche Gesetz

Die Umlaufbahn eines Trabanten ist eine Ellipse. Einer ihrer Brennpunkte liegt im Schwerezentrum des Systems.

Dieses Gesetz ergibt sich aus Newtons Gravitationsgesetz, sofern die Masse des Zentralkörpers wesentlich größer als die des Trabanten ist, die Wirkung des Trabanten auf den Zentralkörper vernachlässigt werden kann und keine Störungen durch andere Trabanten vorhanden sind.

Die Energie E für einen Trabanten mit Masse m im Newtonschen Gravitationsfeld des Zentralkörpers mit Masse M ist gegeben durch

Der Drehimpuls ist durch

gegeben. Für die zeitliche Änderung des Drehimpulses gilt

da die Wirkungslinie einer Zentralkraft und damit die Beschleunigung zu r parallel sind. Damit ist der Drehimpuls L konstant und die Bahn des Trabanten liegt in einer zu L normalen Ebene. Wir wählen unser Koordinatensystem so, dass die Bahn in der x-y-Ebene zu liegen kommt und sich der Zentralkörper im Ursprung des Koordinatensystems befindet. Wir drücken die Energie in Zylinderkoordinaten aus und erhalten für die kinetische Energie

bzw. für die Gesamtenergie

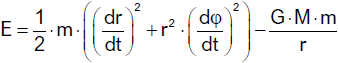
Der Drehimpuls L besitzt als einzige von Null verschiedene Komponente die z-Komponente und es gilt

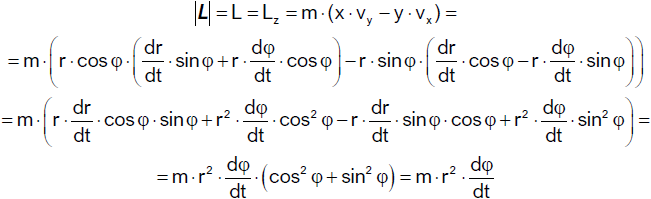
Aus der Formel für den Drehimpuls folgt

Damit und mit der Beziehung

lässt sich die Energiegleichung umformen.

Diese Differentialgleichung vergleichen wir mit der Polarkoordinatendarstellung eines Kegelschnittes.

Differenzieren ergibt

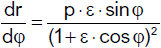
Alle Ausdrücke, die φ enthalten, werden durch Einsetzen der zu

umgeformten Gleichung der Bahnkurve eliminiert. Damit erhalten wir

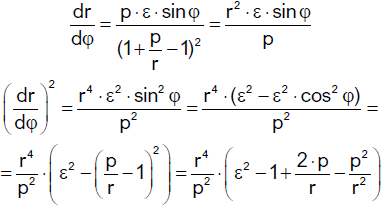
Durch Vergleich der Koeffizienten nach Potenzen von r in den Gleichungen

erhalten wir

und

Diese Lösung hängt nur von der spezifischen Energie E/m und dem spezifischen Bahndrehimpuls L/m ab. Der Parameter p und die numerische Exzentrizität ε bestimmen die Gestalt der Bahn (Art des Kegelschnittes). Für den Fall 0 < ε < 1 (E < 0) ist die Bahnkurve eine Ellipse mit einem Brennpunkt im Koordinatenursprung.

Legt man kein zentralsymmetrisches Kraftfeld zugrunde, sondern wechselseitig wirkende Gravitation, so bilden sich ebenfalls Ellipsenbahnen. Es bewegen sich aber beide Körper, das Zentrum der Umlaufbahnen ist der gemeinsame Schwerpunkt (Baryzentrum) von "Zentralkörper" und Trabant, als fiktive Zentralmasse ist die Gesamtmasse des Systems anzunehmen. Die Animation 6.5 zeigt ein "Doppelsternsystem". Das Massenverhältnis der beiden Körper beträgt 2:1.

6.5  Doppelsternsystem

Auch die Sonne "ruht" nicht im Sonnensystem. Obwohl die Sonne 99,86 Prozent der Gesamtmasse des Sonnensystems besitzt, liegt das Baryzentrum nicht immer innerhalb der Sonne. Seine Lage hängt vor allem von der Stellung des Jupiters und des Saturns zueinander ab. Diese beiden Planeten besitzen 0,10 bzw. 0,03 Prozent der Masse der Sonne, sodass sie das Baryzentrum um diesen Bruchteil ihrer Bahnhalbachsen beeinflussen (um ca. 740000 und 410000 km). Da der Sonnenradius 696.000 km beträgt, liegt das Baryzentrum mal innerhalb, mal außerhalb der Sonnenoberfläche, maximal 2,098 Sonnenradien vom Sonnenmittelpunkt entfernt, sodass auch die Sonne eine deutliche Bewegung zeigt (vgl. Abbildung 6.6).

6.6  Lage des Baryzentrums des Sonnensystems bezüglich der Sonne

Das 2. Keplersche Gesetz

In gleichen Zeiten überstreicht der Fahrstrahl Trabant–Schwerezentrum gleiche Flächen.

Unter dem Fahrstrahl verstehen wir die Verbindungslinie zwischen dem Schwerpunkt eines Trabanten und dem Gravitationszentrum, um das er sich bewegt.

Eine einfache Herleitung ergibt sich, wenn man die Flächen betrachtet, die der Fahrstrahl in kleinen Zeitabschnitten Δt zurücklegt und die Kraft als momentanen Kraftstoß nur jeweils am Ende eines Abschnitts einwirken lässt. Lässt man die Zeitschritte infinitesimal kleiner werden, so erhält man die Bahnbewegung bei kontinuierlich einwirkender Kraft.

6.7  Das 2. Keplersche Gesetz

In der Abbildung 6.7 ist Z das Kraftzentrum. Der Trabant bewegt sich im Zeitabschnitt Δt zunächst von A nach B. Würde sich seine Geschwindigkeit nicht ändern, so würde er sich im nächsten Zeitschritt Δt von B nach C bewegen. Da die beiden Dreiecke ZAB und ZBC die Seite ZB gemeinsam haben und zu dieser Seite auch eine gleich große Höhe (Projektion von AB bzw. BC auf die Normale zu ZB), beinhalten sie auch die gleiche Fläche. Wirkt nun im Punkt B eine Kraft in Richtung Z, so wird die Geschwindigkeit v um ein Δv abgelenkt, das parallel zur Strecke ZB ist. Statt bei C landet der Trabant also bei C'. Da auch die beiden Dreiecke ZBC und ZBC' dieselbe Basis und die gleiche Höhe haben, ist auch ihre Fläche gleich. Damit gilt der Flächensatz für die beiden kleinen Zeitabschnitte der Länge Δt und nach dem Grenzübergang Δt → 0 auch für die gekrümmte Bahnkurve.

Eine formelmäßige Herleitung geht von der in einem infinitesimalen Zeitschritt dt überstrichenen Fläche A aus. Diese Fläche ist gegeben durch (vgl. Abbildung 6.8)

6.8  Das 2. Keplersche Gesetz

Aus der Gleichung für den Drehimpuls

folgt (L ist konstant)

Die in einem beliebigen Zeitintervall (t₁,t₂) überstrichene Fläche ergibt sich durch Integration.

Für gleiche Zeitdifferenzen ist also die überstrichene Fläche gleich groß.

Kepler formulierte das Gesetz nur für den Umlauf der Planeten um die Sonne, es gilt aber auch auf nicht geschlossenen Bahnen. Das zweite Keplersche Gesetz ist im Gegensatz zu den anderen beiden Gesetzen nicht auf die 1/r²–Kraft der Gravitation beschränkt, sondern gilt allgemein für alle Zentralkräfte und Bewegungen mit konstantem Drehimpuls. Kepler war lediglich an einer Beschreibung der Planetenbahnen interessiert, doch ist das zweite Gesetz bereits die erste Formulierung des Gesetzes, das wir heute als Drehimpulserhaltung kennen.

7. Satelliten

Satelliten (lat. satelles "Begleiter, Leibwächter"), sind im erweiterten Sinne alle Objekte, die einen Himmelskörper "umkreisen". Künstliche Geräte, die die Erde umkreisen, werden speziell Erdsatelliten genannt. Man bezeichnet Flugkörper nur dann als Erdsatelliten, wenn sie die Erde im Weltraum umkreisen. Einem Satelliten fehlt nach Erreichen seiner Umlaufbahn ein Eigenantrieb, was ihn von einem Raumschiff unterscheidet. Einfache Bremsraketen, die z.B. zu einem kontrollierten Absturz führen, reichen nicht aus, einen Satelliten zum Raumschiff zu machen. Künstliche Satelliten, die einen anderen Körper als die Erde umlaufen, werden hingegen als Orbiter bezeichnet.

Ein Satellit in einer Kreisbahn

7.1  Satelliten in einer Kreisbahn um die Erde (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022, Icons erstellt von Freepik, https://www.flaticon.com/de/premium-icon/satellit_1891082, 01.04.2022)

Wenn sich ein Satellit auf einer Kreisbahn bewegt, so muss sich auch der "Zentralkörper" auf einer Kreisbahn bewegen. Dabei verhalten sich die Bahnradien umgekehrt wie die Massen der beiden Körper (vgl. Animation 7.2).

7.2  Bewegung zweier Körper auf Kreisbahnen um den Massenmittelpunkt

Der Abstand zwischen den beiden Körpern bleibt konstant und damit auch der Betrag der stets zum gemeinsamen Massenmittelpunkt weisenden Gravitationskraft. Wenn die Masse m des Satelliten gegen die Masse des "Zentralkörpers" vernachlässigbar klein ist, fällt der Massenmittelpunkt des Systems mit dem Massenmittelpunkt des Zentralkörpers zusammen, die Bewegung des Zentralkörpers kann vernachlässigt werden, er ruht also im Ursprung unseres Bezugssystems. Das ist bei den künstlichen Erdsatelliten der Fall; auch bei den Planeten der Sonne trifft dies annähernd zu. Wir beschränken uns auf diesen wichtigen Sonderfall.

7.3  Satellit in einer Kreisbahn

Damit sich ein Satellit der Masse m in einer Kreisbahn mit dem Radius r um den Mittelpunkt des Zentralkörpers der Masse M bewegt, muss auf ihn eine Zentripetalkraft

wirken (vgl. Abbildung 7.3). Diese Zentripetalkraft ist die Gravitationskraft

Es gilt daher die Gleichgewichtsbedingung

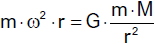
oder

oder

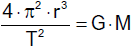
Für die Umlaufzeit T eines Satelliten erhalten wir somit

Die Umlaufzeit ist von der Masse des Satelliten unabhängig. Hat ein Zentralkörper mehrere Satelliten, so sind die Quadrate ihrer Umlaufzeiten zu den dritten Potenzen der Bahnradien proportional (3. Keplersches Gesetz). Damit ein Erdsatellit in eine Kreisbahn um die Erde gelangt, muss er also bei vorgegebener Höhe r in die Richtung der Kreistangente mit einer ganz bestimmten Geschwindigkeit v gelangen. Mit

ergibt sich

und somit für die Tangentialgeschwindigkeit v des Satelliten

Die Geschwindigkeit ist also umso kleiner, je größer der Bahnradius ist. Aus der Gleichung für die Umlaufzeit T ergibt sich eine Möglichkeit, aus den bekannten Daten (T, r) einer (kreisförmigen) Planetenbahn die Masse M des Zentralkörpers zu berechnen.

Da die Erdbahn fast kreisförmig ist, dürfen wir diese Gleichung zur Berechnung der Sonnenmasse anwenden und erhalten

Die Masse der Sonne beträgt somit ca. 333000 Erdmassen.

Wir wollen die Geschwindigkeit v₁ eines künstlichen Erdsatelliten in unmittelbarer Nähe der Erdoberfläche berechnen. Der Luftwiderstand soll vernachlässigt werden, der Bahnradius sei gleich dem Erdradius. Es muss dann die Zentripetalbeschleunigung

gleich der Erdbeschleunigung g sein. Damit gilt

und somit

Diese Geschwindigkeit heißt die 1. kosmische Geschwindigkeit. Mit dieser Geschwindigkeit müsste ein Körper an der Erdoberfläche horizontal abgeschossen werden, damit er in einer Kreisbahn entlang der Erdoberfläche verbleibt. Er benötigt dann für einen Erdumlauf die Zeit

Jeder andere Erdsatellit bewegt sich langsamer und benötigt eine größere Umlaufzeit. Soll ein Satellit über einem bestimmten Punkt des Äquators verharren (nur am Äquator ist das möglich), so muss seine Umlaufzeit mit der Dauer einer Achsendrehung der Erde (1 Sterntag = 86164 Sekunden) übereinstimmen (vgl. Animation 7.1). Für den Bahnradius eines solchen geostationären Satelliten ergibt sich

Das sind 35767 km über der Erdoberfläche.

Die Gesamtenergie eines Satelliten in einer Kreisbahn in der Höhe h = r − r₀ (r₀ = Erdradius) setzt sich aus seiner potentiellen Energie

und seiner kinetischen Energie

zusammen. Er hat daher bezüglich der Erdoberfläche die Gesamtenergie

Ein Satellit an der Erdoberfläche (r = r₀) hat die geringste Gesamtenergie

Er hat jedoch die größte Bewegungsenergie. Mit zunehmender Entfernung wächst die Gesamtenergie und strebt für r → ∞ gegen die Fluchtenergie

Um einen Satelliten (Körper) in beliebig große Entfernung von der Erdoberfläche zu bringen, muss seine Bewegungsenergie gleich der Fluchtenergie sein. Wir erhalten aus

für die 2. kosmische Geschwindigkeit (Fluchtgeschwindigkeit) v₂

Diese Geschwindigkeit reicht aus, um einen Körper an einen beliebigen Punkt des Weltraumes zu bringen. Von der Anziehung durch andere Himmelkörper wird dabei abgesehen.

Die möglichen Satellitenbahnen

Die Abbildung 7.4 zeigt die möglichen Satellitenbahnen.

7.4  Mögliche Bahnen eines im Punkt P horizontal abgeschossenen Satelliten
(Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

Bei horizontalem Abschuss mit der 1. kosmischen Geschwindigkeit ergibt sich eine Kreisbahn. Wird der Körper horizontal mit einer Geschwindigkeit abgeschossen, die über der 1. kosmischen Geschwindigkeit, aber unter der 2. kosmischen Geschwindigkeit liegt, so kann der Körper nur eine endliche Entfernung von der Erde erreichen, er bleibt ein Satellit der Erde. Gemäß dem 1. Keplerschen Gesetz ist die Bahn eine Ellipse mit einem Brennpunkt im Mittelpunkt der Erde. Mit wachsender Abschussgeschwindigkeit kann der Körper in immer größere Erdentfernung gelangen, die elliptische Bahnkurve wird stärker exzentrisch. Überschreitet die Abschussgeschwindigkeit die 2. kosmische Geschwindigkeit, so kann der Körper in beliebig große Erdentfernung gelangen. Seine Bahn muss offenbar wegen der immer schwächer werdenden Erdanziehung in eine Gerade übergehen. Er flüchtet auf einer Hyperbel ins Unendliche. Für v = v₂ würde sich eine Parabelbahn ergeben.

8. Die Achsendrehung der Erde

Die Corioliskraft

Die Corioliskraft (benannt nach dem französischen Physiker Gaspard Gustave de Coriolis, 1792 – 1843) ist eine der drei Trägheitskräfte der klassischen Mechanik, die in einem rotierenden Bezugssystem auftreten. Die Corioliskraft tritt genau dann in Erscheinung, wenn ein Körper sich in einem rotierenden Bezugssystem bewegt und wenn diese Bewegung nicht parallel zur Rotationsachse bzw. zum Vektor der Winkelgeschwindigkeit verläuft. Die beiden anderen Trägheitskräfte in einem rotierenden Bezugssystem, Zentrifugalkraft und Eulerkraft, wirken auch, wenn der Körper im rotierenden Bezugssystem ruht. Betrachten wir dazu das folgende Szenario.
Vom Mittelpunkt einer rotierenden Scheibe wird eine Kugel radial nach außen abgeschossen (vgl. Animation 8.1). Im ruhenden Bezugssystem (Inertialsystem) bewegt sich die Kugel nach dem Abschuss gleichförmig geradlinig; im rotierenden Bezugssystem (Scheibe) bewegt sich die Kugel auf einer gekrümmten Bahn.

8.1  Corioliskraft

Zur Berechnung der Corioliskraft betrachten wir die beiden Bezugssysteme S (das ruhende System) und S' (das rotierende System). Die Koordinatenursprünge beider Systeme sollen übereinstimmen, das System S' soll mit der Winkelgeschwindigkeit ω um eine Achse durch seinen Koordinatenursprung bezüglich des Systems S rotieren. Der Ort eines Massenpunktes ist im System S durch einen Ortsvektor r definiert, der durch drei Basisvektoren e_k und drei Koordinaten x_k dargestellt wird (k = 1,2,3).

Ist der Punkt beweglich, hängen die Koordinaten x_k von der Zeit ab. Die Zeitableitungen des Ortsvektors r sind

Sie geben die Geschwindigkeit bzw. Beschleunigung an, mit der sich der Massenpunkt relativ zum Bezugssystem S bewegt. Auf gleiche Weise ist der Ort des Massenpunktes bezüglich des Systems S' durch einen Ortsvektor r' mit entsprechenden Basisvektoren e'_k und Koordinaten x'_k festgelegt. Ort, Geschwindigkeit und Beschleunigung des Massenpunktes bezüglich des Systems S' sind gegeben durch

Damit die beiden Vektoren r und r' denselben physikalischen Ort im Raum definieren, muss

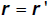
bzw.

gelten. Zur Transformation der Geschwindigkeit und Beschleunigung bilden wir die Zeitableitungen bezüglich des Systems S und beachten, dass die Basisvektoren des Systems S' vom System S aus gesehen nicht zeitlich konstant sind. Wir erhalten

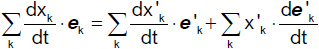
Die Änderungsgeschwindigkeit der Basisvektoren des Systems S' ist durch

gegeben. Daraus folgt

und auf analoge Weise

Für die Beschleunigung erhalten wir daher

Bewegt sich der Massenpunkt bezüglich des Systems S kräftefrei, d.h. a = 0, so gilt

Multiplikation mit der Masse m des Massenpunktes ergibt die im rotierenden System S' wirkende Trägheitskraft

Die Summanden auf der rechten Seite dieser Gleichung sind die Corioliskraft

die Eulerkraft

und die Zentrifugalkraft

Die Corioliskraft wirkt wie bereits oben erwähnt nur auf bewegte Körper. Sie ist zur Bewegungsrichtung stets normal und verrichtet daher keine Arbeit, sondern bewirkt nur eine Änderung der Bewegungsrichtung.

Die Ablenkung von Winden und Meeresströmungen

8.2  Die Ablenkung von Winden durch die Corioliskraft
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 263)

Horizontal bewegte Körper werden auf der nördlichen Halbkugel (in Bewegungsrichtung gesehen) nach rechts abgelenkt. Auf der südlichen Halbkugel erfolgt die Ablenkung nach links.
Die Winde verhalten sich ebenso wie die Kugel auf der rotierenden Scheibe. An den Polen der Erde herrschen offenbar dieselben Verhältnisse wie auf der rotierenden Scheibe, wenn wir uns eine nicht zu große Umgebung des Pols durch eine Ebene ersetzt denken (vgl. Abbildung 8.2). Wenn ein am Pol stehender Beobachter eine Kugel mit der Geschwindigkeit v radial von sich wegstößt, so verharrt sie bezüglich des Fixsternsystems (das ein Inertialsystem ist) in dieser Bewegung auf gerader Bahn; sie beschreibt bezüglich der Erde dann die in der Abbildung wiedergegebene Bahn. Unter der im Fixsternsystem sich nach dem Beharrungsgesetz geradlinig bewegenden Kugel dreht sich die Erde weg. Der Beobachter auf der Erde hat den Eindruck, dass auf die Kugel eine sie nach rechts ablenkende Kraft wirkt (die Corioliskraft). Die Ablenkung der Kugel von der geraden Bahn tritt beim Wegstoßen in jeder Richtung in gleicher Weise auf.
Für einen irdischen Beobachter in der geographischen Breite φ denken wir uns auch an diesem Ort die Erde durch einen kleinen Teil der Tangentialebene ersetzt. Für die in der Abbildung dargestellte Ablenkung ist nun die Drehung der Tangentialebene um eine zu ihr normale Achse maßgebend. Die an den Pol gelegte Tangentialebene rotiert mit der Winkelgeschwindigkeit ω der Erde. Für die in P gelegte Tangentialebene ist nur die dazu normale (also in der Drehachse durch P liegende) Komponente der Winkelgeschwindigkeit ω·sin φ maßgebend. Die Ablenkung verschwindet demnach am Äquator (sin φ= 0), sie ist am größten an den Polen (sin φ= ±1). Stets ist die Ablenkung von der Bewegungsrichtung unabhängig, sie tritt also bei Ost-West-Bewegungen ebenso auf wie bei Nord-Süd-Bewegungen.

8.3  Hoch- und Tiefdruckgebiet auf der Nordhalbkugel

8.4  Tiefdruckgebiet an der Südwestküste von Island
(Quelle: NASA/GSFC, MODIS Rapid Response Team, Jacques Descloitres, https://visibleearth.nasa.gov/images/68992/low-off-iceland, 13.04.2022)

8.5  Großräumige ozeanische Strömungen unter Beteiligung der Corioliskraft
(Quelle: U.S. National Oceanic and Atmospheric Administration, https://commons.wikimedia.org/wiki/File:Oceanic_gyres.png, 13.04.2022)

Der Foucaultsche Pendelversuch

8.6  Jean Bernard Léon Foucault (1819 – 1868); das Foucaultsche Pendel im Panthéon (Paris)
(Quelle: "File:Foucault portre crop.jpg" by Zátonyi Sándor, (ifj.) Fizped is marked with CC BY 3.0,
https://wordpress.org/openverse/image/70d663f2-a7a4-46bd-9fe4-dfdbd485f883, 10.04.2022,
"Foucault pendulum, Pantheon" by Andy Hay is marked with CC BY 2.0,
https://wordpress.org/openverse/image/61368d50-dd76-4101-998b-7a830d846497, 11.04.2022)

Ein Foucaultsches Pendel ist ein Fadenpendel (Kugel an einem dünnen Faden) mit großer Pendellänge und -masse, mit dessen Hilfe ohne astronomische Beobachtungen die Erdrotation nachgewiesen werden kann.
Wird ein Fadenpendel aus seiner Ruhelage ausgelenkt und dann losgelassen, so ist die treibende Komponente der Schwerkraft stets normal zum Pendelfaden und liegt in der durch den gespannten Faden und die Ruhelage bestimmten Ebene. Da niemals eine Kraftkomponente normal zu dieser Ebene auftritt, kann bezüglich eines Inertialsystems keine zu dieser Ebene normale Geschwindigkeitskomponente auftreten, die Schwingungsebene des Pendels bleibt dann bezüglich dieses Inertialsystems unverändert (vgl. Animation 8.7).

8.7  Fadenpendel

Im Jahr 1851 beobachtete der französische Physiker Léon Foucault bei einem Versuch, dass sich die Schwingungsebene eines Pendels langsam drehte. Die Schwerkraft, die nur senkrecht wirkt, konnte diese Drehung nicht verursachen, und keine weitere äußere Kraft wirkte auf das Pendel ein. Also war es nicht das Pendel, sondern der Boden (die Erde), der seine Richtung änderte. Am 26. März 1851 führte er diesen Versuch im Pariser Panthéon mit einem 67 Meter langen Pendel und einem 28 Kilogramm schweren Pendelkörper der Öffentlichkeit vor. Am unteren Ende des Pendelkörpers befand sich eine Spitze, die mit jeder Schwingung eine Spur in einem Sandbett auf dem Fußboden markierte. Dies war ein aufsehenerregender Nachweis der Erdrotation.
Denken wir uns ein solches Fadenpendel am Nordpol der Erde aufgestellt, so muss also seine Schwingungsebene bezüglich des Fixsternsystems (falls dieses ein Inertialsystem ist) unveränderte Orientierung behalten. Die Erde muss sich (falls sie sich tatsächlich gegen ein Inertialsystem dreht) gegenüber der Pendelebene verdrehen. Ein am Pol stehender Beobachter gewinnt den Eindruck, dass sich die Pendelebene bezüglich der Erde entgegen dem Sinne der Erddrehung dreht, und zwar während eines Sterntages um 360° (vgl. Abbildung 8.8).

8.8  Foucaultsches Pendel
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 264)

In der geographischen Breite φ ist wieder die in Abbildung 8.2 ersichtliche Komponente der Winkelgeschwindigkeit der Erde wirksam.

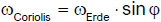
Als Beispiel betrachten wir ein am Wiener Stephansplatz aufgestelltes Pendel. Die Winkelgeschwindigkeit der Erddrehung beträgt

und die geographische Breite des Stephansplatzes ist

Damit erhalten wir

was einer Drehung der Schwingungsebene des Pendels um den Winkel

im Laufe eines Sterntages entspricht. Eine volle Umdrehung von 360° dauert daher ca. 32 Stunden.

Die Abplattung der Erde

Die im Laufe langer Zeit verformbare Erde müsste die Kugelgestalt als Gestalt kleinstmöglicher potentieller Energie annehmen, sie besitzt jedoch genähert die Form eines Rotationsellipsoids (vgl. Abbildung 8.9).

8.9  Die Abplattung der Erde

Die Abplattung zeigt das Auftreten einer zur Erdachse normalen Fliehkraft und damit die Rotation der Erde gegen ein Inertialsystem. Eine Oberfläche wird sich normal zu der aus Gravitationskraft und Fliehkraft gebildeten Resultierenden einstellen (vgl. Abbildung 8.10). Am Äquator beträgt das Gewicht eines 1 kg Stückes nur ca. 9,78 N, an den Polen beträgt es ca. 9,83 N.

8.10  Die Abplattung der Erde

Die Präzessionsbewegung der Erdachse

Die rotierende Erde ist ein Kreisel. Die Abplattung der Erde hat eine Präzessionsbewegung der Erdachse zur Folge (vgl. Abbildung 8.11)

8.11  Die Präzessionsbewegung der Erde
(Quelle: Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969, S. 264)

Wir denken uns die Erde in eine Kugel und einen entsprechenden Restkörper unterteilt. Wenn auch zwischen der insgesamt von der Sonne auf die Erde wirkenden Gravitationskraft und der Fliehkraft Gleichgewicht besteht, so gilt das nicht für jeden Teil der Erde. Für den der Sonne näher gelegenen Teil des Restkörpers ist die Gravitationskraft (sie nimmt mit geringerer Entfernung zu) größer als die Fliehkraft (sie ist bei geringerer Entfernung kleiner). Es verbleibt eine zur Sonne weisende Resultierende F₁. Umgekehrt ergibt sich an dem von der Sonne weiter entfernten Teil des Restkörpers eine von der Sonne wegweisende Resultierende F₂. Dieses Kräftepaar versucht, die Erdachse zu kippen; die Erde reagiert darauf als Kreisel mit einer Präzessionsbewegung. Die Erdachse durchläuft einen Kegelmantel in einer Zeit von etwa 25700 bis 25800 Jahren (1 Platonisches Jahr). Der Himmelspol wandert demnach am Fixsternhimmel in dieser Zeit entlang eines Kreises einmal herum (vgl. Abbildung 8.12). Ebenso wie die Gravitationskraft zwischen Erde und Sonne trägt auch die Gravitationskraft zwischen Erde und Mond zur Präzession bei.

8.12  Das Platonische Jahr
(Quelle: Erstellt mit Stellarium 0.21.3 - https://stellarium.org/de/, 20.04.2022)

9. Die Erde und ihr Mond

9.1  Der Mond
(Quelle: "Moon" by .Dwayne. is marked with CC BY-NC-ND 2.0,
https://wordpress.org/openverse/image/9894789b-fa61-41cd-be75-585258ce3810, 21.04.2022)

9.2  Maßstabgetreues Größen-Abstands-Verhältnis zwischen Erde und Mond

9.3  Der Mond in Zahlen

Der Erdmond ist der einzige natürliche Satellit der Erde. Er ist mit einem Durchmesser von 3476 km der fünftgrößte Mond des Sonnensystems und gemessen an der Größe seines Zentralkörpers (der Erde) der größte. Steht er am Himmel, so ist er ein sehr auffälliges "Gestirn". Deshalb prägte er zusammen mit der Sonne die Kalender der Menschen. Aufgrund seiner verhältnismäßigen Nähe zur Erde ist er der einzige fremde Himmelskörper, der bisher von Menschen betreten wurde und auch der am weitesten erforschte. Am 20. Juli 1969 betrat der Kommandant von Apollo 11, Neil Armstrong, als erster Mensch den Mond. Im Zeitraum von 1969 bis 1973 waren insgesamt 6 Landeversuche der US-Amerikaner erfolgreich. Die von den amerikanischen Astronauten mitgebrachten Gesteinsproben halfen, viel über den Mond zu erfahren. Von den Astronauten zurückgelassene Reflektoren werden noch heute dazu verwendet, die Distanz Erde - Mond auf Zentimeter genau zu bestimmen.
Nach heutiger mehrheitlich akzeptierter Vorstellung ist der Mond in der Frühzeit des Sonnensystems durch einen gewaltigen Einschlag auf der Erde entstanden. Die Proto-Erde, die damals bereits etwa 90 % ihrer heutigen Masse hatte, kollidierte vor ca. 4,5 Milliarden Jahren mit einem anderen etwa marsgroßen Proto-Planeten namens Theia. Theia selbst wurde bei dieser Kollision zerstört. Die Kollision erfolgte nicht frontal, sondern streifend, sodass große Materiemengen, bestehend aus Teilen des Mantels des Impaktkörpers und des Erdmantels, weggeschleudert und im Erdorbit eingefangen wurden. Aus den Trümmern der Kollision bildete sich in weniger als 100 Jahren der Proto-Mond, der rasch alle restlichen Trümmer einsammelte und sich nach knapp 10000 Jahren zum Mond mit annähernd heutiger Masse verdichtet haben muss. Er umkreiste die Erde damals in einem Abstand von nur rund 60000 km, was zu extremen Gezeitenkräften geführt haben muss, die Erde und Mond eiförmig deformierten. Aufgrund der extremen Reibung der bewegten flüssigen Gesteine führte das zu einer schnellen Abbremsung der Rotation um den gemeinsamen Schwerpunkt, worauf sich Erde und Mond voneinander entfernten. Die heutige Geschwindigkeit der Erdrotation ist demnach durch diese frühen Vorgänge beeinflusst.
Die Bahn des Mondes um die Erde weicht deutlich von der Kreisform ab. Die größte und die kleinste Entfernung zur Erde weichen im Mittel jeweils um 5,45 % von der Kreisform ab. Die Bahn ist in guter Näherung eine Ellipse der numerischen Exzentrizität 0,0549 und unter 5,15° gegen die Bahnebene der Erde (die Ekliptik) geneigt. Den erdnächsten Punkt der Bahn nennt man Perigäum. Im Perigäum beträgt die Entfernung im Mittel 363.300 km. Der erdfernste Punkt heißt Apogäum. Dort beträgt die Entfernung im Mittel 405.500 km.

9.4  Vollmond - der Unterschied zwischen einem Vollmond in Erdferne (rechts) und einem Vollmond in Erdnähe (links) beträgt
etwa zwölf Prozent im Durchmesser - so viel wie der Unterschied zwischen einer 1-Euro-Münze und einer 2-Euro-Münze.
(Quelle: Ernst Schindler, https://www.br.de/sternenhimmel/supermond-groesster-vollmond-mond-riesig-springfluten-100.html, 21.04.2022)

Der Mond umläuft zusammen mit der Erde die Sonne, durch die Bewegung um die Erde pendelt der Mond jedoch um eine gemeinsame Ellipsenbahn. Die Variation der Gravitation während dieser Pendelbewegung führt zusammen mit geringeren Störungen durch die anderen Planeten zu Abweichungen von einer exakten Keplerellipse um die Erde. Der erdnächste Punkt der Bahn wird nicht nach genau einem Umlauf (relativ zu den Fixsternen) des Mondes wieder erreicht. Durch diese Apsidendrehung umläuft das Perigäum die Erde in 8,85 Jahren.
Die mittlere Entfernung zwischen dem Mond und der Erde wächst jährlich um etwa 3,8 cm. Der Abstand wird seit der ersten Mondexpedition Apollo 11 regelmäßig vermessen, indem die Lichtlaufzeit bestimmt wird, die Laserlicht für die Strecke hin und zurück benötigt. Sowohl von amerikanischen als auch von sowjetischen Mondmissionen wurden dazu insgesamt fünf Reflektoren auf dem Mond platziert, die heute für die Entfernungsmessungen genutzt werden.
Die allmählich zunehmende Entfernung ist eine Folge der Gezeitenkräfte, die der Mond auf der Erde bewirkt. Dabei wird Rotationsenergie der Erde überwiegend in Wärme umgewandelt und zu einem Teil als Rotationsenergie auf den Mond übertragen. Der dabei abnehmende Drehimpuls der Erdrotation resultiert in einer Zunahme des Bahndrehimpulses des Mondes, der sich dadurch von der Erde entfernt. Dieser schon lange vermutete Effekt ist seit 1995 durch die Laser-Distanzmessungen abgesichert. Er bewirkt sowohl eine kontinuierliche Verlängerung der irdischen Tageslänge (um etwa eine Sekunde in 100000 Jahren) als auch der Mondumlaufdauer.
Infolge der Gezeitenwirkung, die durch die Gravitation der Erde entsteht, hat der Mond seine Rotation der Umlaufzeit in Form einer gebundenen Rotation angepasst. Das heißt, bei einem Umlauf um die Erde dreht er sich im gleichen Drehsinn genau einmal um die eigene Achse. Daher ist - abgesehen von kleineren Abweichungen, den Librationsbewegungen - von einem Punkt der Erdoberfläche immer dieselbe Mondseite zu sehen. Wegen der Libration und der Parallaxe, sprich durch Beobachtung von verschiedenen Punkten etwa bei Mondaufgang und Monduntergang, sind von der Erde aus insgesamt knapp 59 % der Mondoberfläche einsehbar (vgl. Animation 9.5).

9.5  Libration des Mondes (Quelle: https://commons.wikimedia.org/wiki/File:Lunar_libration_with_phase_Oct_2007_(continuous_loop).gif, 21.04.2022)

"Was wäre die Erde ohne den Mond" gehört zu den beliebtesten Gedankenexperimenten der Astronomie. Neben dem Faktum, dass es weder romantisch-helle Mondnächte noch Orientierungshilfen für nachtfliegende Insekten gäbe, hat der Mond weitaus tiefergreifendere Bedeutungen für unseren Planeten.
Zum einen bremst seine Anziehungskraft die Geschwindigkeit, mit der sich die Erde um sich selbst dreht; das heißt, der Mond bremst die Rotation der Erde. Ohne ihn wäre ein Tag nur etwa 8 Stunden lang, was zu katastrophalen Windverhältnisse wie auf den Großplaneten Jupiter oder Saturn führen würde.
Die Schwerkraft des Mondes hatte aber auch eine entscheidende Bedeutung für die Entstehung und Entwicklung des Lebens auf der Erde, wie kürzlich gerechnete Klimamodelle für die Erde ohne Mond zeigen. Dadurch entfällt dessen stabilisierende Wirkung für die Lage der Erdrotationsachse. Ohne Mond kann sie zwischen 0° und 85° schwanken. Wie der Planet Uranus könnte die Erde förmlich auf ihrer Bahn um die Sonne entlang rollen. Tropische Zonen versänken dann unter einer Schneedecke, und die Polregionen würden sich auf bis zu 80°C erhitzen. Kontinente in den "gemäßigten" Breiten wären enormen Temperaturschwankungen zwischen −25 °C und +45 °C binnen weniger Monate ausgesetzt. Bei einer anderen Lage der Kontinente - vor 200 Millionen Jahren gab es ja nur den großen Superkontinent Pangea auf unserem Planeten - wären die Bedingungen noch extremer.
Dazu kommt, dass der Mond für die Gezeiten verantwortlich ist. Das beständige Wechseln zwischen sowohl trockenen und feuchten, als auch salzarmen und salzreichen Umweltverhältnissen begünstigte die Entstehung des Lebens wesentlich. Ohne den Mond hätte sich das irdische Leben also – wenn überhaupt – völlig anders entwickelt.

Die Gezeiten

9.6  Bay of Fundy
(Quelle: "File:Bay of Fundy Low Tide.jpg" by Samuel Wantman is marked with CC BY-SA 3.0,
https://wordpress.org/openverse/image/d45908d8-1582-406e-a0d5-846c638816b5, 21.04.2022,
"File:Bay of Fundy High Tide.jpg" by Samuel Wantman is marked with CC BY-SA 3.0,
https://wordpress.org/openverse/image/6776a81b-6bf7-41df-9e6c-bf4916d7408a, 21.04.2022)

In der Bay of Fundy im Osten Kanadas schwankt der Wasserstand regelmäßig über 15 m (vgl. Abbildung 9.6). Ein solches periodisches Auf- und Ablaufen des Wassers an den Meeresküsten nennen wir Gezeiten. Unter Flut verstehen wir das ansteigende Wasser vom Niedrig- bis zum Hochwasser. Mit Ebbe bezeichnen wir das Fallen des Wassers. Der Verlauf von einem Niedrigwasser zum nächsten wird Tide genannt. Er dauert im Mittel 12 Stunden und 25 Minuten. Folglich verschiebt sich das Niedrigwasser an einem Ort von Tag zu Tag um etwa 50 Minuten.
Eine naheliegende Ursache für die Gezeiten ist die Gravitationskraft des Mondes, welche die Wassermassen der Weltmeere zum Mond hinzieht. Bei dieser Theorie stößt man jedoch auf eine Schwierigkeit: Zwischen Mondaufgang und Mondaufgang liegen nicht einmal Ebbe und Flut, sondern zweimal (vgl. Animation 9.7 - nicht maßstabgetreu).

9.7  Wechsel von Ebbe und Flut (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022, Icons erstellt von Freepik, https://www.flaticon.com/de/kostenloses-icon/leuchtturm_1064780, 20.04.2022)

Der Grund für dieses Problem liegt darin, dass wir immer wieder glauben, dass die Erde der Mittelpunkt des ganzen Geschehens ist. Tatsächlich jedoch rotiert der Mond nicht um den Mittelpunkt der Erde; vielmehr bewegen sich Erde und Mond um ihren gemeinsamen Massenschwerpunkt, der wegen der relativ großen Masse der Erde im Vergleich zum Mond noch im Innern unseres Planeten liegt (vgl. Animation 9.8 - nicht maßstabgetreu).

9.8  Rotation der Erde und des Mondes um den Massenschwerpunkt (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

Für die folgenden Überlegungen wird das Bezugssystem gewählt, in welchem der gemeinsame Massenschwerpunkt ruht. Der Mittelpunkt Erde bewegt sich auf einem Kreis um diesen gemeinsamen Massenschwerpunkt. Im Erdmittelpunkt hält sich die dadurch hervorgerufene Zentrifugalkraft mit der Gravitationskraft des Mondes die Waage. Wie die folgende Animation 9.9 zeigt, bewegen sich damit auch alle weiteren Erdpunkte auf Kreisbahnen, die den gleichen Radius besitzen. In allen diesen Punkten wirkt also die gleiche Zentrifugalkraft wie im Mittelpunkt.

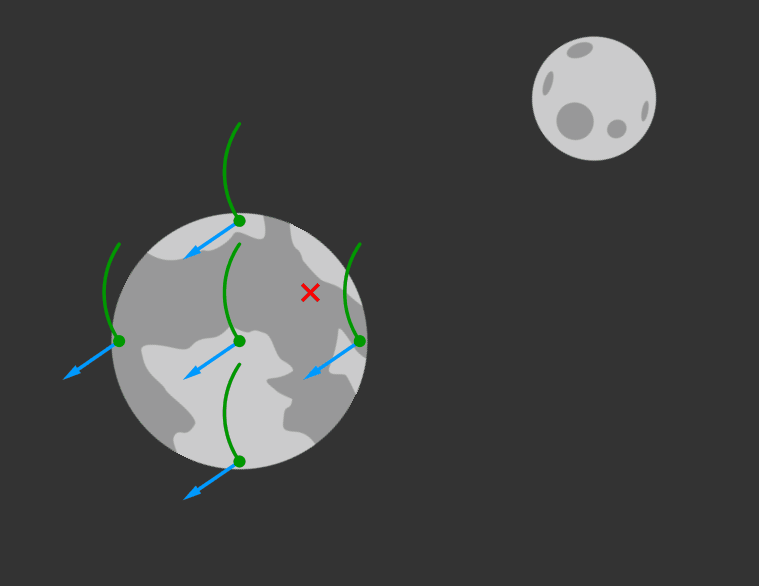
9.9  Rotation der Erde und des Mondes um den Massenschwerpunkt (Quelle: Icons erstellt von Alfredo Hernandez, https://www.flaticon.com/de/kostenloses-icon/globus_494445, 08.03.2022)

In der folgenden Abbildung 9.10 (nicht maßstabgetreu) ist die Zentrifugalkraft im Mittelpunkt der Erde und in Punkten auf der Erdoberfläche mit grüner Farbe eingezeichnet. Sie ist für jeden Punkt auf (und in) der Erde gleich groß und verläuft immer parallel zur Richtung vom Mondmittelpunkt zum Erdmittelpunkt. Im Gegensatz zur Zentrifugalkraft ist die durch den Mond verursachte Gravitationskraft (blau) je nach Entfernung zum Mond unterschiedlich groß. Sie zeigt immer zum Mondmittelpunkt und nimmt mit der Entfernung zum Mond ab. Nur im Erdmittelpunkt ist sie gegengleich zur Zentrifugalkraft. Durch Kräfteaddition erhalten wir die Gesamtkräfte (rot), welche für die Gezeitenentstehung verantwortlich sind. Sie verursachen ein Anheben (Flut) und ein Absinken (Ebbe) der Wassermassen.

9.10  Zentrifugalkraft, Gravitationskraft des Mondes, Gezeitenkraft

Die Erde dreht sich während einer siderischen Mondperiode (das sind 27,321662 Tage und demnach 27,396495 Sterntage) rund 27,396495-mal um ihre Achse. Jeder Punkt der Erde wird daher in dieser Zeit 2 · 26,396495-mal in das Flutgebiet und ebenso oft in das Ebbegebiet gelangen. Ebbe und Flut werden daher in Intervallen von 27,321662 Tagen : (4 · 26,396495) = 6,21 Stunden aufeinanderfolgen. Eine ganz gleichartige Wirkung übt die Sonne aus. Sie kann die Wirkung des Mondes unterstützen (Springflut) oder schwächen (Nippflut).
Die tatsächlichen Verhältnisse sind sehr kompliziert. Größte Flut tritt nicht genau an der dem Mond nächstliegenden und der gegenüberliegenden Stelle der Erde auf. Die geographischen Verhältnisse haben großen Einfluss. Da Ebbe und Flut während einer Erddrehung gleichsam über die Erde hinwegwandern, haben sie beträchtliche Wasserströmungen zur Folge. Durch die dabei auftretende Reibung wird die Rotationsenergie der Erde vermindert und damit ihre Achsendrehung verlangsamt.

Die Roche-Grenze

Auch die Erde übt auf den Mond Gezeitenkräfte aus. Ein Massenpunkt μ auf der der Erde zugewandten Seite der Mondoberfläche ist der Erde rund 1737 km (Mondradius) näher als der Mondmittelpunkt. Dadurch erfährt dieser Massenpunkt eine größere Gravitationskraft als ein Massenpunkt im Mondschwerpunkt. Die Differenz dieser beiden Kräfte bewirkt eine Gezeitenkraft.
Betrachten wir im Folgenden einen Planeten der Masse M und einen Mond der Masse m (vgl. Abbildung 9.11).

9.11  Gezeitenkraft eines Planeten auf einen Mond

Dabei gilt, wenn man die Kräfte auf eine Probemasse μ betrachtet

Falls der Radius des Mondes sehr viel kleiner als der Abstand der beiden Objekte ist, d.h.

so lässt sich obiger Ausdruck zu

vereinfachen. Durch die Gezeitenkraft wird der Mond vom Planeten in die Länge gezogen. Käme der Mond dem Planeten näher, so würde irgendwann die Gezeitenkraft größer werden als die Gravitationskraft, mit welcher die Probemasse μ an der Mondoberfläche "festgehalten" wird. Der Mond würde also "zerrissen" werden. Dieser Vorgang passiert mit einem Körper der Masse m allgemein dann, wenn die Gezeitenkraft auf die an der Oberfläche von m liegenden Masse μ erzeugt durch M gleich groß wird wie die Gravitationskraft von m auf dieselbe Masse. Das lässt sich so schreiben.

Aufgelöst nach dem kritischen Abstand d erhalten wir

Drücken wir nun noch die Massen durch die entsprechenden Volumina und Dichten aus

bzw.

so erhalten wir schließlich

Diesen Abstand nennt man Roche-Grenze, benannt nach dem französischen Astronomen und Mathematiker Édouard Albert Roche (1820 – 1883). Ist der Abstand eines Körpers kleiner als seine entsprechende Roche-Grenze, so wird er von den Gravitationskräften des größeren Himmelskörpers zerrissen. Für unseren Mond erhält man bezüglich der Erde eine Roche-Grenze von

Der Erdmond befindet sich also in sicherer Entfernung.

Bei obiger Herleitung haben wir angenommen, dass der betroffene Trabant fest ist und nur von den eigenen Gravitationskräften zusammengehalten wird (d.h. seine mechanische Festigkeit vernachlässigbar ist). Für reale Festkörper ist diese Annahme umso besser erfüllt, je größer der Körper ist. Daher können z.B. künstliche Satelliten problemlos auch innerhalb der Roche-Grenze kreisen, während große Objekte wie Monde dort nicht existieren können. Aus der obigen Formel erkennt man auch, dass die Roche-Grenze eines starren Körpers für Satelliten, deren Dichte mehr als doppelt so hoch ist wie die Dichte des Hauptkörpers, innerhalb des Hauptkörpers liegt. Dieser Fall tritt z.B. bei vielen felsigen Monden der Gasriesen unseres Sonnensystems auf. Solche Satelliten werden also auch bei nächster Annäherung an den Hauptkörper nicht durch dessen Gezeitenkräfte zerrissen. Ist der Trabant hingegen flüssig, so setzt er seiner Verformung keinen oder nur einen sehr geringen Widerstand entgegen. Er wird deshalb schon viel früher auseinandergezogen. Die Roche-Grenze verdoppelt sich dann etwa.

9.12  Saturn
(Quelle: https://solarsystem.nasa.gov/planets/saturn/overview/, 10.03.2022)

Die Abbildung 9.12 zeigt den Planeten Saturn und sein Ringsystem aufgenommen von der NASA-Sonde Cassini. Man geht davon aus, dass ein Teil der Ringe des Saturn entstanden ist, als ihm ein Mond zu nahe kam und von den Gezeitenkräften zerrissen wurde.

Literatur:
Höfling, Oskar: Physik - Lehrbuch für Unterricht und Selbststudium, 15. Aufl., Ferd. Dümmlers Verlag, Bonn 1987
Westphal, Wilhelm H.: Physik, 25./26. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1970
Gerthsen, Christian / Kneser, Hans Otto / Vogel, Helmut: Physik, 14. Aufl., Springer-Verlag, Berlin · Heidelberg · New York 1982
Tipler, Paul A. / Mosca, Gene: Physik für Wissenschaftler und Ingenieure, 6. Aufl., Spektrum Akademischer Verlag, Heidelberg 2009
Dobson, Ken / Grace, David / Lovett, David: Physics, Published by HarperCollinsPublishers Limited, London 2002
Schreiner, Josef: Lehrbuch der Physik 1. Teil, 2. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1969
Schreiner, Josef: Lehrbuch der Physik 2. Teil, 1. Aufl., Verlag Hölder-Pichler-Tempsky, Wien 1964